Похожие презентации:
Лекция 12. Интегрирование рациональных дробей, иррациональных дробей, тригонометрических функций
1.
Лекция 122.
Классрациональных
представить в виде дроби
функций
можно
P( x)
Q( x)
где P(x) и Q(x) – многочлены.
Если степень числителя не меньше степени
знаменателя, то дробь считается неправильной
и делением в ней выделяется целая часть.
3.
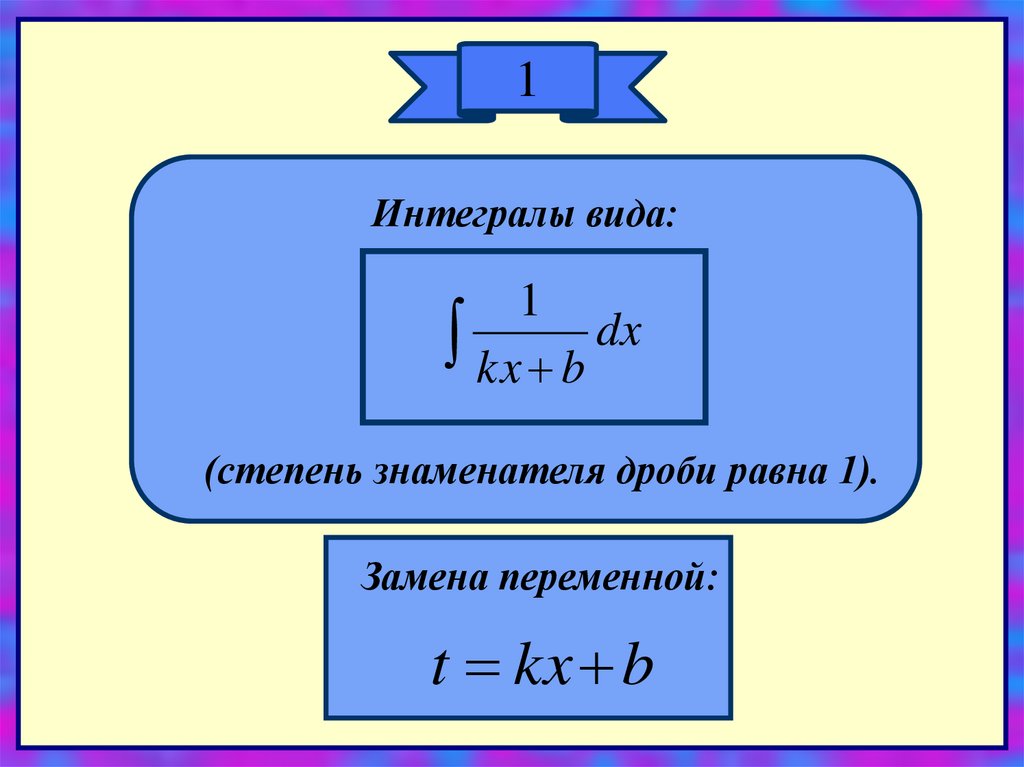
1Интегралы вида:
1
kx b dx
(степень знаменателя дроби равна 1).
Замена переменной:
t kx b
4.
Вычислить интеграл:1
1 2 x dx
5.
1 2x t1
1
1 1
1 2 x dx x 2 (t 1) 2 t dt
1
dx dt
2
1
1
ln t C ln 1 2 x C
2
2
6.
2Интегралы вида:
1
(kx b)n dx
(где n>1 – целое число).
Замена переменной:
t kx b
7.
Вычислить интеграл:1
(2 x 3)4 dx
8.
2x 3 t1
1
1 1
(2 x 3) 4 dx x 2 (t 3) 2 t 4 dt
1
dx dt
2
1 1
1
1
3 C
C
3
2 3t
6 (2 x 3)
9.
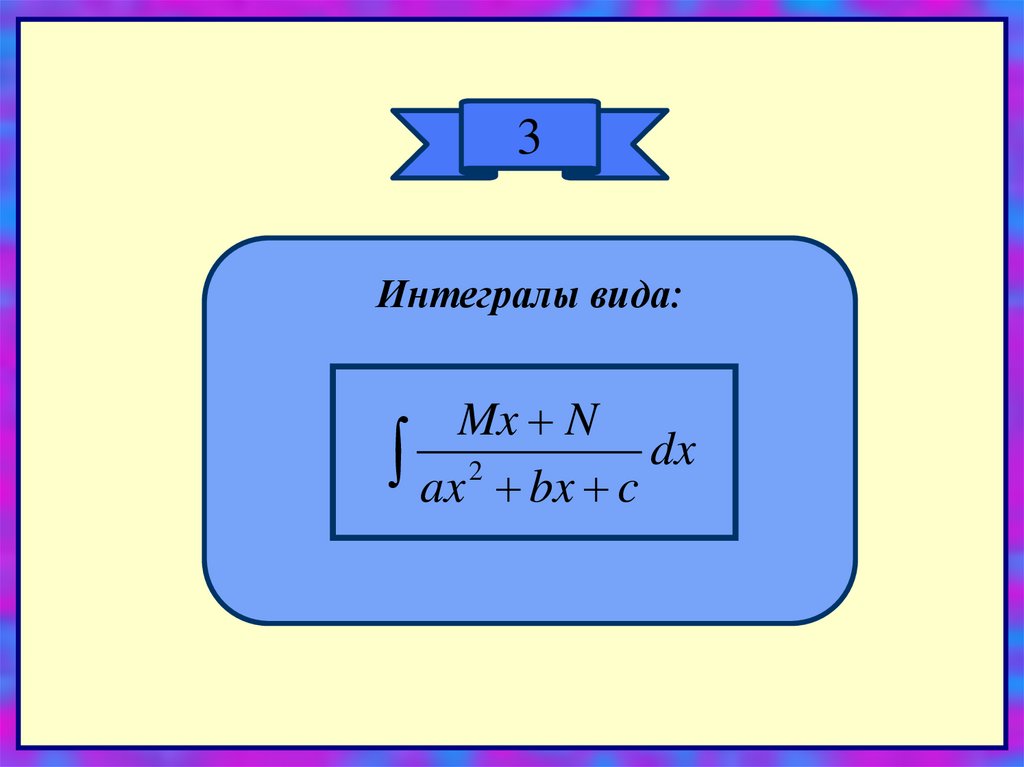
3Интегралы вида:
Mx N
ax 2 bx c dx
10.
В знаменателе дроби выделяется полный квадрати делается линейная замена переменной, так что
интеграл сводится к виду:
Mx N
x
1
ex 2 f dx M ex 2 f dx N ex 2 f dx
Для нахождения
замена:
1
первого
интеграла
2делается
t ex f
2
Тогда
ex f t
x
1 1
ex 2 f dx dt 2exdx 2e t dt
2
11.
11
ln t C
ln ex 2 f C
2e
2e
Второй интеграл при e f 0
сводится к табличному:
1
1
x
a 2 x 2 dx a arctg a C
а при
e f 0
сводится к табличному:
1
1
x a
x 2 a 2 dx 2a ln x a C
12.
1Вычислить интеграл:
x 1
4 x 2 4 x 3 dx
13.
x 1x 1
4 x 2 4 x 3 dx (2 x 1) 2 4 dx
2x 1 t
dt 2dx
1
1
t 1
1
2
2
dt
2
t 4
2
1 t 1
1
t
1
1
2
dt 2
dt 2
dt
4 t 4
4 t 4
4 t 4
1 1
1
t 2
du
ln
8 u
16 t 2
du 2tdt
t2 4 u
14.
11
t 2
ln u
ln
C
8
16
t 2
1
1
t 2
2
ln t 4
ln
C
8
16 t 2
1
1 2x 1 2
2
ln (2 x 1) 4 ln
C
8
16 2 x 1 2
1
1
2x 1
2
ln 4 x 4 x 3 ln
C
8
16 2 x 3
15.
2Вычислить интеграл:
2x 1
x 2 2 x 5 dx
16.
2x 12x 1
dx
dx
2
2
x 2x 5
( x 1) 4
x 1 t
2t 2 1
dt
2
dt dx
t 4
t
1
2t 1
dt 2
dt
2
dt 2 2
t 4
t 4
t 4
1
1
t
du arctg
u
2
2
du 2tdt
t2 4 u
17.
1t
ln t 4 arctg C
2
2
1
t
ln u arctg C
2
2
2
1
x 1
ln ( x 1) 4 arctg
C
2
2
1
x 1
2
ln x 2 x 5 arctg
C
2
2
2
18.
4Метод неопределенных коэффициентов
Рассмотренный выше способ вычисления
интегралов от рациональных дробей не
обобщается на случай, если степень
знаменателя больше двух.
В
этом
случае
используется
неопределенных коэффициентов.
метод
19.
Этотметод
связан
с
подынтегральной дроби
простых дробей.
представлением
в виде суммы
Для этого знаменатель дроби раскладывается
на множители.
Каждому типу множителя в знаменателе
отвечает в разложении простая дробь
некоторого вида.
20.
1Каждому неповторяющемуся множителю
вида (x-a) отвечает в разложении
простая дробь вида
A
x a
21.
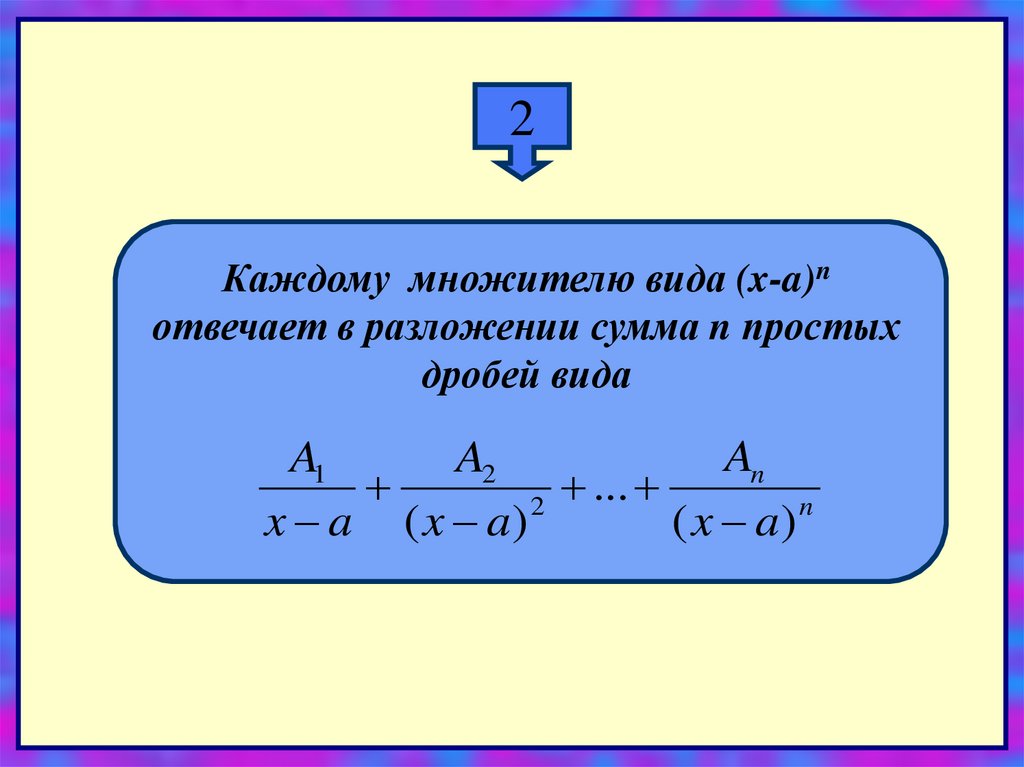
2Каждому множителю вида (x-a)n
отвечает в разложении сумма n простых
дробей вида
An
A1
A2
...
2
n
x a ( x a)
( x a)
22.
3Каждому неповторяющемуся множителю
вида (x2+px+q) отвечает в разложении
простая дробь вида
Mx N
x 2 px q
23.
4Каждому множителю вида (x2+px+q)k
отвечает в разложении сумма k простых
дробей вида
M k x Nk
M 1 x N1
M 2 x N2
2
... 2
2
2
k
x px q ( x px q)
( x px q)
24.
Вычислить интеграл:x 2x 2
x( x 2)( x 4) dx
2
25.
A3x 2x 2
A1
A2
x( x 2)( x 4)
x x 2 x 4
2
A1 ( x 2)( x 4) A2 x( x 4) A3 x( x 2)
x( x 2)( x 4)
26.
A1 ( x 2)( x 4) A2 x( x 4) A3 x( x 2)x 2x 2
2
При
x 0
1
A1
4
A1 ( 2) 4 2
При
x 2
A2 2(2 4) 2 2 2 2
2
При
x 4
A3 ( 4)( 6) 16 ( 8) 2
1
A2
6
13
A3
12
27.
x2 2x 21
1
13
x( x 2)( x 4)
4 x 6( x 2) 12( x 4)
x 2x 2
x( x 2)( x 4) dx
2
1 1
1
1
13
1
dx
dx
dx
4 x
6 x 2
12 x 4
1
1
13
ln x ln x 2 ln x 4 C
4
6
12























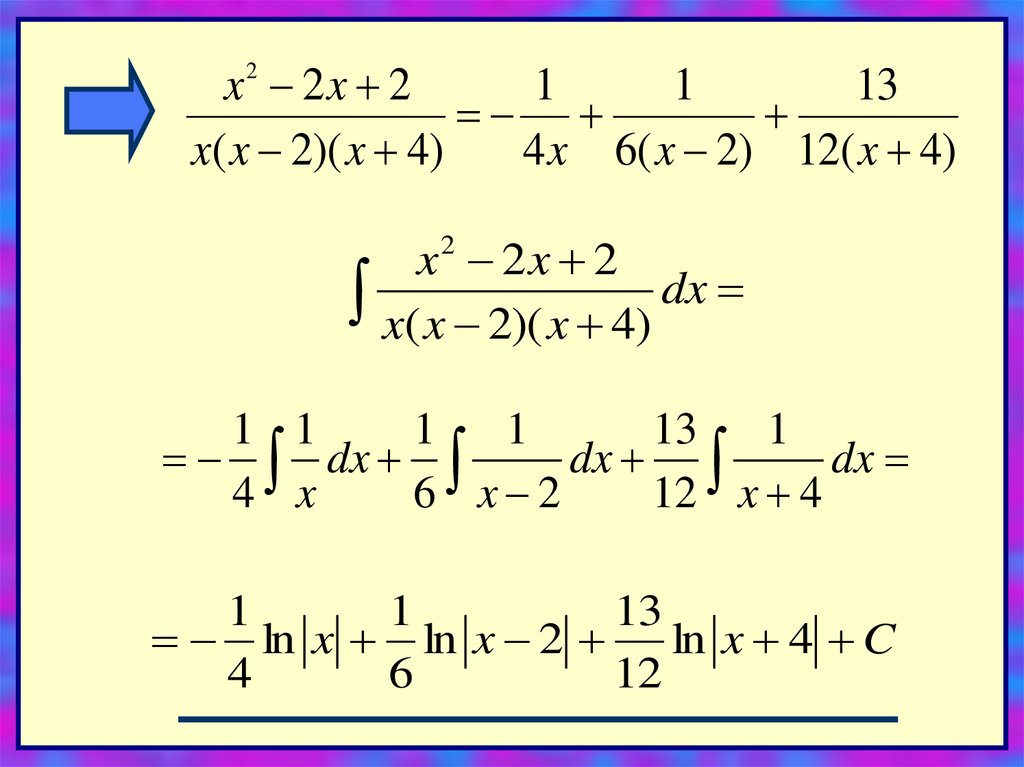
 Математика
Математика








