Теорія ймовірностей, ймовірнісні процеси і математична статистика

1.

Теорія ймовірностей,
ймовірнісні процеси і
математична статистика
7,8 ПЗ. НЕПЕРЕРВНІ ВИПАДКОВІ ВЕЛИЧИНИ:
Тема 1. Числові характеристики.
Тема 2. Закони розподілу.

2.

Определение непрерывной случайной величины
Случайной называется величина, которая принимает в
результате испытания то или иное (но при этом только одно)
возможное значение, заранее неизвестное, меняющееся от
испытания к испытанию и зависящее от случайных
обстоятельств.
Непрерывными называются случайные величины, которые могут
принимать любые значения из некоторого конечного или
бесконечного интервала.

3.

Определение функции распределения
Функция распределения случайной величины F(x) определяет
вероятность того, что случайная величина X примет значение,
меньше фиксированного действительного числа x, т.е.
Функция F(x) также называется интегральной функцией
распределения или интегральным законом распределения.
Если случайная величина X принимает все значения на отрезке
[x1,x2], то функция распределения

4.

Определение плотности вероятности
Плотностью вероятности (плотностью распределения,
дифференциальной функцией) f(x) непрерывной случайной
величины X называется первая производная от интегральной
функции F(x), т.е.
Для дискретной случайной величины плотность вероятности
не определена.
Кривая, изображающая функцию плотности вероятности f(x)
называется кривой распределения.

5.

Свойства плотности вероятности
1.
2. Функция распределения непрерывной случайной величины Х может быть выражена через
интеграл
где
– функция плотности вероятности.
3. Площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице, т.е.
4. Вероятность того, что Х принимает значение в интервале (х1 ,х2), равна
5. Если случайная величина X принимает все значения на отрезке [x1,x2], то
причем

6.

Тема 1. Числові
характеристики
неперервної
випадкової величини

7.

Математическое ожидание
Математическое ожидание непрерывной случайной величины вычисляется по
формуле
где f(x) – функция плотности вероятности случайной величины и интеграл
сходится абсолютно.
Математическое ожидание непрерывной случайной величины X, значения
которой принадлежат отрезку [x1, x2], равно
Математическое
величины.
ожидание
характеризует
среднее
значение
случайной

8.

Дисперсия
Формулы для вычисления дисперсии непрерывной случайной величины:
или
Дисперсия непрерывной случайной величины X, возможные значения которой
принадлежат отрезку [x1, x2], равна
Дисперсия характеризует степень рассеяния значений случайной величины
относительно ее математического ожидания.

9.

Среднее квадратическое отклонение
Среднее
квадратическое
отклонение
арифметическому квадратному корню из дисперсии
равно

10.

Тема 2. Закони
розподілу
неперервної
випадкової величини

11.

Законы распределения непрерывной
случайной величины:
Равномерный
Нормальный
Показательный

12.

Равномерный закон распределения
Непрерывная случайная величина Х имеет равномерное
распределение на интервале (a, b), если плотность вероятности
f(x) на этом интервале постоянна, а вне интервала равна нулю, т.е.
График плотности f(x) для равномерного распределения имеет вид

13.

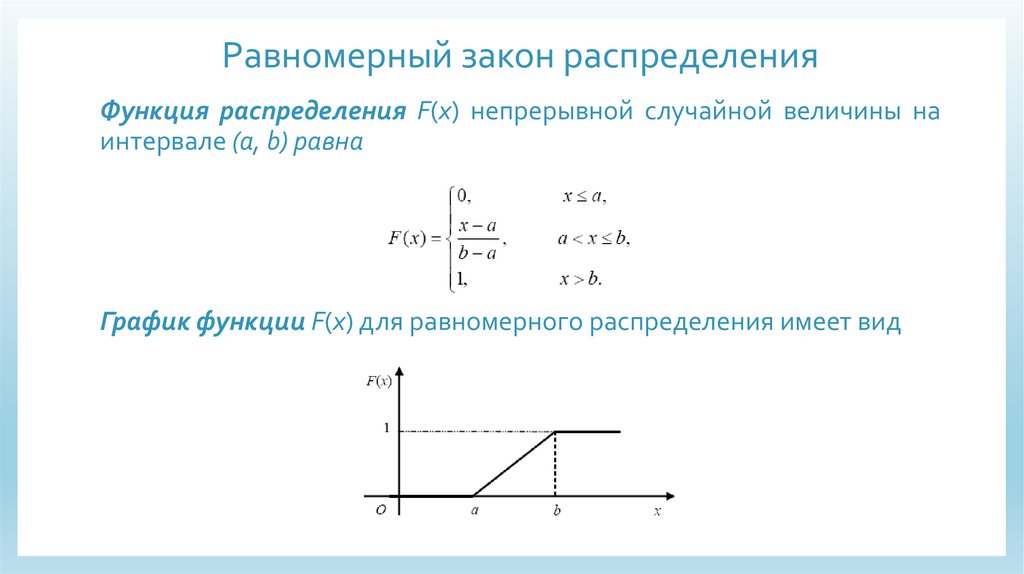
Равномерный закон распределения
Функция распределения F(x) непрерывной случайной величины на
интервале (a, b) равна
График функции F(x) для равномерного распределения имеет вид

14.

Равномерный закон распределения
Вероятность того, что значения случайной величины Х, имеющей
равномерное распределение, принадлежат интервалу (x1, x2) с [a, b],
определяется по одной из формул:

15.

Числовые характеристики случайной величины
математическое ожидание
дисперсия
среднее квадратическое отклонение
равномерное
распределение не имеет моды, а медиана равна
математическому ожиданию, то есть Me = M (X).

16.

Нормальный закон распределения
Если случайная величина X представляет собой сумму очень большого
числа взаимно независимых случайных величин, влияние каждой из
которых на всю сумму очень мало, то случайная величина X имеет
распределение, близкое к нормальному.
Непрерывная случайная величина с нормальным законом распределения
принимает любые значения в интервале
и может быть задана
плотностью вероятности f(x)
или функцией распределения F(х):
где μ и σ – параметры нормального распределения, Ф –функция Лапласа.

17.

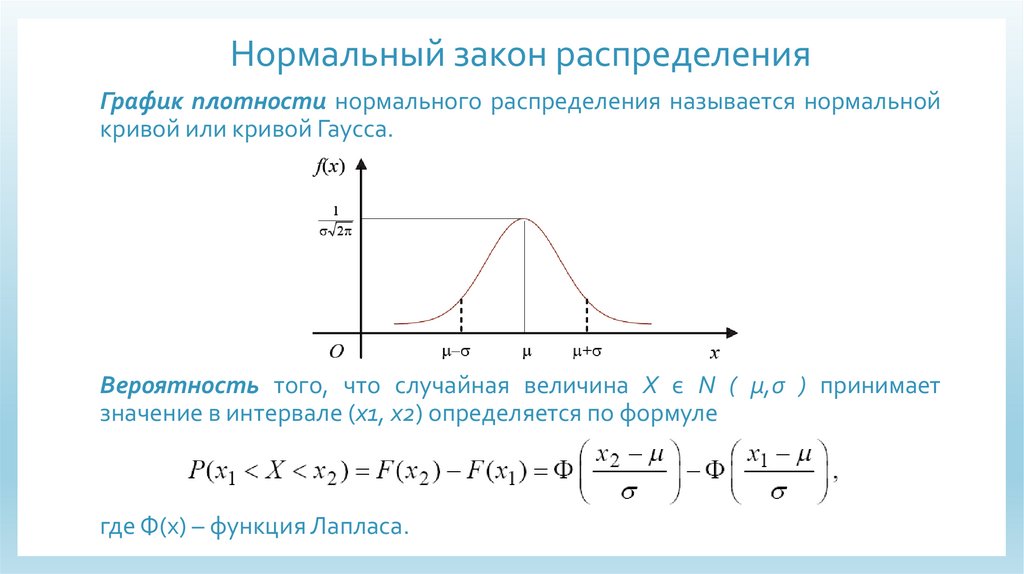
Нормальный закон распределения
График плотности нормального распределения называется нормальной
кривой или кривой Гаусса.
Вероятность того, что случайная величина X є N ( μ,σ ) принимает
значение в интервале (x1, x2) определяется по формуле
где Ф(х) – функция Лапласа.

18.

Числовые характеристики случайной величины
Параметрами нормального распределения являются
числовые характеристики случайной величины X, а именно:
математическое ожидание M (X) = μ ,
среднее квадратическое отклонение σ (X) = σ .
тогда дисперсия D (X) = σ2 .
Для нормального распределения выполняется равенство
M (X) = Me = Mo = μ.
Утверждение, о том, что случайная величина Х имеет
нормальное распределение с параметрами μ и σ кратко
записывается так: X є N ( μ,σ ).

19.

Показательный закон распределения
Непрерывная случайная величина X называется распределенной по
показательному закон, если она может принимать только
неотрицательные значения, а плотность вероятности определяется
следующим образом:
где λ – параметр распределения, λ >0.
Интегральная функция показательного распределения имеет вид

20.

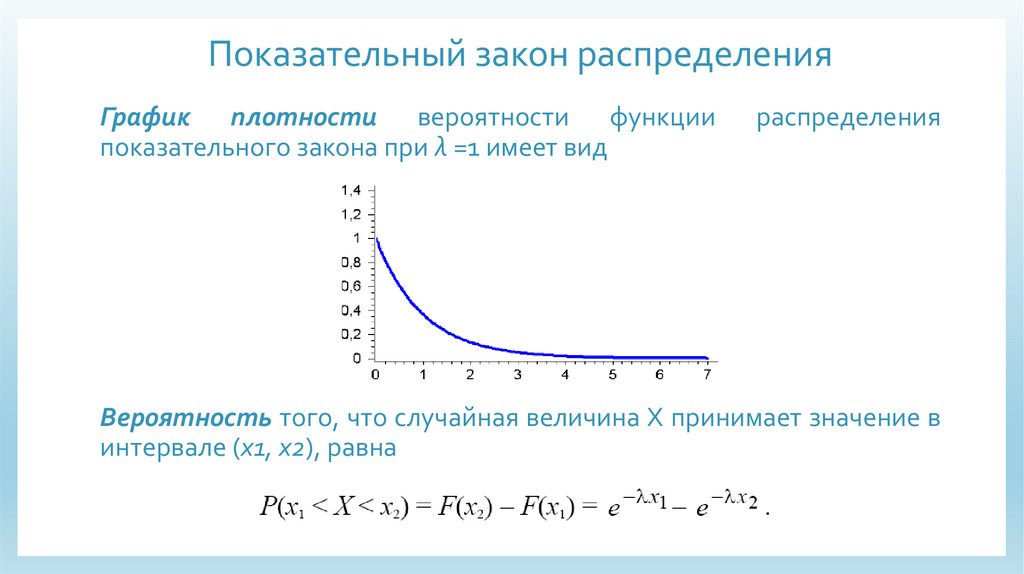
Показательный закон распределения
График плотности вероятности функции
показательного закона при λ =1 имеет вид
распределения
Вероятность того, что случайная величина Х принимает значение в
интервале (х1, х2), равна

21.

Числовые характеристики случайной величины
математическое ожидание
дисперсия
среднее квадратическое отклонение

22.

Задание
Самостоятельное решение типовых задач вручную* по вариантам из
списка
5 типовых задач
Решение индивидуальных задач вручную*
10 инд. задач по законам распределения (тема 8)
*графики лучше строить в Excel,
интегралы можно рассчитывать в MathCad
Контрольная работа по всем пройденным темам решается вручную
4 задачи
(3 из теста, 1 из методички – инд. зад. темы 7 по вариантам)