Урок 11. Функция распределения случайных величин

1. Урок 11

Функция распределения случайных
величин

2.

Для характеристики поведения НСВ
используют не вероятность события Р(Х=х), а
Р(Х<х), где х – некоторое фиксированное
число.
Если х изменяется, то изменяется и Р(Х<х), т.е.
Р(Х<х) является функцией.
Определение. Функцией распределения
случайной величины Х называется функция
F(x), задающая вероятность того, что
случайная величина Х<х, т.е. F(x)= Р(Х<х).
Эта функция называется интегральной
функцией распределения.

3. Построение интегральной функции распределения.

Х
х1
х2
х3
…
хn
Р
р1
р2
р3
…
рn
х х1 F ( х) P( x x1 ) 0
х1 x х2 F ( x) P( x x2 ) P( x x1 ) p1
x2 x x3 F ( x) P( x x3 ) P( x x1 ) P( x x2 ) p1 p2
...
xn 1 x xn F ( x) P( X xn ) p1 p2 ... pn 1
x xn F ( x ) 1

4. Задача 1.

Построить интегральную функцию распределения и ее график,
используя таблицу исходных данных:
Х
Р
x 1
1
0,1
3
0,2
4
0,2
5
0,3
F ( x) 0
1 x 3 F ( x) 0,1
3 x 4 F ( x) 0,1 0,2 0,3
4 x 5 F ( x ) 0,3 0,2 0,5
5 x 7 F ( x ) 0,5 0,3 0,8
7 x 8 F ( x) 0,8 0,1 0,9
x 8 F ( x ) 0,9 0,1 1
7
0,1
8
0,1

5.

График (коммулята)
x 1 F ( x) 0
1 x 3 F ( x) 0,1
3 x 4 F ( x) 0,1 0,2 0,3
4 x 5 F ( x) 0,3 0,2 0,5
5 x 7 F ( x) 0,5 0,3 0,8
7 x 8 F ( x) 0,8 0,1 0,9
x 8 F ( x) 0,9 0,1 1
F
1
0,9
0,8
*
*
*
0,5
*
0,3
0,1
*
*
1
3 4
5
7
8
Х

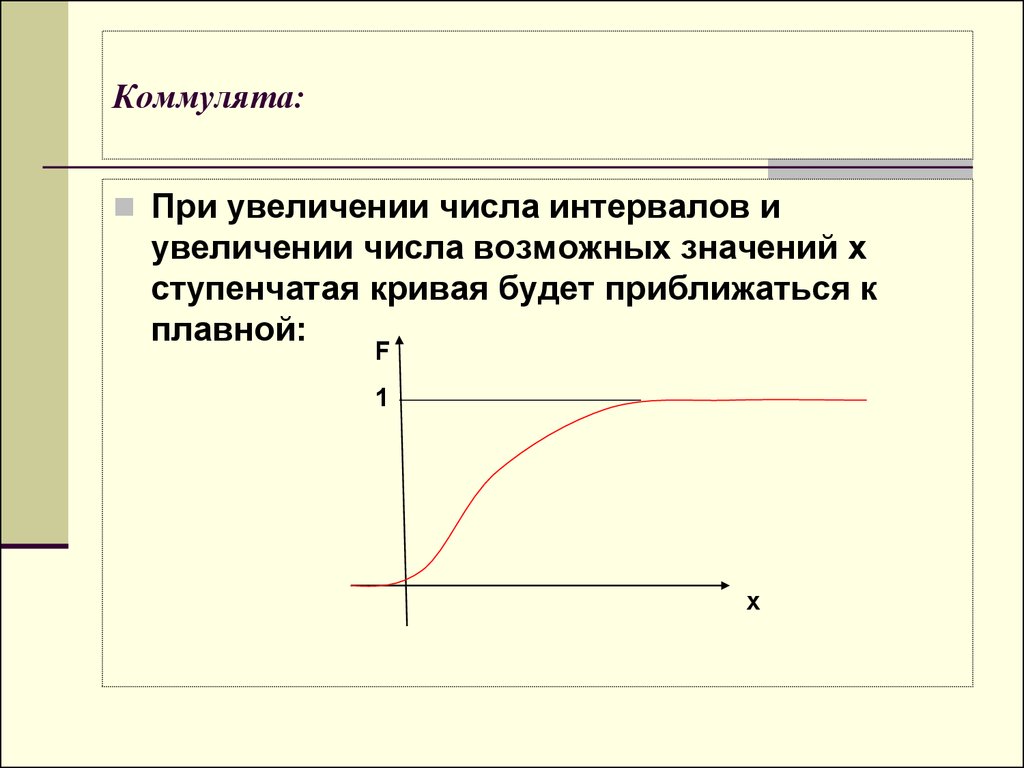
6. Коммулята:

При увеличении числа интервалов и
увеличении числа возможных значений х
ступенчатая кривая будет приближаться к
плавной:
F
1
х

7. Свойства интегральной функции распределения:

1.0 F ( x) 1
2.F ( x) неубывающая, т.е. P( x ) F ( ) F ( )
3. lim F ( x) 0;
lim F ( x) 1
x
x
4. P( ) 0, где отдельно взятое значение
непрерывной СВ : lim P( x ) F ( ) F ( ) 0
5. P ( x ) P ( x )

8. Задача 2.

Функция распределения СВ задана
выражением:
0
,
при
x
4
1
3
F ( x) a sin( x ) , при х
4
2
4
4
3
1, при х 4
Найти коэффициент а; вероятность попадания
3
) и построить
значения СВ в интервал ( ;
4 4
график.

9. Решение:

3
1
1.при х
F ( x) 1 a sin( x ) 1,
4
4 2
1
1
a sin , a .
2 2
2
3
3
1
1 1
1 1
2. P ( x ) F ( ) F ( ) sin sin 0
4
4
4
4
2
2 2 2
2 2

10.

3.
F
1
4
2
3
4
X

11. Плотность распределения вероятности

Используя интегральную функцию
распределения трудно судить о
характере распределения СВ в
небольшой окрестности точки на
числовой прямой.

12.

Пусть имеется НСВ с интегральной функцией
распределения F(x).
Рассмотрим вероятность попадания значений СВ на
участок ( х; х х )
Р ( х X x x) F ( x x) F ( x);
определим вероятность , которая приходится
на единицу длины этого участка :
Р ( х X x x) F ( x x) F ( x)
;
x
x
P ( x X x x)
F ( x x) F ( x)
lim
lim
?
x 0
x 0
x
x

13.

F ( x x) F ( x)
/
lim
F ( x) f ( x)
x 0
x
Дифференциальной функцией распределения
или плотностью распределения называется
первая производная интегральной функции
распределения.

14.

График:
f
Кривая распределения
1
x

15. Свойства дифференциальной функции распределения

1. Для любого х, f ( х) 0;
2. P ( x
3.
)
f ( x) dx;
f ( x) dx 1;
4. F ( x) x f (t ) dt ;
5.
f ( x) 1

16. Задача 3.

0, x 4 ,
1
3
1
F ( x ) sin( x ) ,
x
,
4
2 4
4
2
3
1, x 4
0, x 4 ,
3
1
/
F ( x ) f ( x ) cos( x ),
x
,
4 4
4
2
3
0, x 4

17. Графики:

F
f
1
1
2
4
3
4
x
4
3
4
x

18. Решить обратную задачу: составить интегральную функцию распределения по дифференциальной.

0, x 4 ,
3
1
f ( x) cos( x ), x
,
4
4
4
2
3
0, x 4
x
4
x
, F ( x) 0dx 0;