Похожие презентации:
Показникова функція
1.
Підготували:Рожкова Алла Анатоліївна, вчитель математики
ЗОШ № 2 м. Черкаси, І категорія
Бушина Інна Борисівна, вчитель математики та
інформатики, ЗОШ № 5, вища категорія, вчительметодист
2. Означення показникової функції
Функція y=ax , де a>0 і a≠1називається показниковою (з основою a).
Наприклад:
2) y 3
1) y 2,5 ;
x
1
3) y
7
3 x 1
;
x 2
;
4) y 3
cos x
.
3.
Які з наведених функцій є показниковими :2) y x 3 ;
1) y 3 ;
x
4) y ( 4) ;
x
5) y
201
3) y 1x ;
x 3
;
7) y x 5 ; 8) y 1 7 ;
8
10) y x x ;
11) y x ;
x
6) y x 0,6 ;
9) y 9 x ;
2
12) y
3
5 x
.
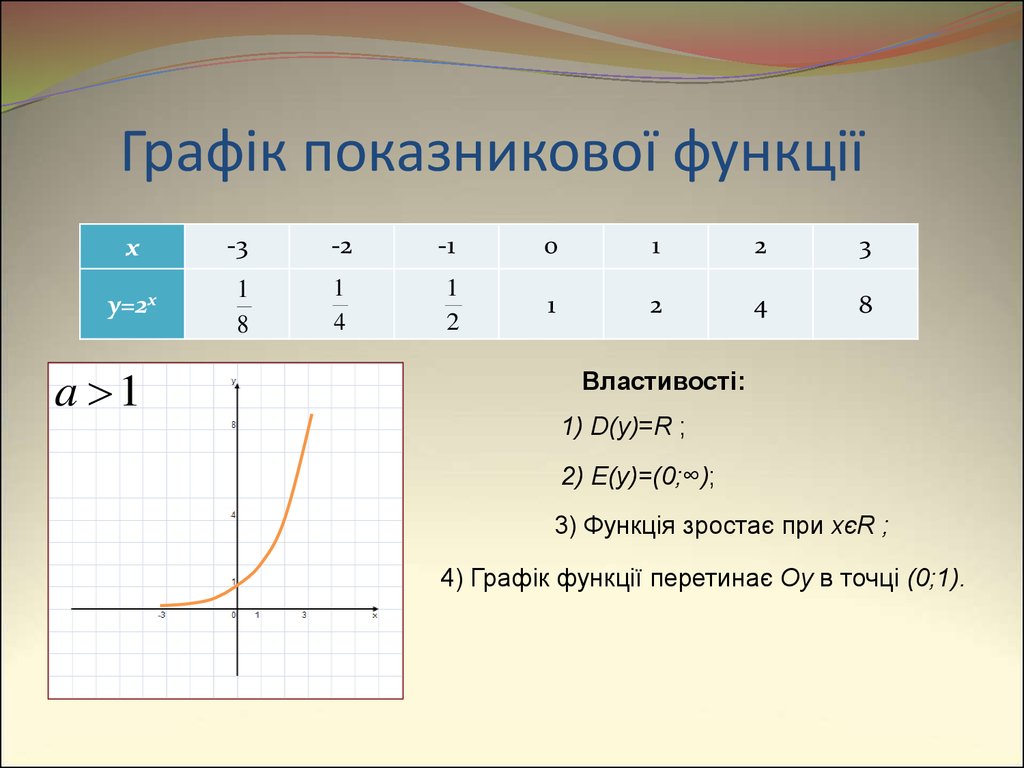
4. Графік показникової функції
x-3
-2
-1
0
1
2
3
y=2x
1
8
1
4
1
2
1
2
4
8
a 1
Властивості:
1) D(y)=R ;
2) E(y)=(0;∞);
3) Функція зростає при xєR ;
4) Графік функції перетинає Oy в точці (0;1).
5.
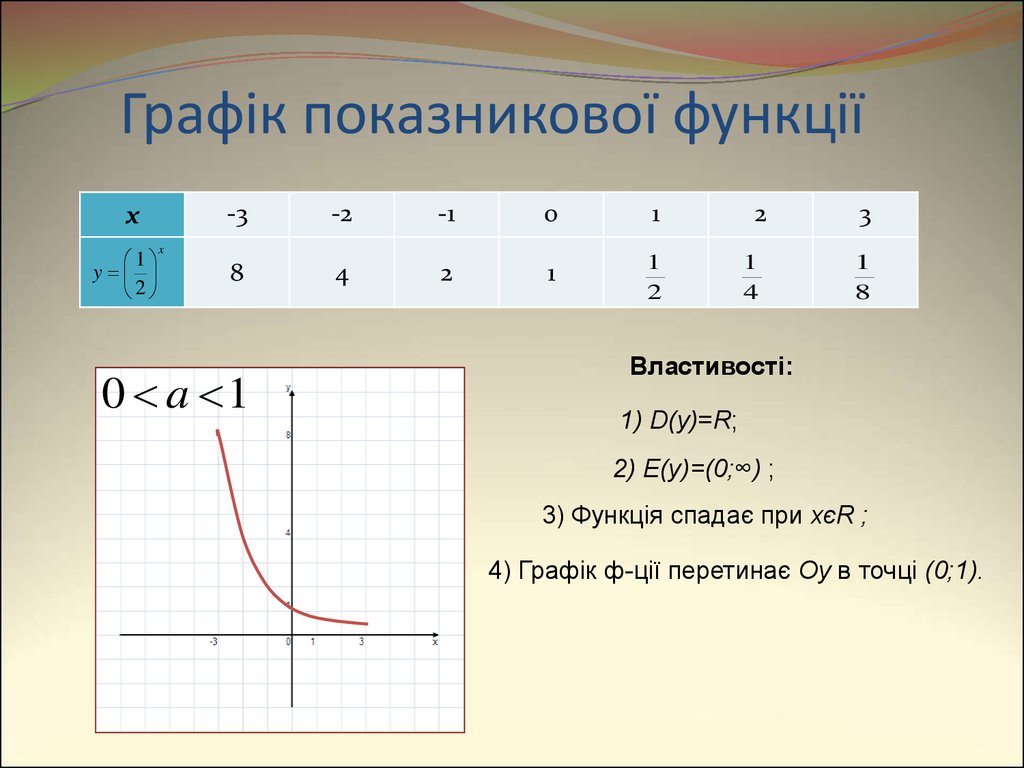
Графік показникової функціїx
1
y
2
-3
-2
-1
0
1
8
4
2
1
1
2
x
0 a 1
2
1
4
3
1
8
Властивості:
1) D(y)=R;
2) E(y)=(0;∞) ;
3) Функція спадає при xєR ;
4) Графік ф-ції перетинає Oy в точці (0;1).
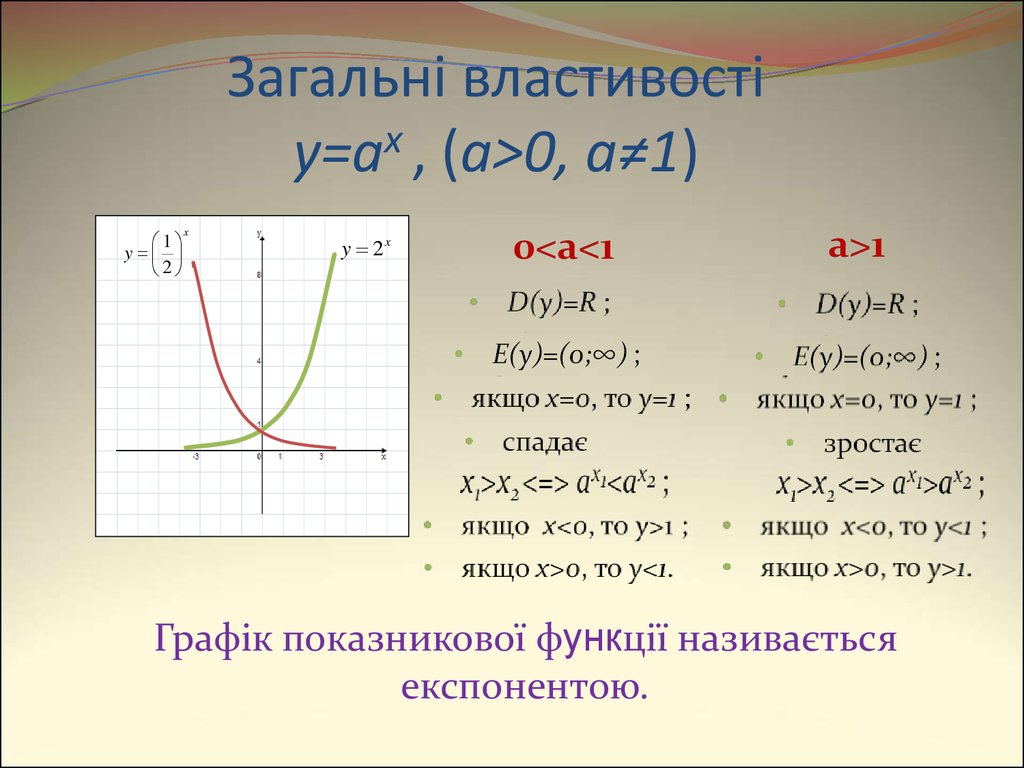
6. Загальні властивості y=ax , (a>0, a≠1)
Загальні властивостіx
y=a , (a>0, a≠1)
1
y
2
x
y 2x
Графік показникової функції називається
експонентою.
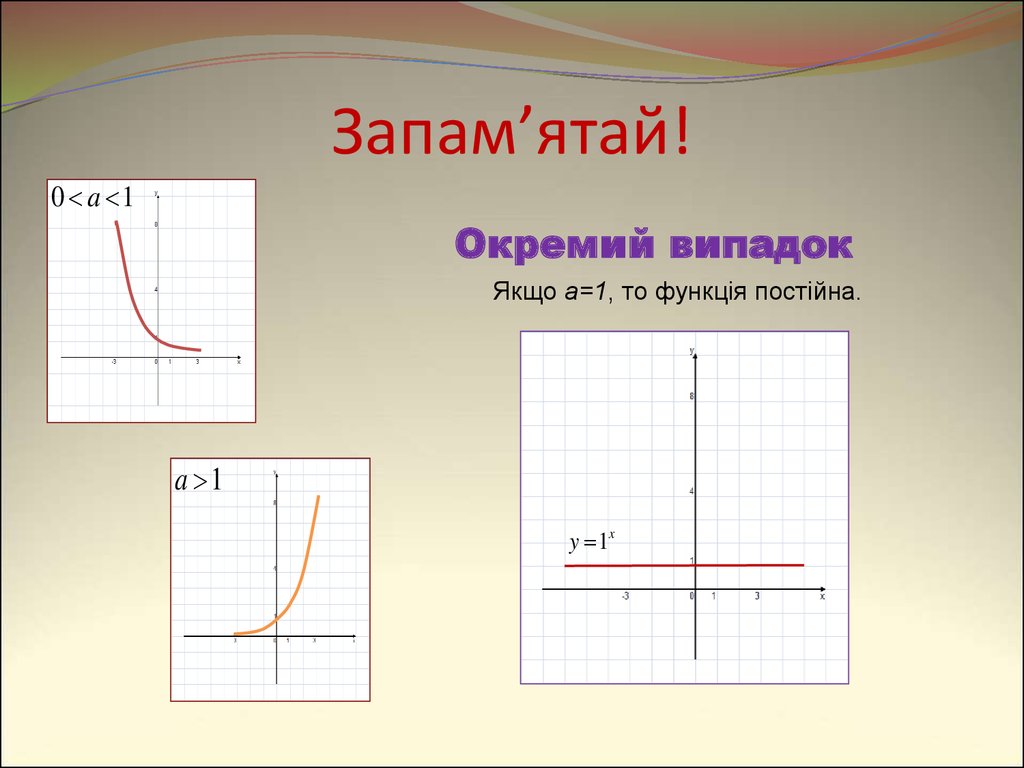
7. Запам’ятай!
0 a 1Окремий випадок
Якщо a=1, то функція постійна.
a 1
y 1x
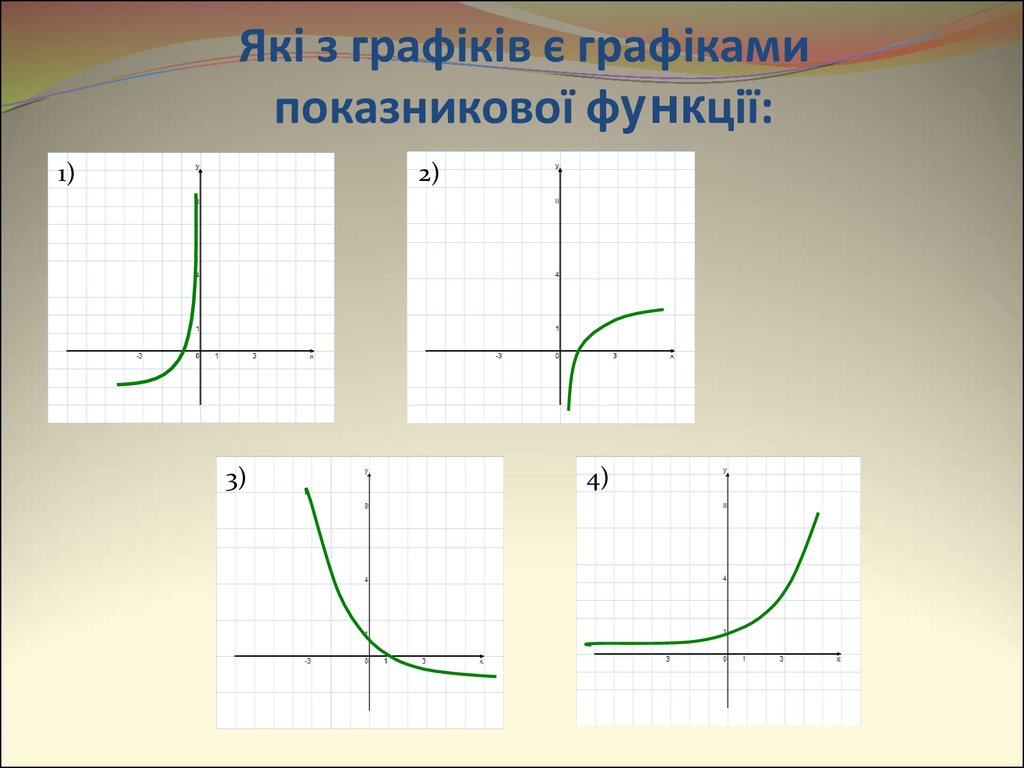
8. Які з графіків є графіками показникової функції:
1)2)
3)
4)
9. Застосування властивостей
Порівняти x і y, якщо:a) 0,3 0,3 (т.я. 0,3<1, то x<y);
x
б) 5x 5y
y
(т.я. 5>1, то x<y);
x
y
1
1
в)
3
3
(x>y).
Порівняти a з одиницею (a>0), якщо:
а) a7>a10
б) a-5<a-3
(функція y=at із зростанням
аргументу спадає, тому a < 1);
(із збільшенням показника степінь
збільшується, тому a > 1).
10. Виконайте:
1) Знайти область визначення ф-ції:1
в) y 13 x 2.
б) y 2 x ;
a) y 7 2x ;
2) Який висновок можна зробити щодо a (a>0), якщо:
а)a 0,3 1;
1
3
2
7
б )a a ;
2
в)a
3
1
1 1
; ;
3
3 3
2
1, 5
2
1 1
; ;
3 3
a 5.
3
3) Розташуйте числа
у порядку
зростання.
4) Порівняти x і y, якщо відомо, що вірна нерівність:
а)4 4 ;
x
y
б )15x 15 y ;
в ) 0,5 0,5 .
x
y
11.
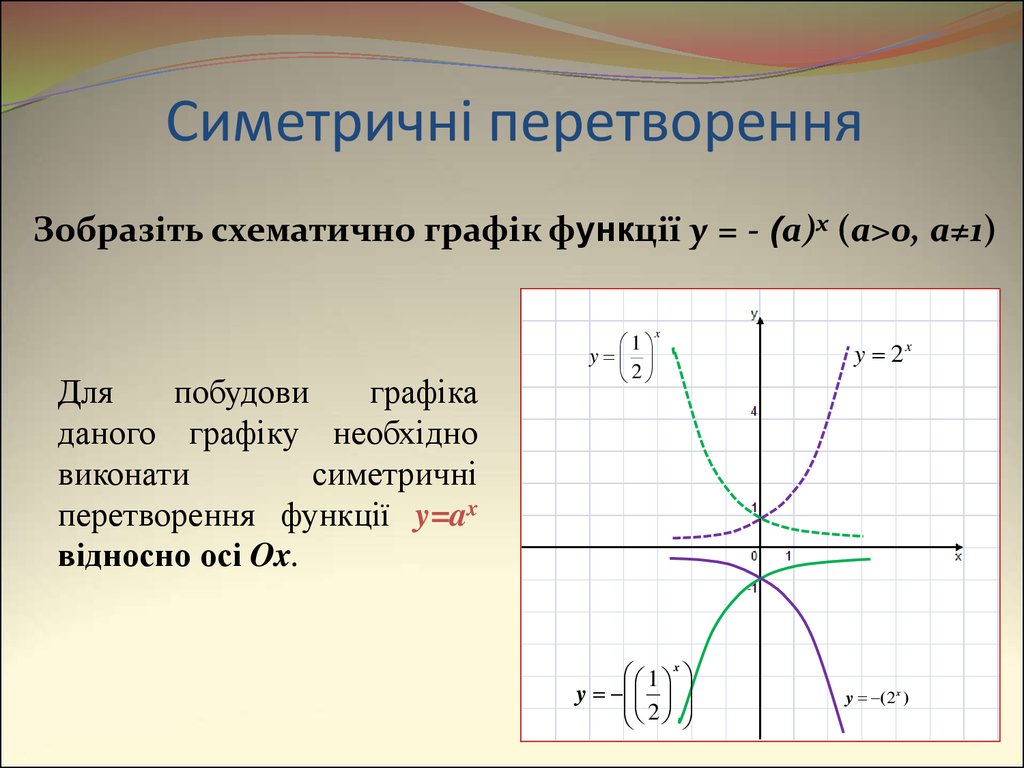
12. Симетричні перетворення
Зобразіть схематично графік функції y = - (a)x (a>0, a≠1)Для
побудови
графіка
даного графіку необхідно
виконати
симетричні
перетворення функції y=ax
відносно осі Ox.
1
y
2
x
1 x
y
2
y 2x
y (2 x )
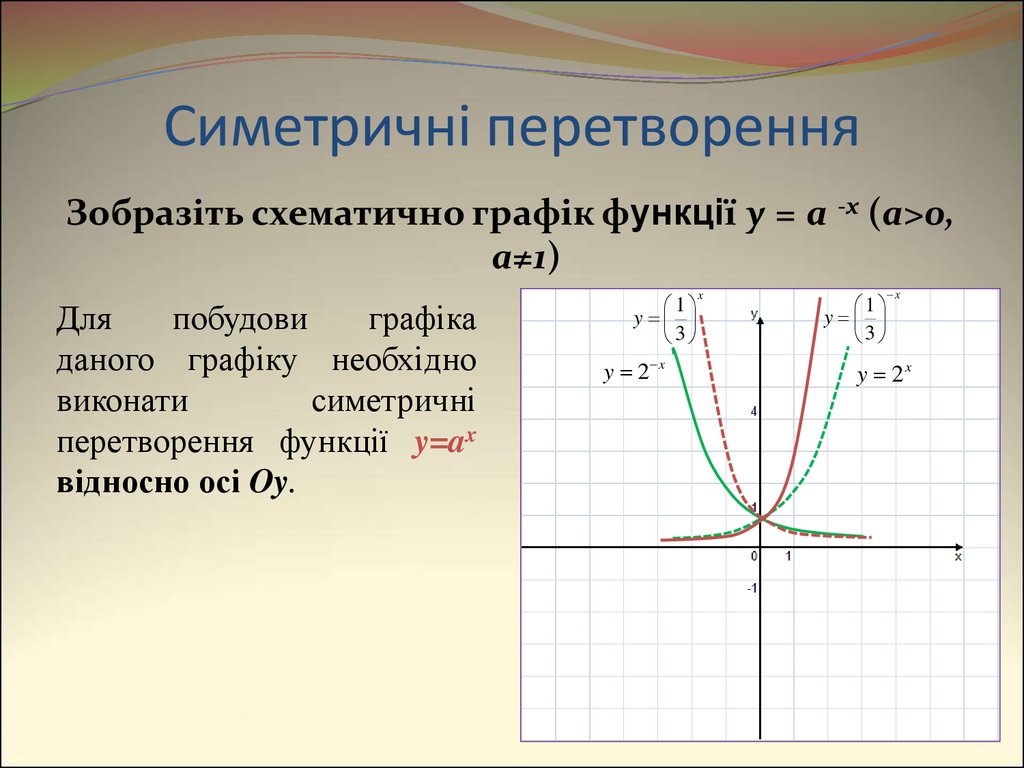
13. Симетричні перетворення
Зобразіть схематично графік функції y = a -x (a>0,a≠1)
Для
побудови
графіка
даного графіку необхідно
виконати
симетричні
перетворення функції y=ax
відносно осі Oy.
1
y
3
y 2 x
x
1
y
3
x
y 2x
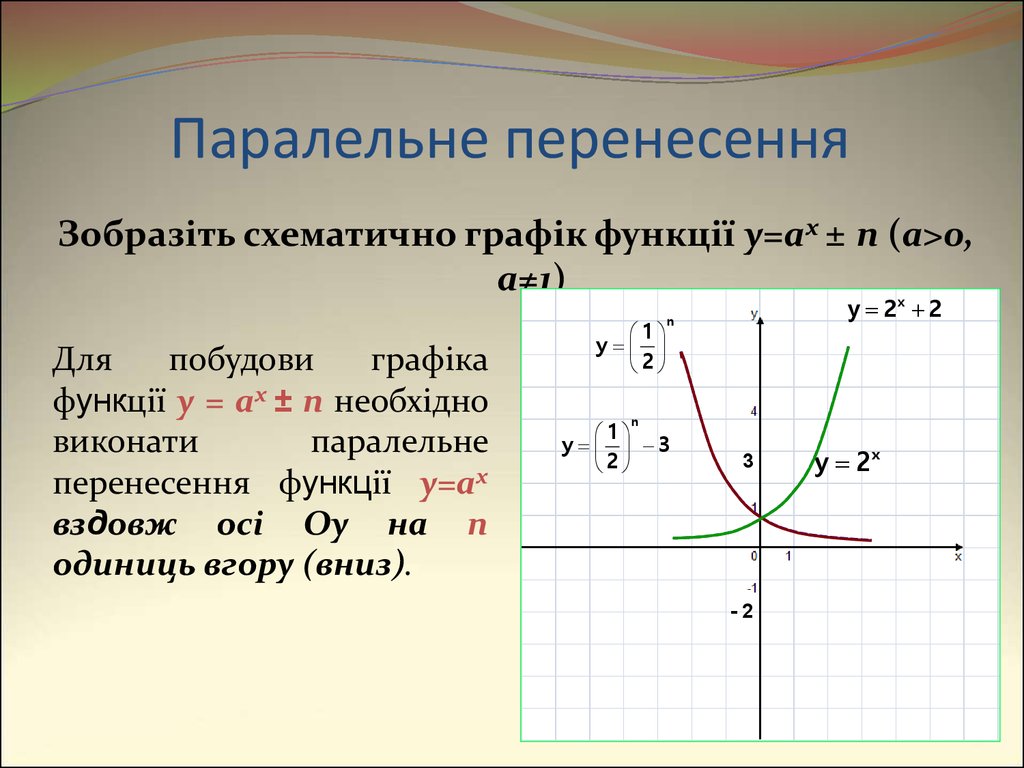
14. Паралельне перенесення
Зобразіть схематично графік функції y=ax ± n (a>0,a≠1)
Для
побудови
графіка
функції y = ax ± n необхідно
виконати
паралельне
перенесення функції y=ax
вздовж осі Oy на n
одиниць вгору (вниз).
1
y
2
y 2x 2
n
n
1
y 3
2
3
-2
y 2x
15.
Паралельне перенесенняЗобразіть схематично графік функції
y=a x ± m (a>0, a≠1)
1
y
2
Для побудови графіка
функції y = ax ± m необхідно
виконати
паралельне
перенесення функції y=ax
вздовж осі Ox на m
одиниць вліво (вправо).
1
y
2
x
y 2 x 3
y 2x
x 2
-2
3
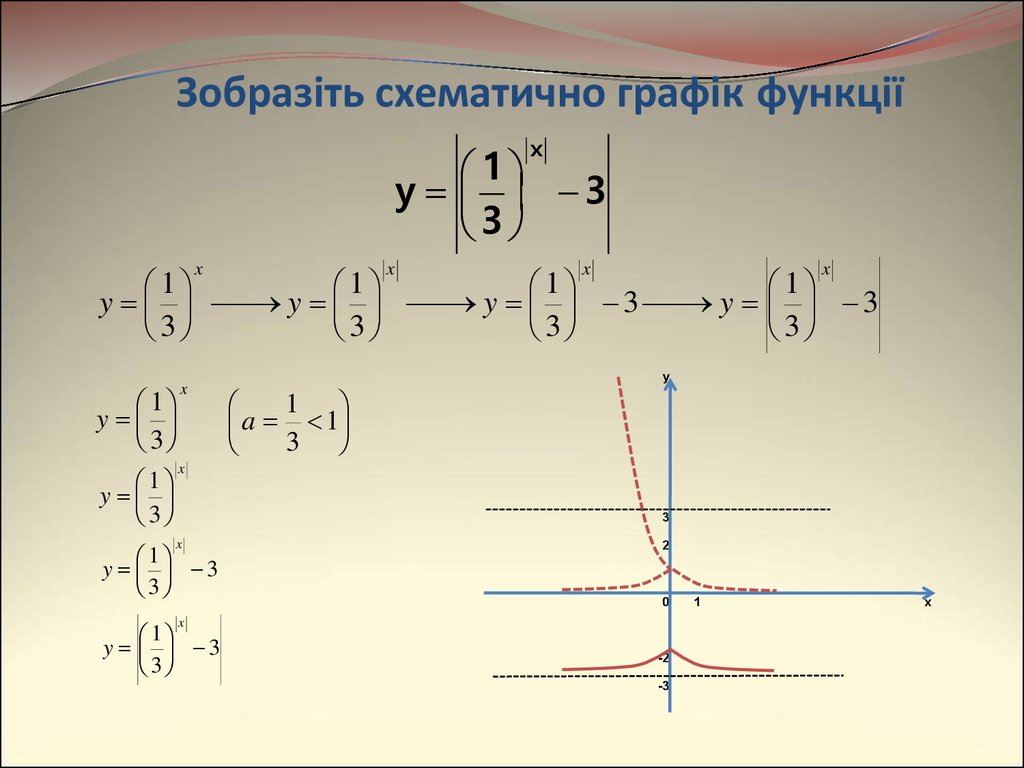
16.
Зобразіть схематично графік функціїx
1
y 3
3
x
x
x
1
1
1
y
y
y 3
y
3
3
3
1
y
3
x
1
y
3
x
x
1
3
3
y
1
a 1
3
3
x
1
y 3
3
2
0
x
1
y 3
3
-2
-3
1
x
17. Тренувальна вправа № 1
Серед наведених функцій показниковою є:y x
y log 1,3 x
1,3
y (4,8)
x
y (0,3)
y x 1,3
x
18. Тренувальна вправа № 2
Серед наведених функцій вибрати ті, що спадають.y (4,8)
1
y
9
x
y (0,001)
x
x
y ( 1)
x
y ( 3)
4
y
3
x
x
19. Тренувальна вправа № 3
Серед наведених функцій вибрати ті, що зростають.1
y
3
y
3
x
x
y (0,01)
x
3
y
x
1
y
9
x
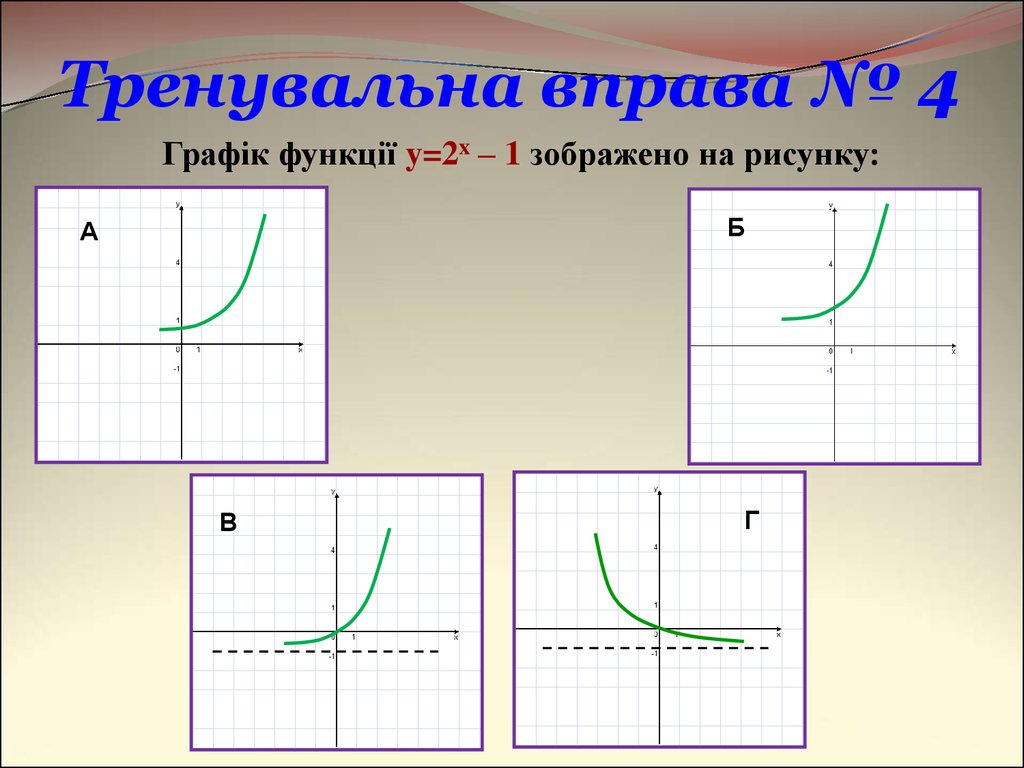
20. Тренувальна вправа № 4
Графік функції y=2x – 1 зображено на рисунку:Б
А
В
Г
21. Тренувальна вправа № 5
Областю значень функції y = 2x + 5 є проміжок:- ;
0;
- ;
5;
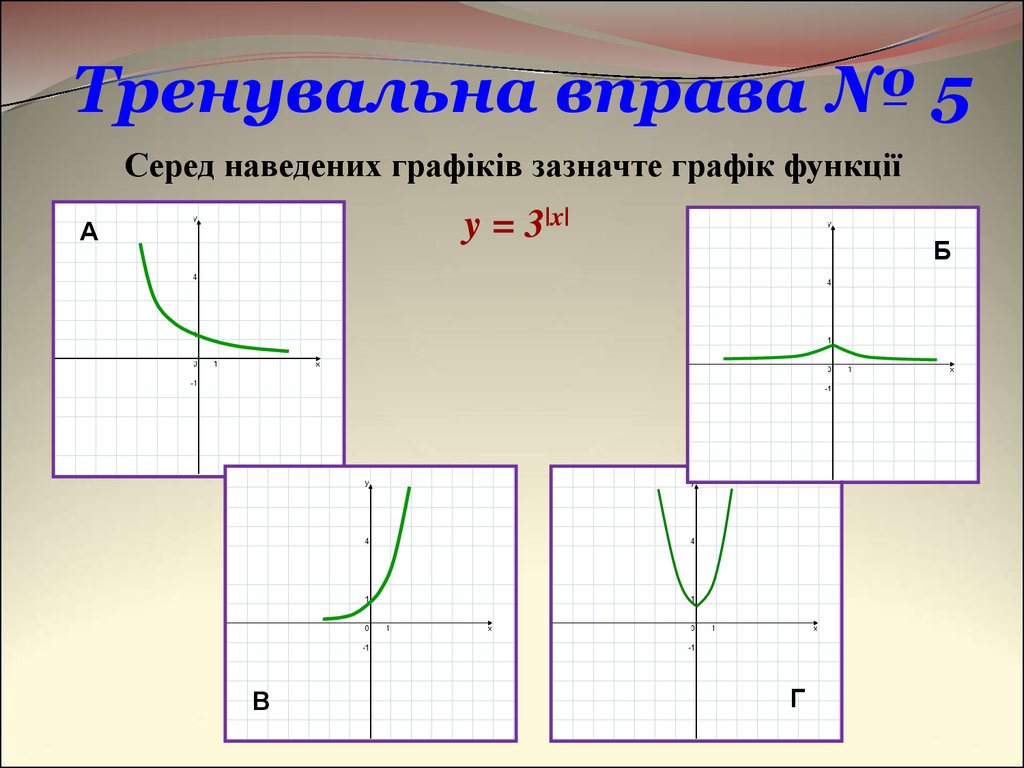
22. Тренувальна вправа № 5
Серед наведених графіків зазначте графік функціїy = 3|x|
А
В
Б
Г











 Математика
Математика








