Расположение прямых в пространстве

1.

D
A
C
B

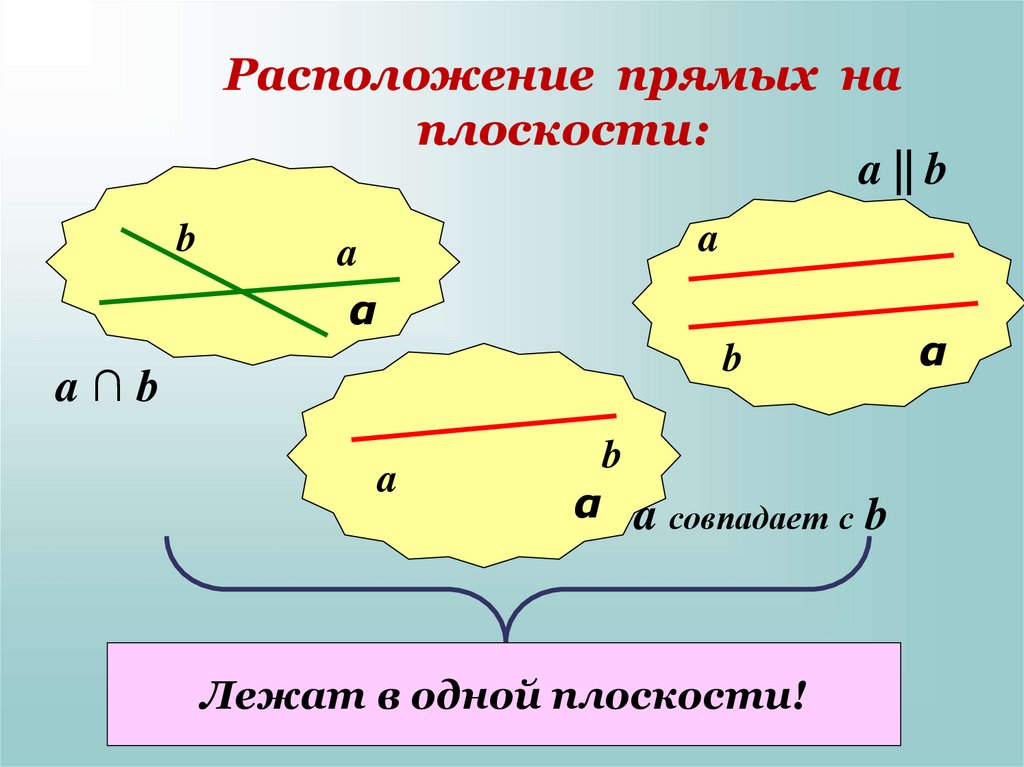
2. Расположение прямых на плоскости:

a || b
b
a
a
α
b
a∩b
a
b
α a совпадает с b
Лежат в одной плоскости!
α

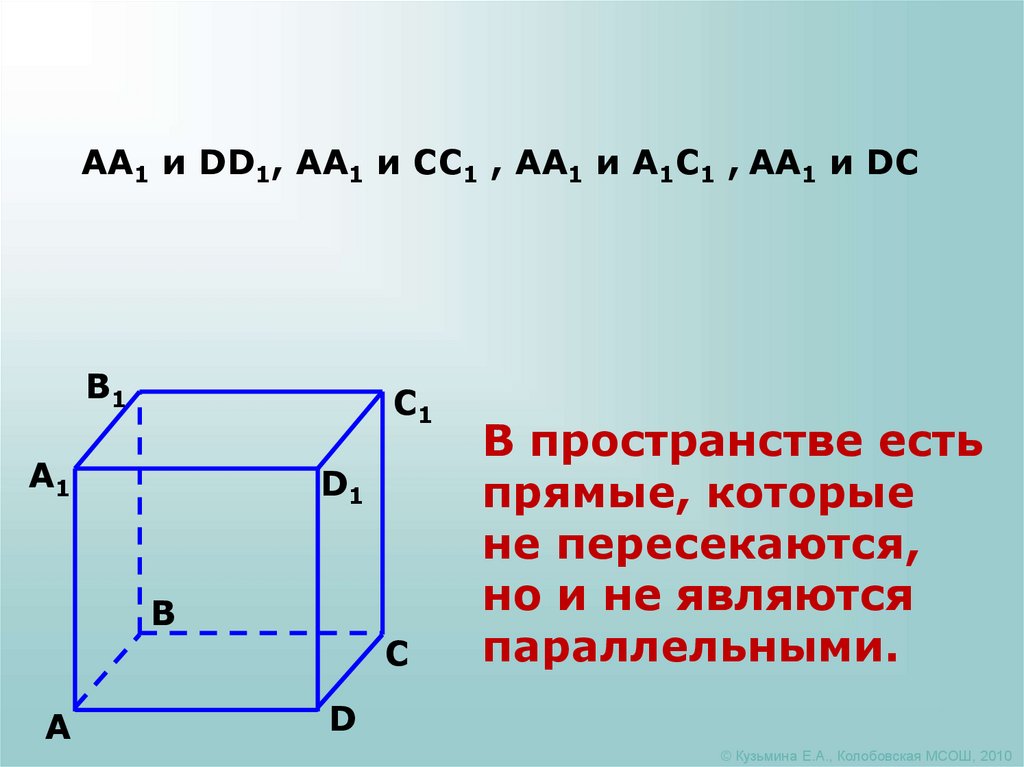
3.

АА1 и DD1, АА1 и СС1 , АА1 и А1С1 , АА1 и DС
B1
C1
A1
D1
B
A
C
В пространстве есть
прямые, которые
не пересекаются,
но и не являются
параллельными.
D
© Кузьмина Е.А., Колобовская МСОШ, 2010

4.

Две прямые называются
скрещивающимися, если они
не лежат в одной плоскости.
c
b
© Кузьмина Е.А., Колобовская МСОШ, 2010

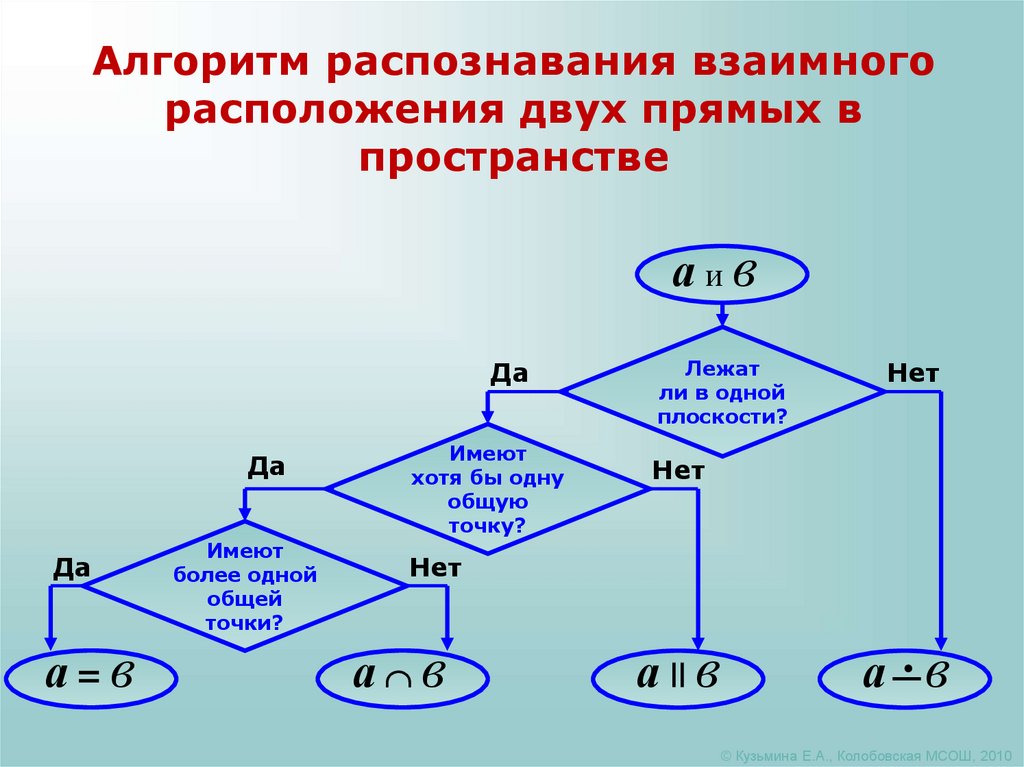
5.

Алгоритм распознавания взаимного
расположения двух прямых в
пространстве
аив
Да
Да
Да
а=в
Имеют
более одной
общей
точки?
Имеют
хотя бы одну
общую
точку?
Лежат
ли в одной
плоскости?
Нет
Нет
Нет
а в
а
в
а .в
© Кузьмина Е.А., Колобовская МСОШ, 2010

6.

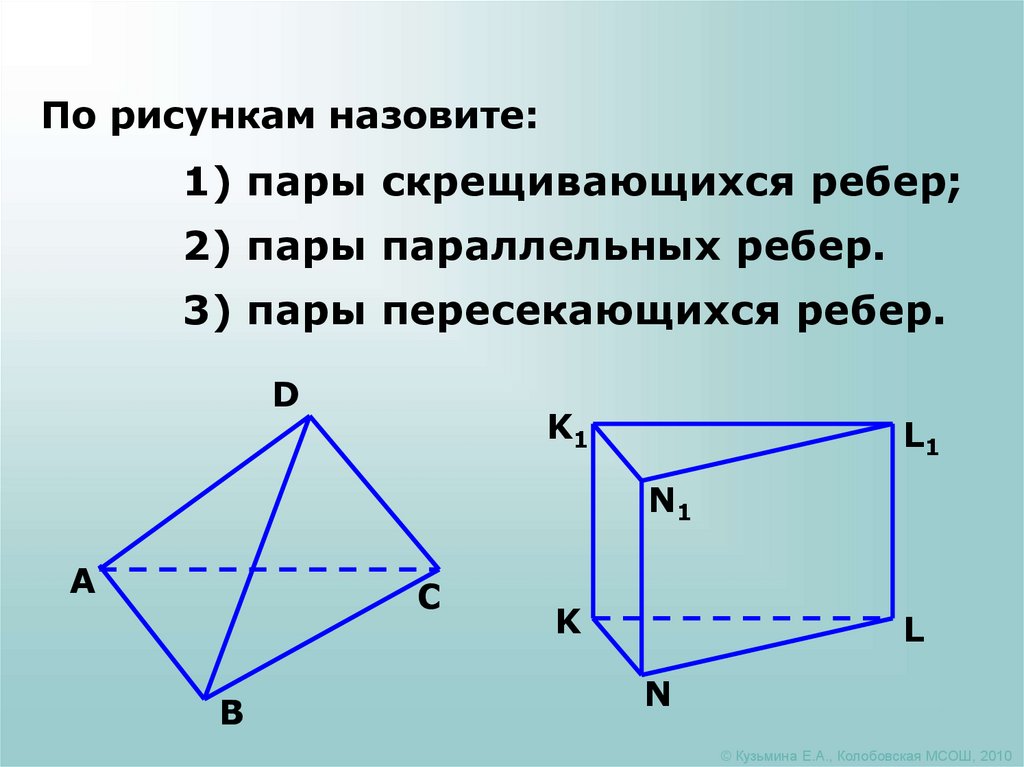
По рисункам назовите:
1) пары скрещивающихся ребер;
2) пары параллельных ребер.
3) пары пересекающихся ребер.
D
K1
L1
N1
A
C
B
K
L
N
© Кузьмина Е.А., Колобовская МСОШ, 2010

7.

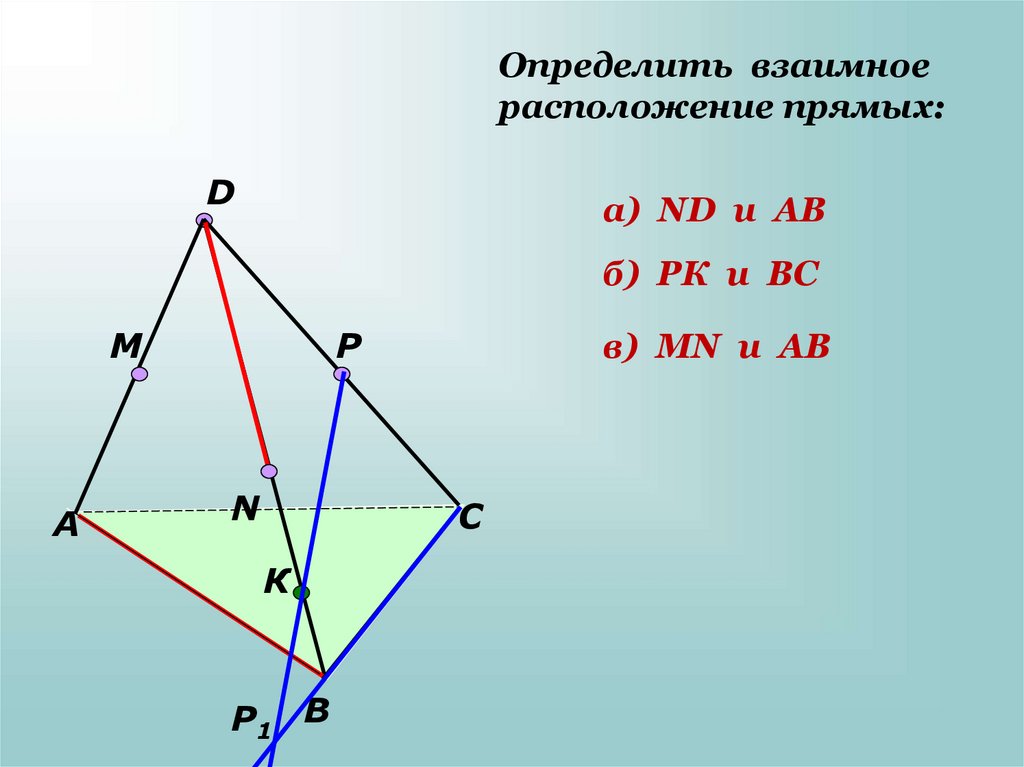
Определить взаимное
расположение прямых:
D
а) ND и AB
б) РК и ВС
M
А
P
N
в) МN и AB
С
К
Р1 В

8.

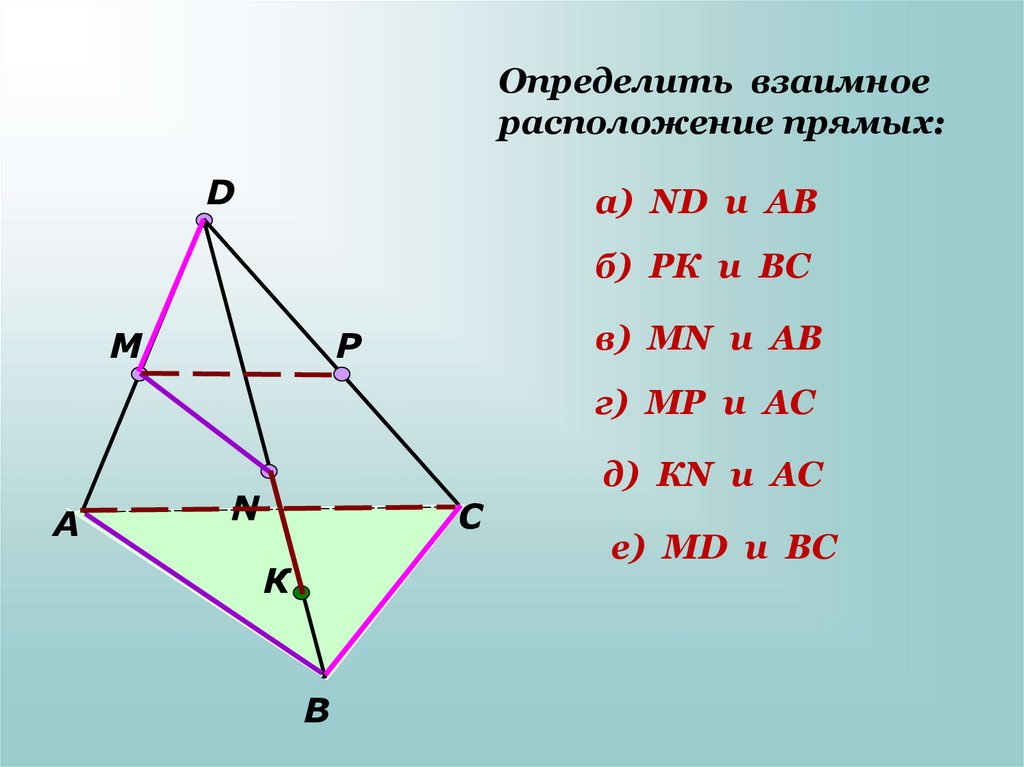
Определить взаимное
расположение прямых:
D
а) ND и AB
б) РК и ВС
M
в) МN и AB
P
г) МР и AС
А
N
С
К
В
д) КN и AС
е) МD и BС

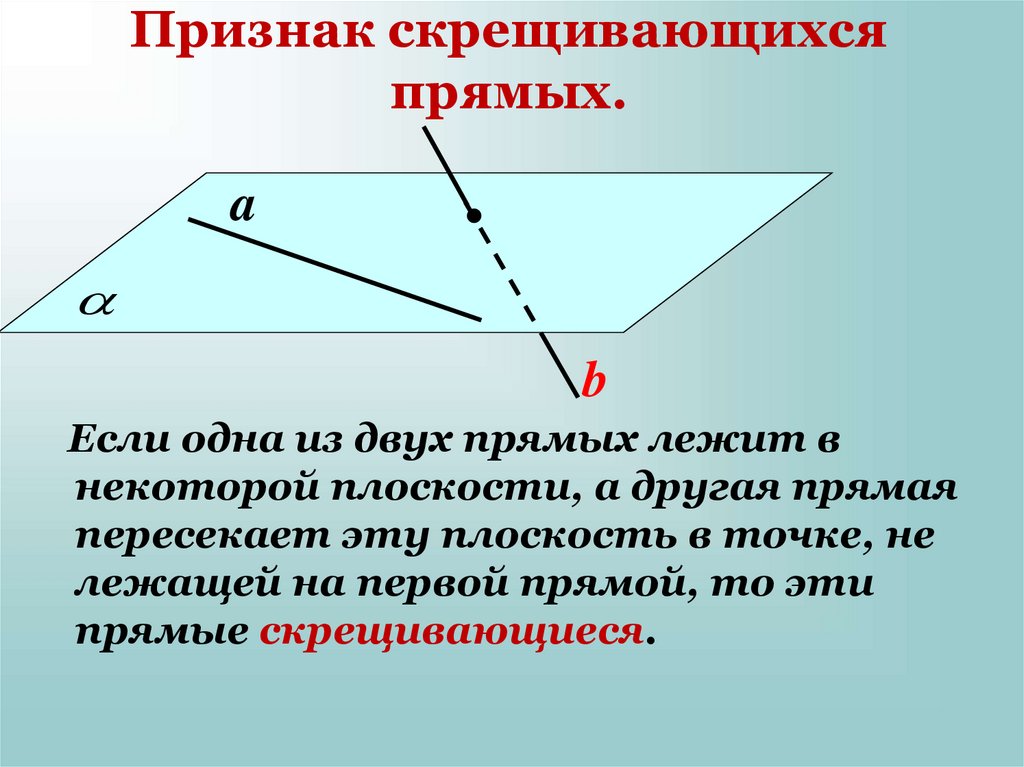
9. Признак скрещивающихся прямых.

a
b
Если одна из двух прямых лежит в
некоторой плоскости, а другая прямая
пересекает эту плоскость в точке, не
лежащей на первой прямой, то эти
прямые скрещивающиеся.

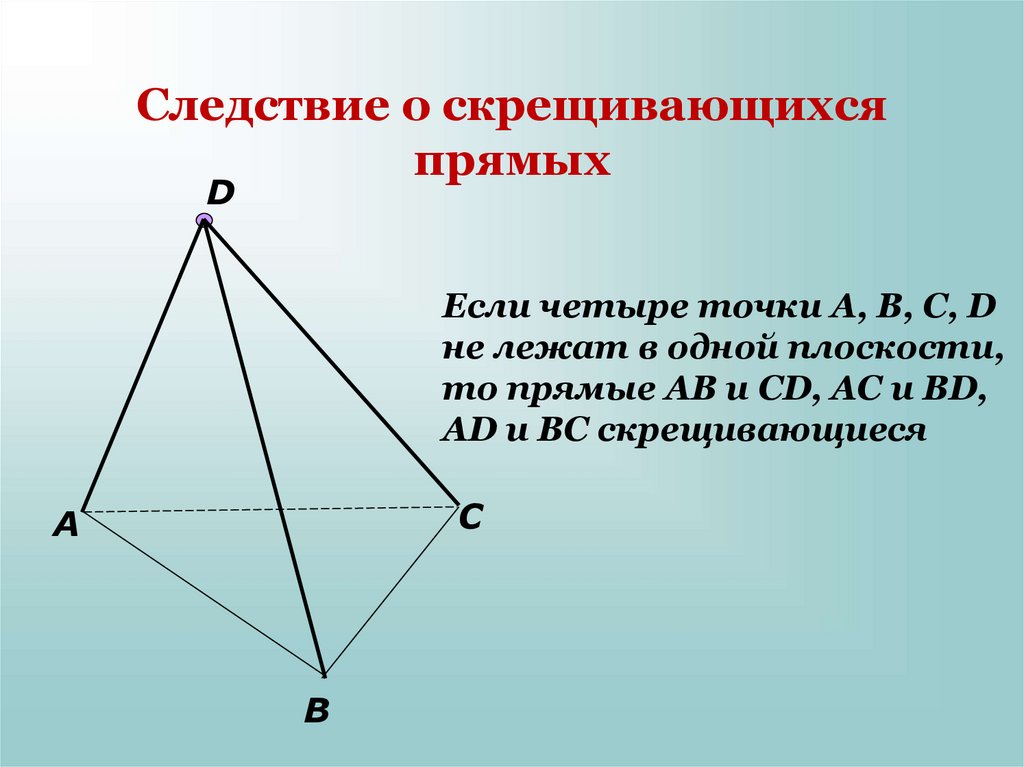
10. Следствие о скрещивающихся прямых

D
Если четыре точки A, B, C, D
не лежат в одной плоскости,
то прямые АВ и СD, AC и BD,
AD и BC скрещивающиеся
С
А
В

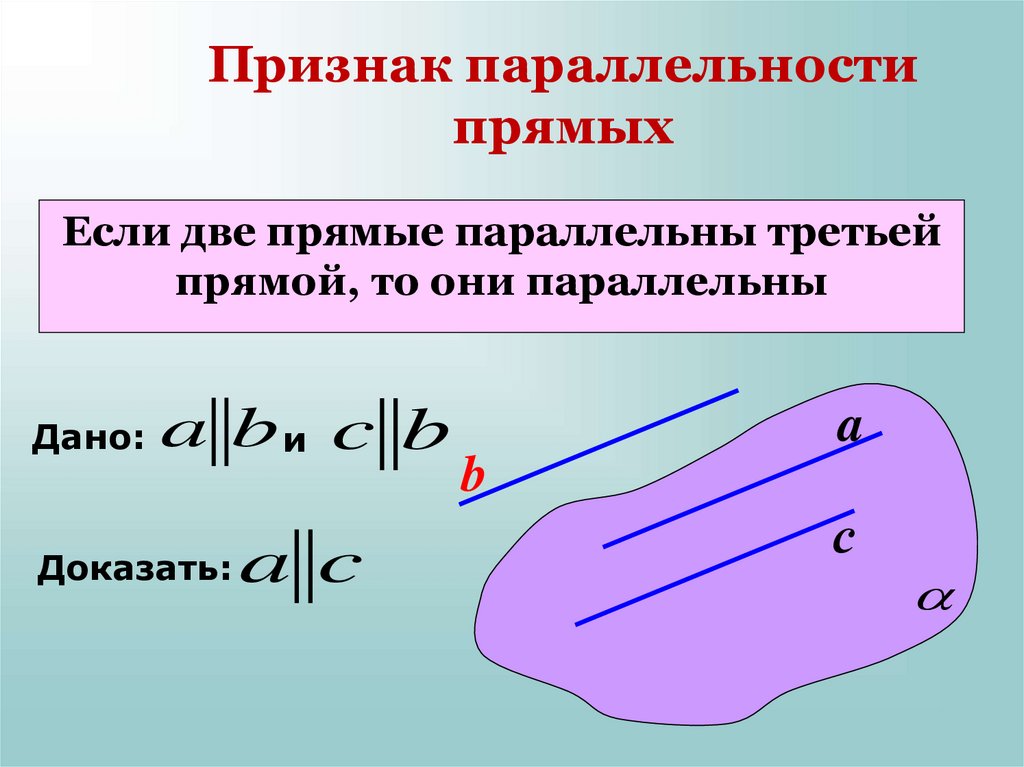
11. Признак параллельности прямых

Если две прямые параллельны третьей
прямой, то они параллельны
Дано:
a bи c b
Доказать:
a c
a
b
с

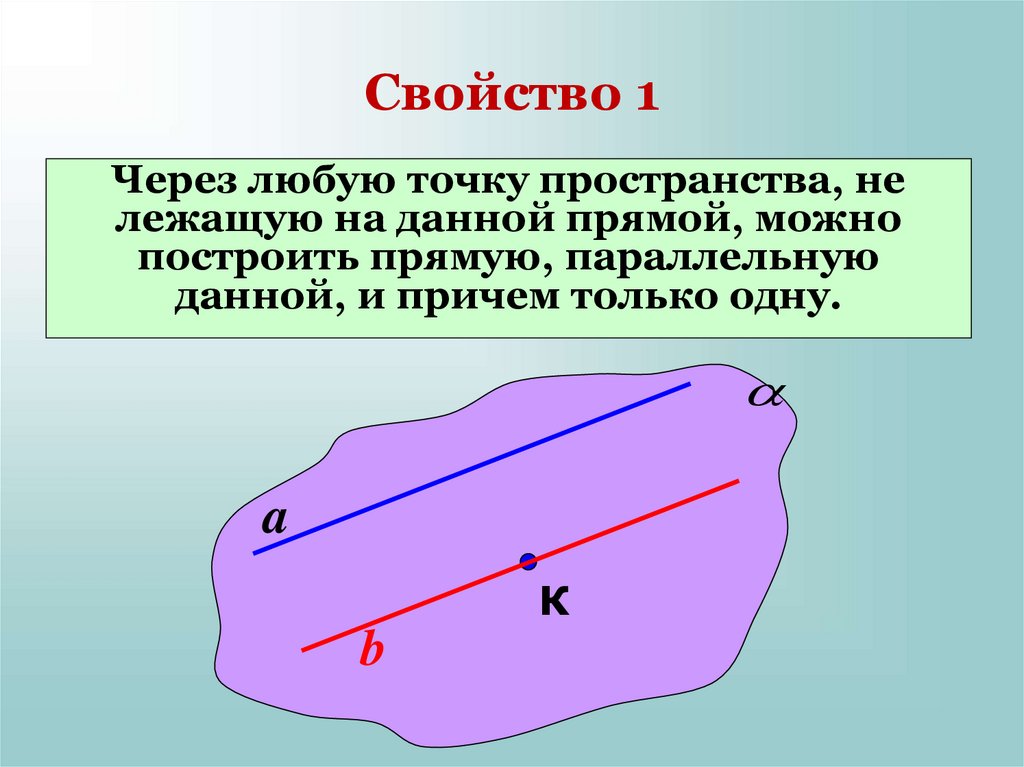
12. Свойство 1

Через любую точку пространства, не
лежащую на данной прямой, можно
построить прямую, параллельную
данной, и причем только одну.
a
К
b

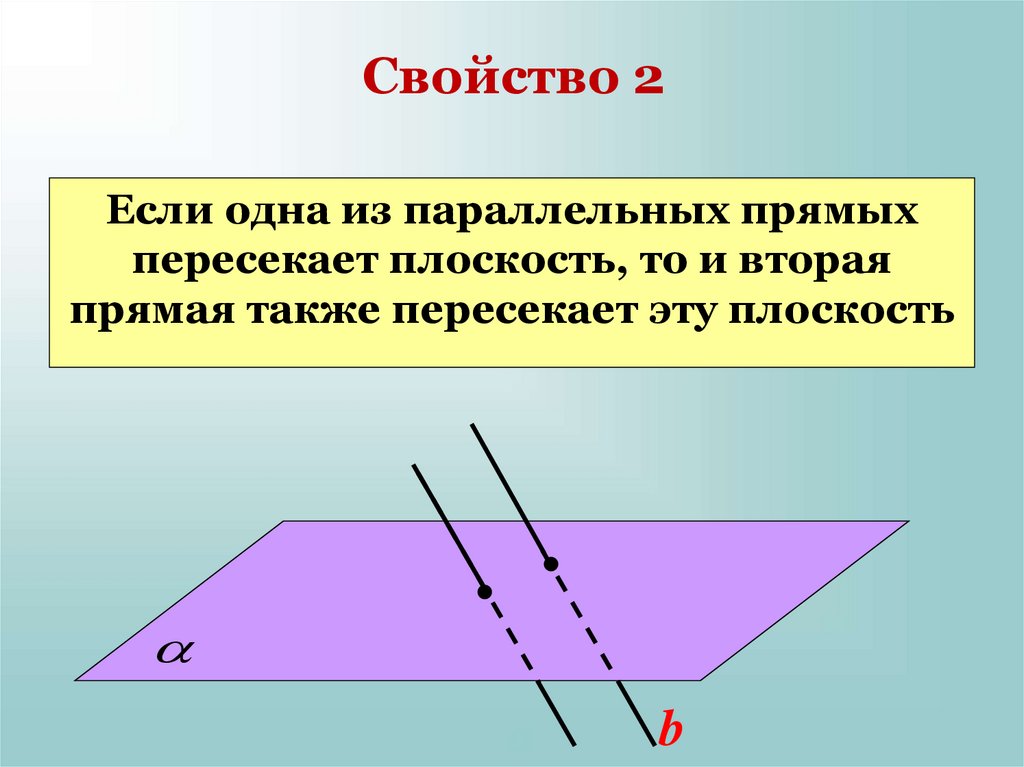
13. Свойство 2

Если одна из параллельных прямых
пересекает плоскость, то и вторая
прямая также пересекает эту плоскость
a
b