Планиметрия. Стереометрия

1. Геометрия

Планиметрия Стереометрия
stereos
телесный, твердый, объемный,
пространственный

2.

Изучить аксиомы стереометрии:
- о взаимном расположении точек,
- о взаимном расположении прямых,
- о взаимном расположении плоскостей
в пространстве.
Изучить некоторые следствия из
аксиом стереометрии.
Показать применение аксиом к
решению задач.
22.12.2021
www.konspekturoka.ru

3.

Раздел геометрии, в котором изучаются
свойства фигур в пространстве, называется
СТЕРЕОМЕТРИЕЙ
Основные фигуры в пространстве:
Точка
Прямая
Плоскость
А
а

4.

A, B, C, …
a, b, c, …
или
AВ, BС, CD, …
, , ,

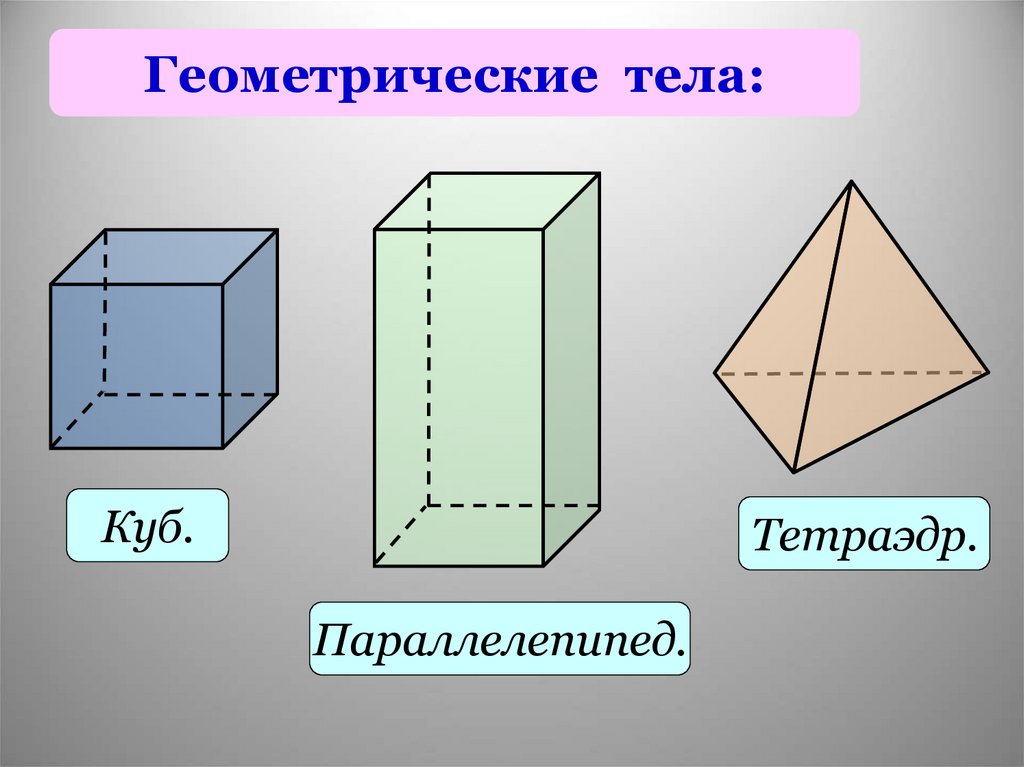
5. Геометрические тела:

Куб.
Тетраэдр.
Параллелепипед.

6. Аксиома

(от греч. axíõma – принятие положения)
Исходное положение
научной теории,
принимаемое без
доказательства

7.

Аксиома 1(С1):
Через три различные
точки, не лежащие
на одной прямой,
можно провести
плоскость и притом
только одну.
α
Α
в
Аϵα, Вϵα, Сϵα

8.

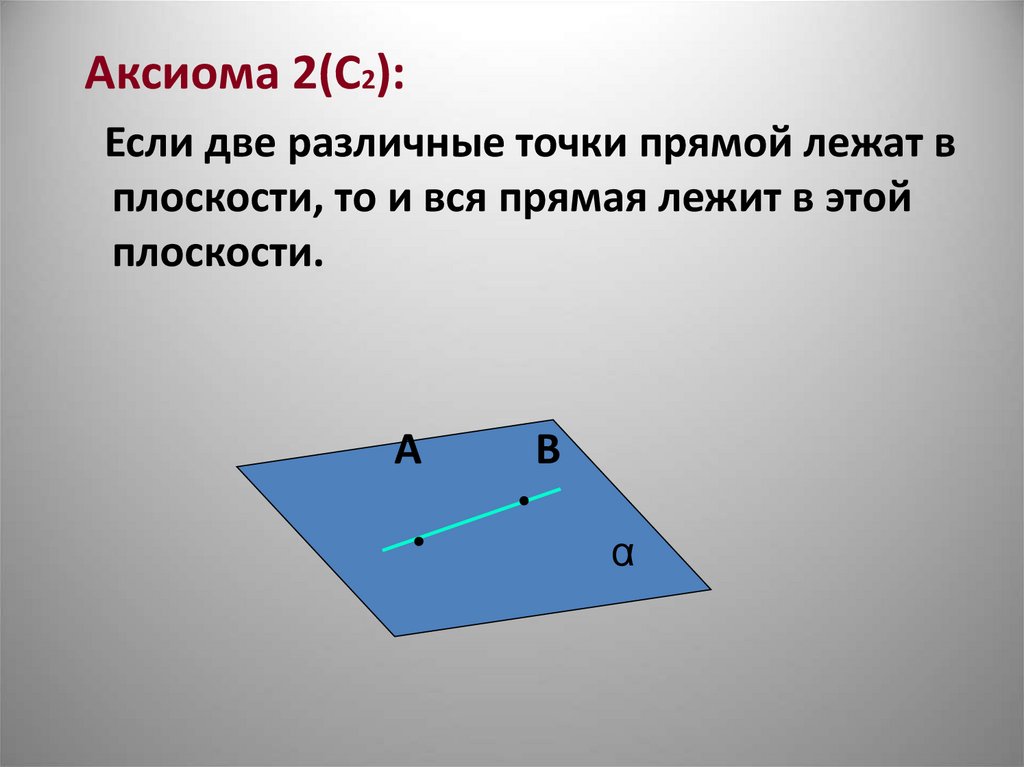
Аксиома 2(С2):
Если две различные точки прямой лежат в
плоскости, то и вся прямая лежит в этой
плоскости.
А
В
α

9.

А
m
α
β
А β
}
α β=m
U
А α
Э
Э
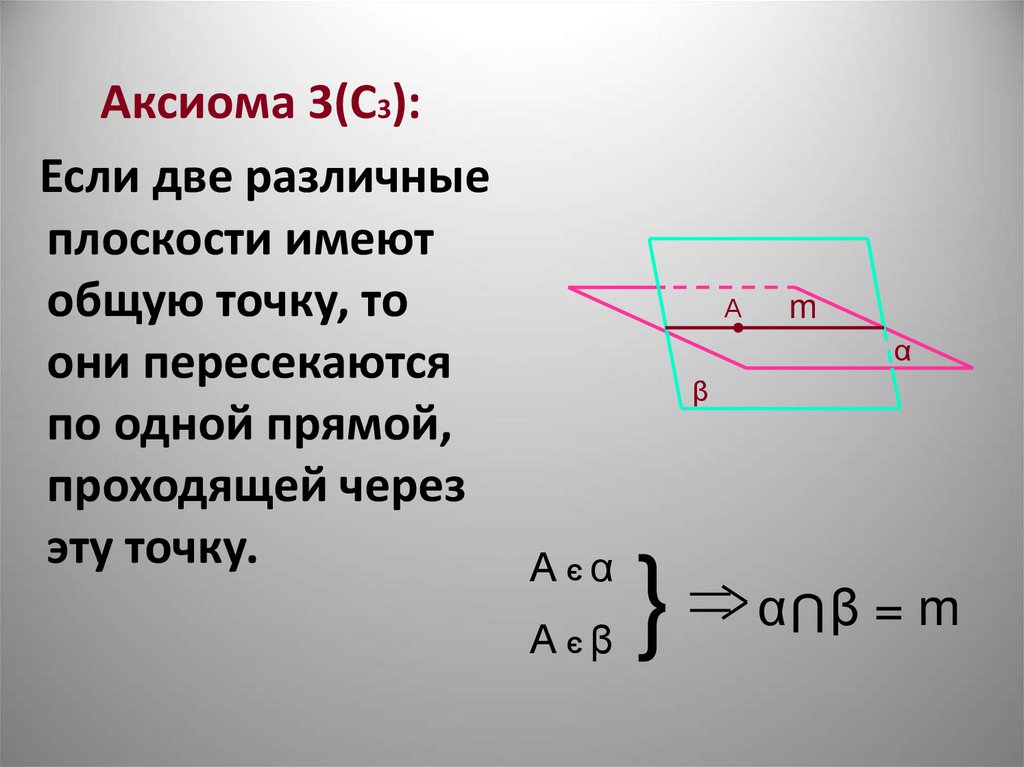
Аксиома 3(С3):
Если две различные
плоскости имеют
общую точку, то
они пересекаются
по одной прямой,
проходящей через
эту точку.

10.

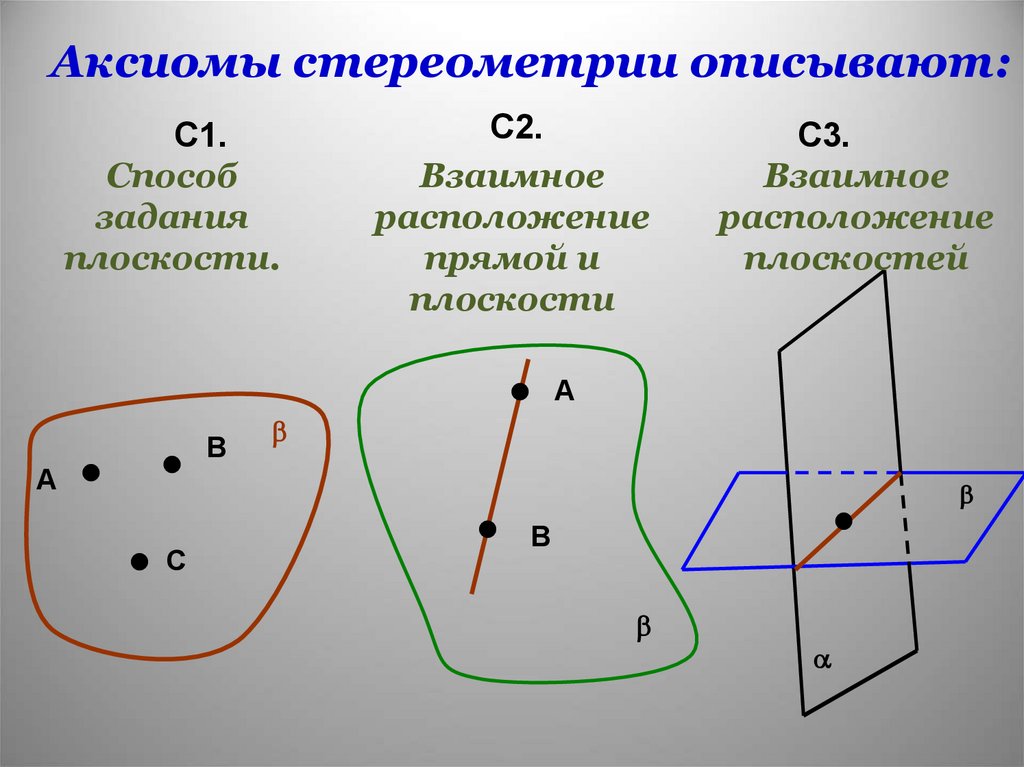
Аксиомы стереометрии описывают:
С1.
Способ
задания
плоскости.
С2.
Взаимное
расположение
прямой и
плоскости
С3.
Взаимное
расположение
плоскостей
А
В
А
С
В

11. АКСИОМЫ СТЕРЕОМЕТРИИ ВОКРУГ НАС

Аксиома1
Через любые три точки , не лежащие на одной прямой, проходит плоскость,
и притом только одна.
Аксиома2
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
Аксиома3
Если две плоскости имеют общую точку, то они имеют прямую,
на которой лежат все общие точки этих плоскостей.

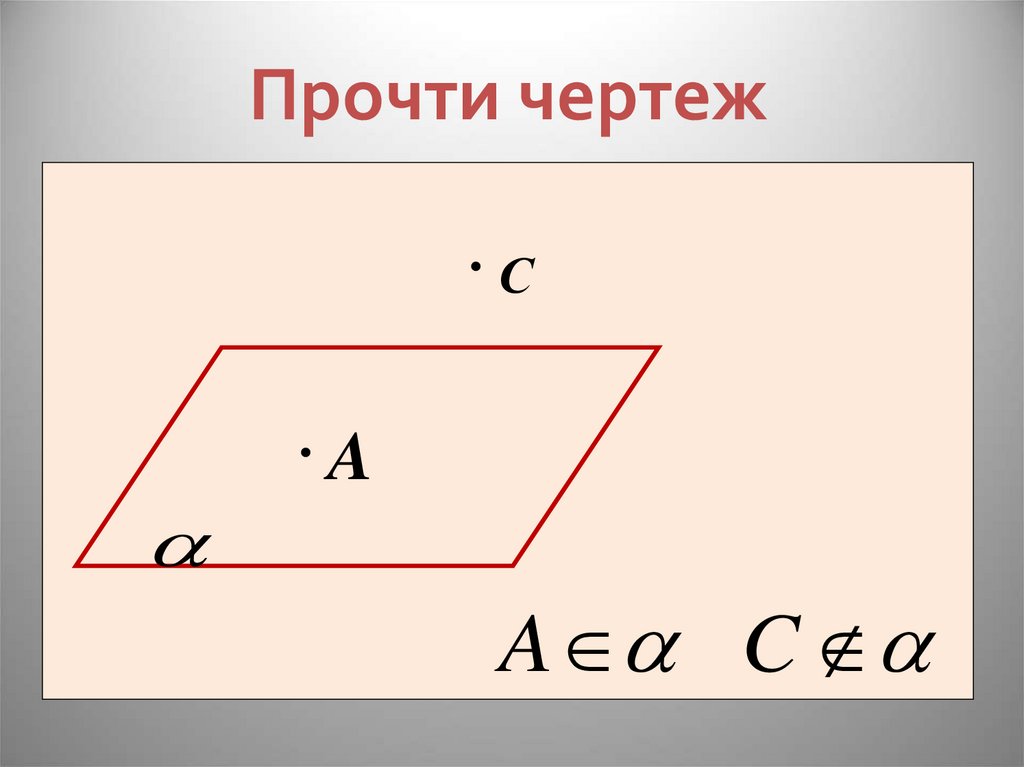
12. Прочти чертеж

С
A
A C

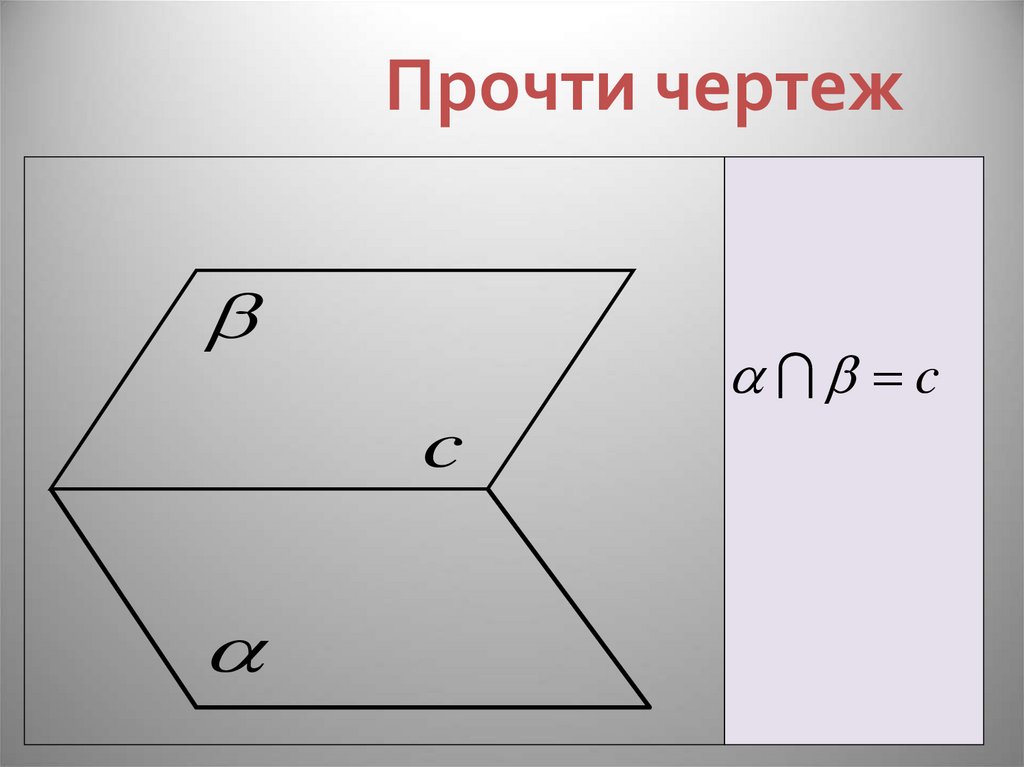
13. Прочти чертеж

b
c
a
b B
B
a
c

14. Прочти чертеж

c
c

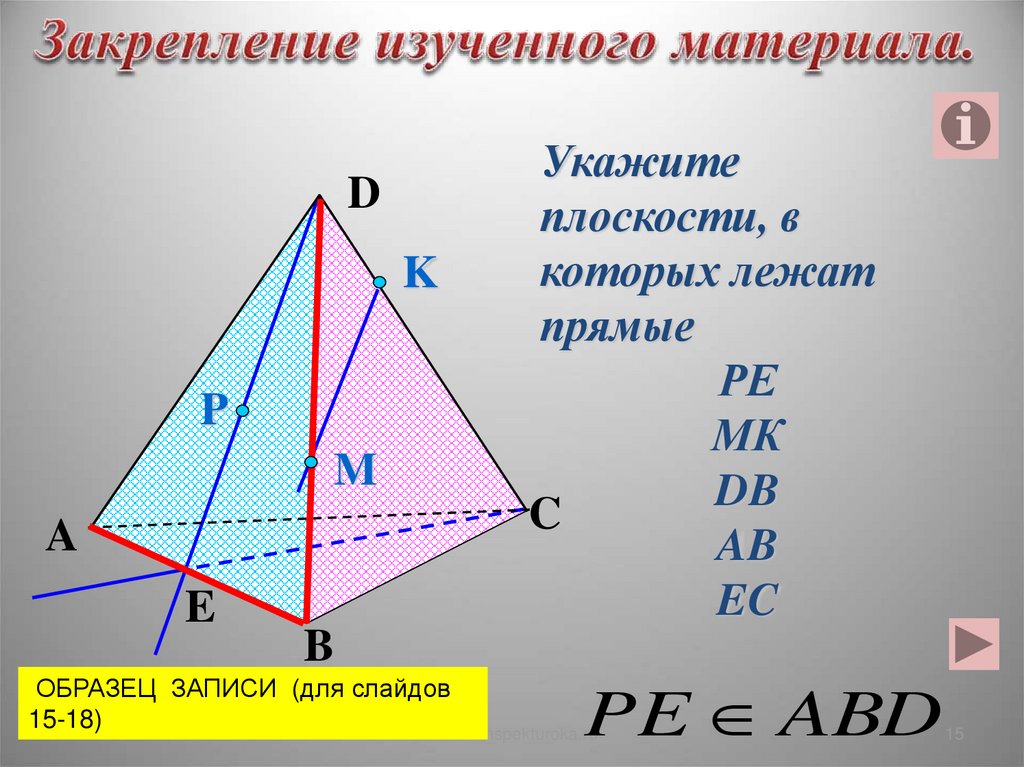
15.

D
K
P
M
A
E
B
Укажите
плоскости, в
которых лежат
прямые
РЕ
МК
DB
C
AB
EC
PE ABD
ОБРАЗЕЦ ЗАПИСИ (для слайдов
15-18)
22.12.2021
www.konspekturoka.ru
15

16.

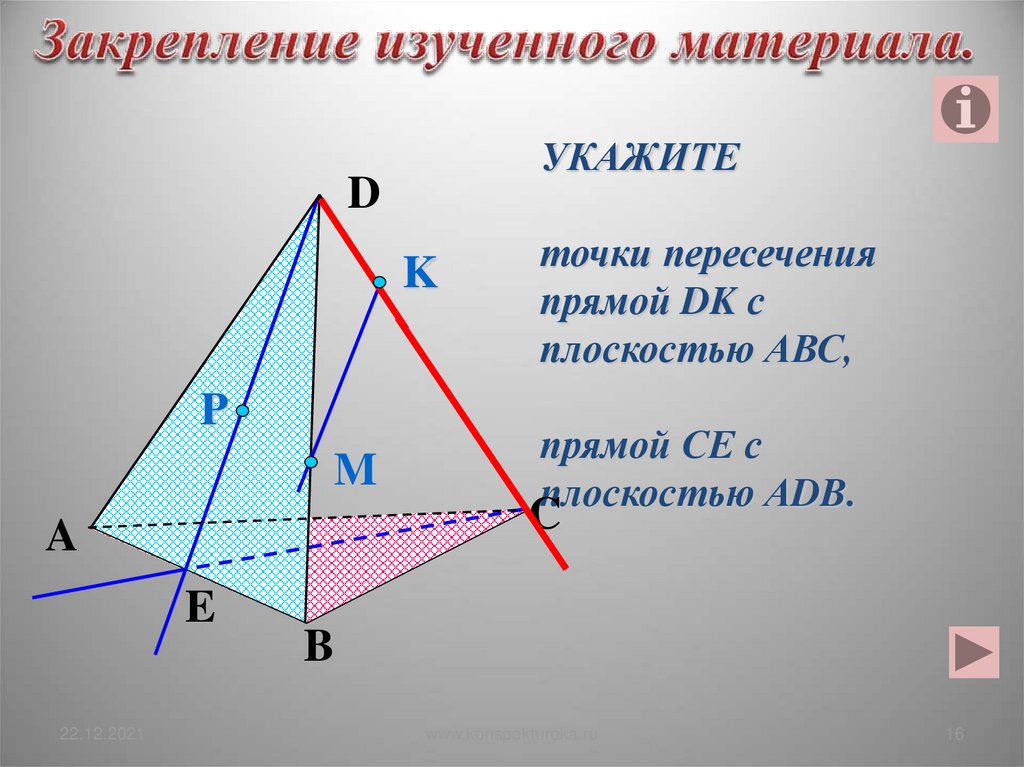
УКАЖИТЕ
D
K
P
M
прямой СЕ с
плоскостью АDB.
C
A
E
22.12.2021
точки пересечения
прямой DK с
плоскостью АВС,
B
www.konspekturoka.ru
16

17.

D
K
Назовите точки,
лежащие в
плоскостях АDB и
DBC
P
M
C
A
E
22.12.2021
B
www.konspekturoka.ru
17

18.

D
K
P
M
A
E
22.12.2021
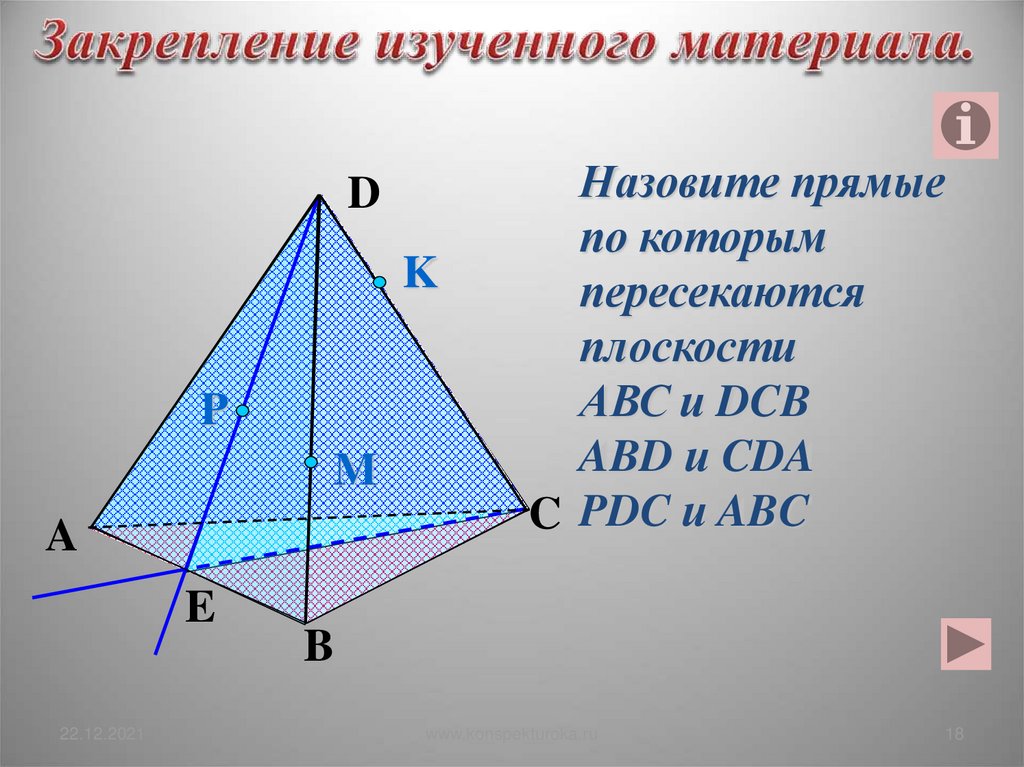
Назовите прямые
по которым
пересекаются
плоскости
АВС и DCB
ABD и CDA
C PDC и ABC
B
www.konspekturoka.ru
18

19. Следствия из аксиом

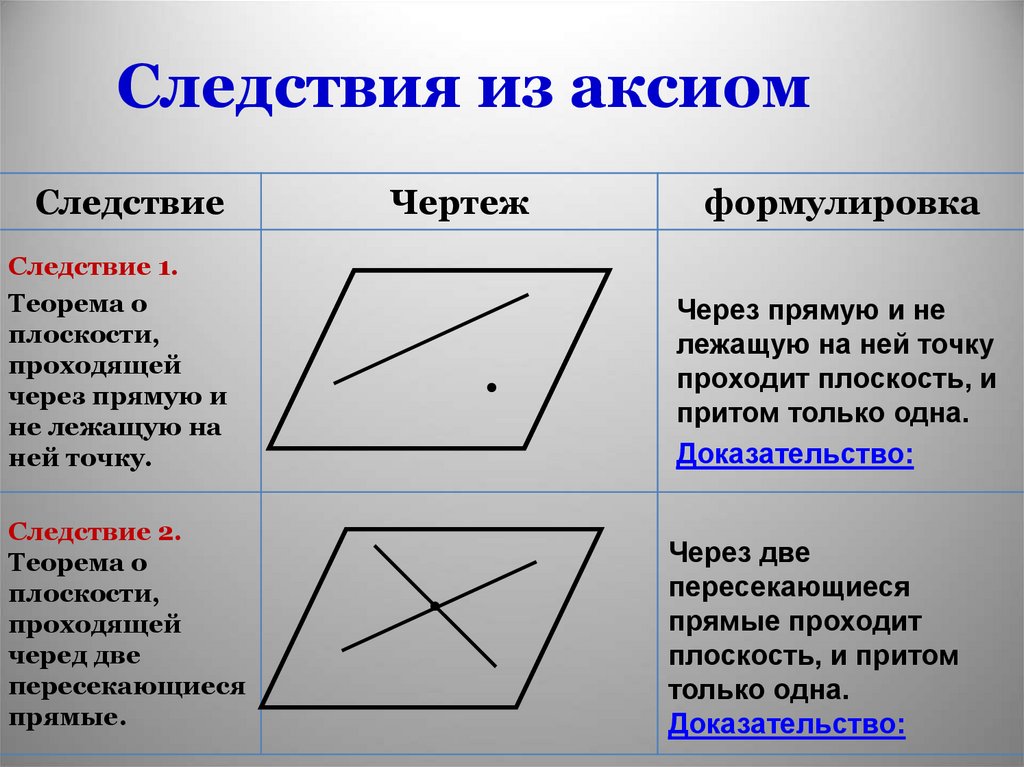
Следствие
Следствие 1.
Теорема о
плоскости,
проходящей
через прямую и
не лежащую на
ней точку.
Следствие 2.
Теорема о
плоскости,
проходящей
черед две
пересекающиеся
прямые.
Чертеж
формулировка
Через прямую и не
лежащую на ней точку
проходит плоскость, и
притом только одна.
Доказательство:
Через две
пересекающиеся
прямые проходит
плоскость, и притом
только одна.
Доказательство:

20. Следствия из аксиом

Работа с учебником (стр6-7)
ТЕОРЕМА 1 Через прямую и не лежащую на ней точку
проходит плоскость, и притом только одна.
Выполнить чертеж
Записать : Доказательство
ТЕРЕМА 2 Через две пресекающиеся прямые проходит
плоскость, и притом только одна.
Выполнить чертеж
Записать : Доказательство

21.

Самостоятельная работа
1 вариант.
2 вариант
1. Назовите основные фигуры
на плоскости.
1. Назовите основные фигуры
в пространстве.
2. Сформулируйте аксиому А2
2. Сформулируйте аксиому А1
3. Могут ли прямая и
плоскость иметь две общие
точки?
3. Сколько плоскостей можно
провести через прямую и не
лежащую на ней точку?
4. Сколько плоскостей можно
провести через три точки?
4. Сформулируйте аксиому А3
5. Сколько может быть общих
точек у прямой и плоскости?
5. Могут ли прямая и
плоскость иметь одну общую
точку?