Похожие презентации:
Пирамида
1.
2. Пирамидой называется многогранник, который состоит из плоского многоугольника, – основания пирамиды, точки, не лежащей в
плоскостиоснования, – вершины пирамиды и всех отрезков, соединяющих вершину
пирамиды с точками.
S
вершина
боковые ребра
боковые грани
D
E
А
основание
C
B
3.
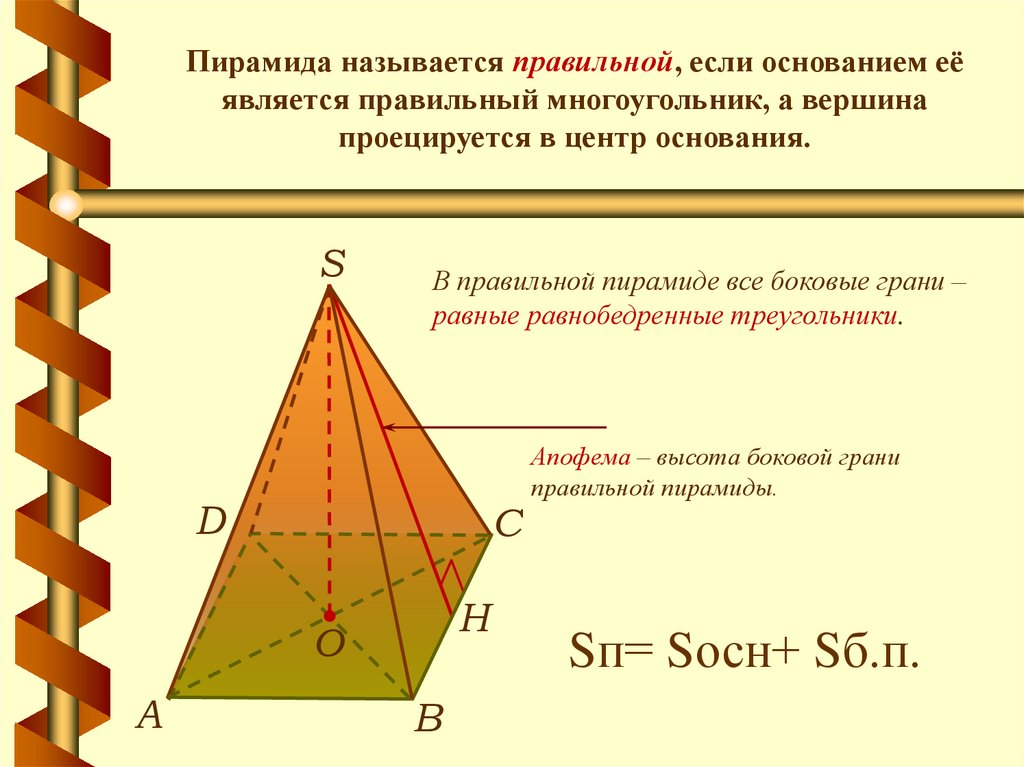
Пирамида называется правильной, если основанием еёявляется правильный многоугольник, а вершина
проецируется в центр основания.
S
В правильной пирамиде все боковые грани –
равные равнобедренные треугольники.
D
С
Н
О
А
В
Апофема – высота боковой грани
правильной пирамиды.
Sп= Sосн+ Sб.п.
4.
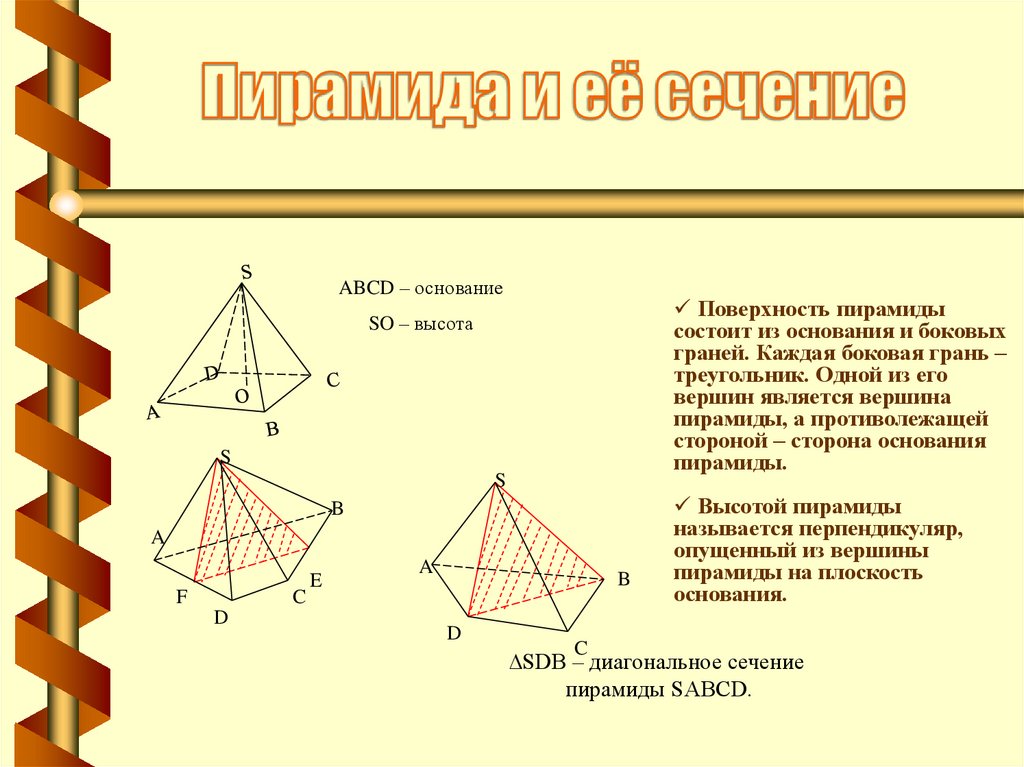
ABCD – основаниеПоверхность пирамиды
состоит из основания и боковых
граней. Каждая боковая грань –
треугольник. Одной из его
вершин является вершина
пирамиды, а противолежащей
стороной – сторона основания
пирамиды.
SO – высота
S
S
B
A
F
C
D
E
A
B
D
C
Высотой пирамиды
называется перпендикуляр,
опущенный из вершины
пирамиды на плоскость
основания.
∆SDB – диагональное сечение
пирамиды SABCD.
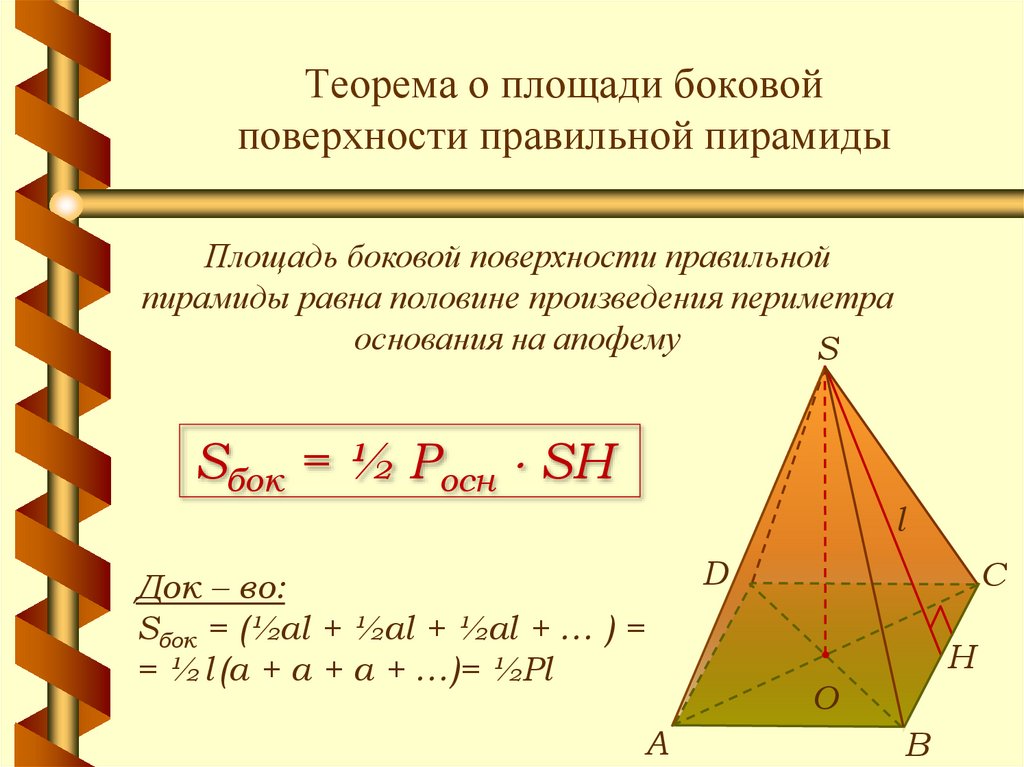
5. Теорема о площади боковой поверхности правильной пирамиды
Площадь боковой поверхности правильнойпирамиды равна половине произведения периметра
основания на апофему
S
Sбок = ½ Pосн SH
l
Док – во:
Sбок = (½al + ½al + ½al + … ) =
= ½ l (a + a + a + …)= ½Pl
А
D
С
Н
О
В
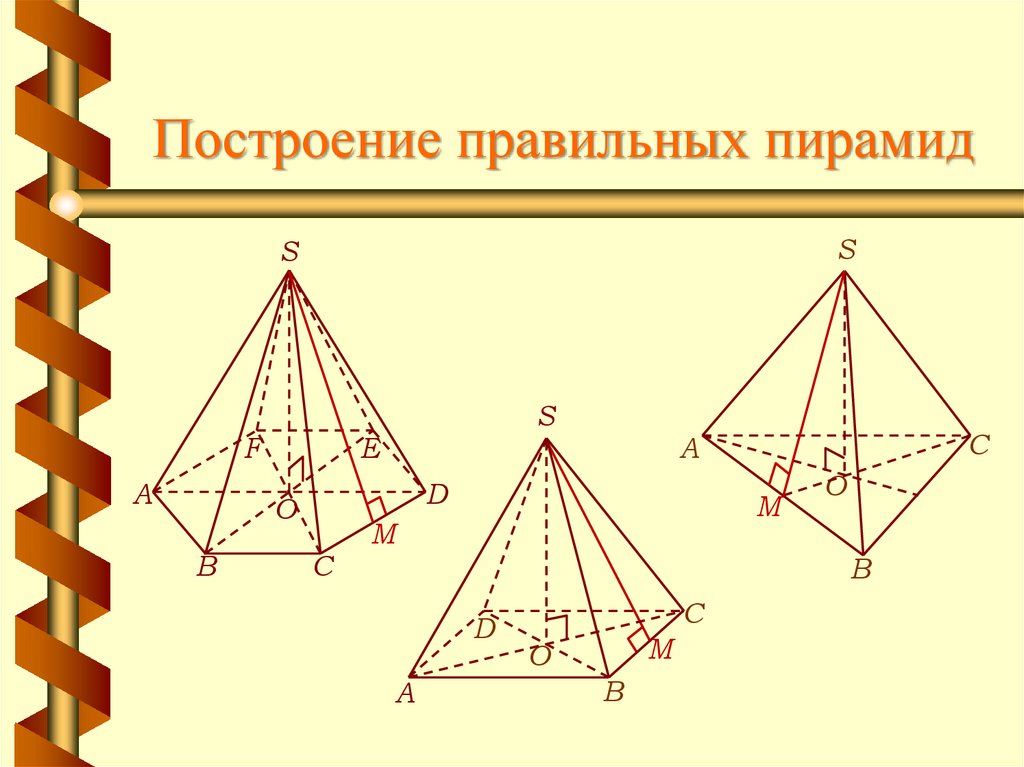
6. Построение правильных пирамид
SS
F
A
E
C
С
А
D
O
B
S
M
M
O
В
D
А
C
M
O
В
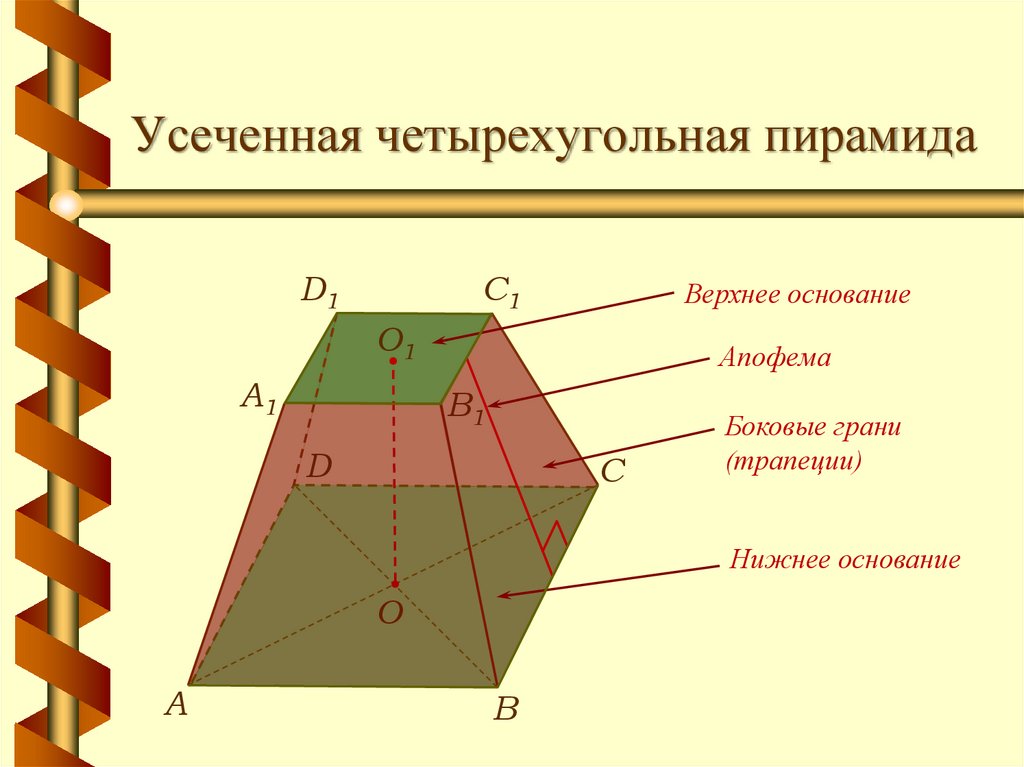
7. Усеченная четырехугольная пирамида
D1C1
Верхнее основание
О1
A1
Апофема
B1
D
С
Боковые грани
(трапеции)
Нижнее основание
О
А
В
8. Площадь боковой поверхности правильной усеченной пирамиды
Площадь боковой поверхности правильной усеченнойпирамиды равна произведению полусуммы периметров
оснований на апофему.
D
A
D1
C
О
B
a
Sбок=½(P1осн.+ P2осн.) l
l
О1
А1
b
В1
С1
Док – во:
Sбок = (½(a+b)l + ½(a+b)l +
+½(a+b)l + … ) =
= ½ l ((a+a+…)+(b+b+…))=
=½(P1осн.+ P2осн.) l



 Математика
Математика








