Технология подготовки учащихся к овладению геометрическими методами решения задач с параметрами. Занятие №4

1. Занятие №4. Технология подготовки учащихся к овладению геометрическими методами решения задач с параметрами.

Прокофьев Александр Александрович,
Зав.каф. ВМ-1, НИУ МИЭТ

2. Содержание курса

№
Тема занятий
1
Основные структурные изменения и особенности проведения
государственной аттестации учащихся в 2015. Технология
подготовки учащихся к овладению алгебраическими методами
решения задач с параметрами.
2
Технология подготовки учащихся к овладению функциональными
методами решения задач с параметрами.
3
Технология подготовки учащихся к овладению функциональнографическими методами решения задач с параметрами.
4
Технология подготовки учащихся к овладению геометрическими
методами решения задач с параметрами.
5
Технология подготовки учащихся к овладению решения задач с
параметрами комбинированными методами.
Итоговая аттестация
По результатам посещаемости и успешности выполнения
контрольных работ.
2

3. Содержание занятия

• О геометрических методах решения задач с параметрами
• Геометрический метод в задачах с параметром в литературе
для подготовки к ЕГЭ 2015 (проф. уровень)
• Язык формул и расстояний
• Соответствие формул и геометрических образов
• Технология подготовки учащихся к овладению
геометрическими методами решения задач с параметрами
(знакомство с основными типами задач)
• Параметры в геометрических задачах
• Печатные и электронные ресурсы.
3

4. О геометрическом методе решения задач с параметром

Задачи, решаемые
этим методом, содержат
«геометрический подтекст», поскольку их составление
изначально и решение в последующем подразумевает
использование различных геометрических соображений.
Метод основан на том, что между геометрическими и
алгебраическими задачами, между языком алгебры
(«языком формул») и языком геометрии («языком
расстояний») существует неоспоримая связь, известная
со времен Декарта.
4

5. О геометрических методах решения задач с параметрами

Можно выделить два вида задач с параметрами, при решении которых
используются геометрические методы:
1) задачи с параметром, использующие в решении геометрические идеи;
2) непосредственно геометрические задачи, при решении которых
применяется метод введения параметра.
В первом случае графические интерпретации основываются еще и на
геометрических представлениях, а решение – на использовании формул
расстояния (между двумя точками; от точки до прямой на плоскости или до
плоскости в пространстве), уравнений (прямой, пары параллельных или
пересекающихся прямых; окружности; отрезка или параллелограмма), то есть
основывается на использовании метода координат и геометрических формул.
Само доказательство или решение задачи в этом случае опирается на
наглядные представления, а геометрические идеи являются основанием для
решения ряда алгебраических задач: уравнений, неравенств, вычисления
наибольшего и наименьшего значений некоторых выражений.
Во втором случае решение геометрической задачи сводится к решению
уравнения или системы уравнений и требует умения применять
соответствующий алгебраический инструментарий.
5

6. Геометрический метод в задачах с параметром в литературе для подготовки к ЕГЭ 2015 (проф. уровень)

6

7. Геометрический метод в задачах с параметром в литературе для подготовки к ЕГЭ 2015 (проф. уровень)

7

8. Функционально-графические методы в электронных пособиях Прокофьева А.А. и Корянова А.Г.

Из оглавления пособия 2011 года:
Адреса:
http://alexlarin.net/ege/2012/C52012. html
и
http://www.alexlarin.net/ege/2011/c
52011.html
Из оглавления пособия 2012 года:
8

9. Язык формул и расстояний

«Алгебра – не что иное, как записанная в символах геометрия,
а геометрия – это просто алгебра, воплощенная в фигурах»
– София Жермен (1776-1831), французский математик
«Арифметические знаки – это записанные геометрические фигуры,
а геометрические фигуры – это нарисованные формулы»
– Давид Гильберт (1862-1943), немецкий математик
«Но когда эти науки (алгебра и геометрия) объединились, они
энергично поддержали друг друга и быстро зашагали к совершенству»
– Жозе́ф Луи́ Лагра́нж (1736-1813), французский математик
Таблица соответствия между языками
алгебры («язык формул») и геометрии («язык расстояний»)
9

10. Формула расстояния между двумя точками

10

11. Применение формулы расстояния между двумя точками на координатной оси

11

12. Язык расстояний на языке формул.-----------------

12

13. Язык расстояний на языке формул.-----------------

13

14. Язык формул на языке расстояний

14

15. Язык формул на языке расстояний

15

16. Язык формул на языке расстояний.

16

17. Соответствие формул и геометрических образов

Рассмотрим соответствие некоторых уравнений, неравенств и просто
выражений и их геометрических образов на координатной плоскости Oxy
(таблица 1), и их использование при решении задач.
17

18. Уравнение прямой

1
2
Учебник. Шабунин М.И., Прокофьев А.А. Математика. Алгебра. Начала
математического анализа. Проф. Уровень: учебник для 11 класса. − М.:
БИНОМ. Лаборатория знаний. 2012. − 391 с.
18

19. Задачи для самостоятельного решения

1
2
19

20. Системы двух линейных уравнений

20

21. Системы двух линейных уравнений

21

22. Система линейных неравенств

22

23. Соответствие формул и геометрических образов

23

24. Соответствие формул и геометрических образов

24

25. Соответствие формул и геометрических образов

25

26. Соответствие формул и геометрических образов

26

27. Соответствие формул и геометрических образов

27

28. Соответствие формул и геометрических образов

28

29. Расположение прямой и окружности

29

30. Пример из вариантов ЕГЭ 2011

30

31. Пример с «пучком прямых» (ЕГЭ 2013)

31

32. Использование уравнения окружности

32

33. Теоремы о взаимном расположении двух окружностей

33

34. Соответствие формул и геометрических образов

34

35. Соответствие формул и геометрических образов

35

36. Соответствие формул и геометрических образов

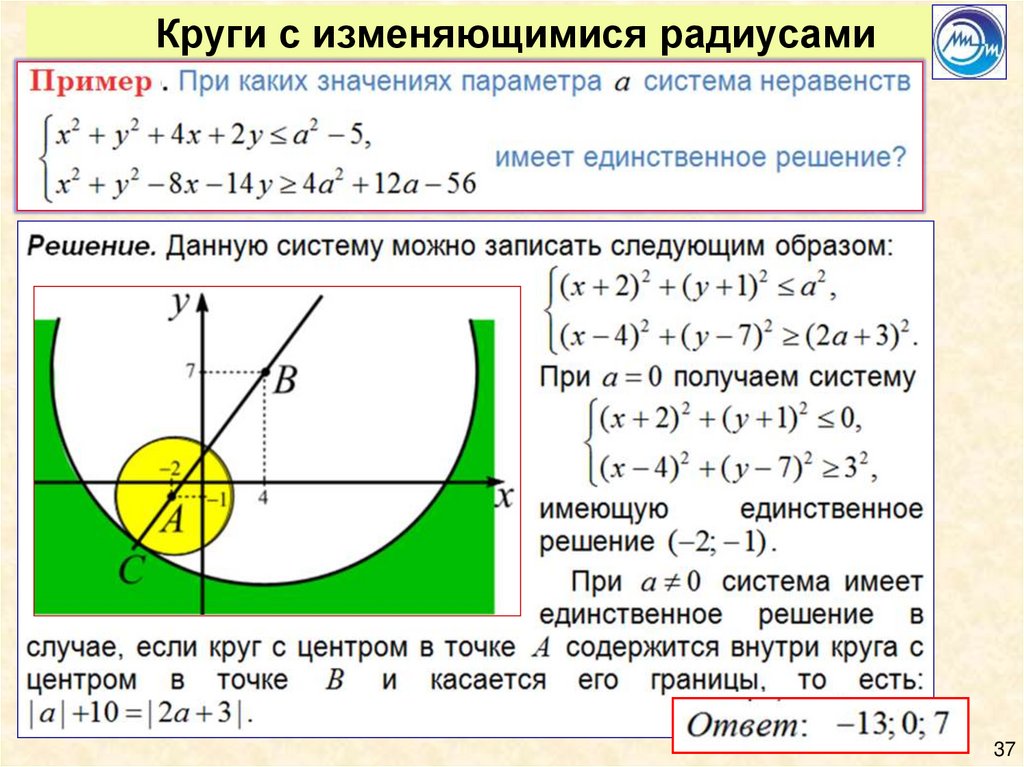
36

37. Круги с изменяющимися радиусами

37

38. Соответствие формул и геометрических образов.

38

39. Соответствие формул и геометрических образов

39

40. Использование уравнения сферы

40

41. Задачи для самостоятельного решения

1
2
3
41

42. Соответствие формул и геометрических образов

42

43. Соответствие формул и геометрических образов

43

44. Соответствие формул и геометрических образов

44

45. Соответствие формул и геометрических образов

45

46. Соответствие формул и геометрических образов

46

47. Соответствие формул и геометрических образов

47

48. Окружность с изменяющимся радиусом

48

49. Задачи для самостоятельного решения

1
2
49

50. Соответствие формул и геометрических образов

50

51. Неравенство треугольника, уравнение отрезка

51

52. Для самостоятельной работы

52

53. Применение уравнения отрезка в радикалах

53

54. Применение уравнения отрезка в радикалах

54

55. Применение уравнения отрезка в радикалах

55

56. Применение уравнения отрезка в радикалах

56

57. Формула расстояния от точки до прямой на плоскости

57

58. Формула расстояния от точки до прямой

58

59. Катится круг

59

60. Формула расстояния от точки до прямой

60

61. Векторные интерпретации в алгебре

61

62. Векторные интерпретации в алгебре ------------

62

63. Векторные интерпретации в алгебре ------------

Векторные интерпретации в алгебре -----------Задача могла быть решена и с использованием формулы
отрезка в радикалах (неравенства треугольника).
63

64. Векторные интерпретации в алгебре ------------

64

65. Векторные интерпретации в алгебре ------------

65

66. Задачи для самостоятельного решения

66

67.

67

68. Задачи для осмысления

68

69. Площадь фигуры (задачи без параметра)

69

70. Площадь фигуры (задачи с параметром)

70

71. Площадь фигуры

Шабунин М.И., Прокофьев А.А.
71

72. Параметры в геометрических задачах

Задачи с параметрами в геометрии можно сгруппировать в задачи двух типов:
1) по содержанию – на построение, на вычисление;
2) по структуре – на задачи с «алгебраическим» и с «геометрическим»
параметром.
«Алгебраический» тип задач с параметрами в геометрии по своей сути
отличается от алгебраических задач только постановкой вопроса.
Например, при каком значении параметра, являющегося некоторым
измерением геометрической фигуры (высота, сторона, угол, площадь, объем и
т. д.), другая ее характеристика удовлетворяет некоторому заданному условию
(чему-то равна, минимальна или максимальна, находится в заданном
интервале).
«Геометрический» тип задач с параметрами – это многовариантные
геометрические задачи.
В обоих случаях значение параметра определяет:
количество возможных способов решений в зависимости от условия задачи;
количество возможных решений в зависимости от условия задачи;
количество решений в зависимости от области определения полученного
результата решения задачи.
72

73. Применение параметров в геометрии

73

74.

74

75.

75

76.

76

77.

77

78.

78

79. Параметрические уравнения отрезка

79

80. Параметрические уравнения отрезка

80

81. Классификация задач, решаемых функционально-графическими методами

1. К первому типу отнесем задачи, в условии которых спрашивается о
количестве решений уравнения или системы уравнений в зависимости от
значения параметра.
2. Ко второму типу отнесем задачи, в условии которых спрашивается о
необходимости нахождения значений параметра, при которых задача имеет
заданное количество решений (единственное, k решений, бесконечно много).
3. Третий тип представляют задачи, в которых необходимо получить решение
для всех значений параметра или для значений параметра из заданного
промежутка.
4. Четвертый тип представляют задач, в которых необходимо найти значения
параметра, при которых множество решений удовлетворяет заданным
условиям.
81

82. Печатные и электронные ресурсы

Школьные учебники.
Пособия для подготовки к ЕГЭ по математике.
Журналы «Математика в школе», «Математика
для школьников»,
«Математика», «Потенциал»
Сайты: alexlarin.net, abiturient.ru (МИЭТ),
mathus.ru/math/ , reshuege.ru,
ege-ok.ru/category/zadachi-s-parametrom/
82

83. Контакты

Спасибо за внимание!
[email protected]
05.12.14
83