Метод координат при решении геометрических задач

1. Метод координат при решении геометрических задач

МЕТОД КООРДИНАТ
ПРИ РЕШЕНИИ
ГЕОМЕТРИЧЕСКИХ
ЗАДАЧ

2. Рене Декарт (1596-1650)

РЕНЕ ДЕКАРТ (1596-1650)
Французский математик,
физик, философ,
создатель знаменитого
метода координат,
сторонник механизма с
физике, предтеча
рефлексологии.
По образованию юрист, но
юридической практикой
не занимался никогда.

3. Основные формулы

ОСНОВНЫЕ ФОРМУЛЫ
А( х1; у1 ), В( х2 ; у2 )
АВ ( х2 х1 ) ( у2 у1 )
х1 х 2
у1 у2
АМ МВ, хм
, ум
2
2
АВ х2 х1 ; у2 у1
2
2

4. Уравнение прямой

УРАВНЕНИЕ ПРЯМОЙ
ах bу с 0;
у kх b;
x m;
y n;
x 0;
y 0;

5. Взаимное расположение прямых на плоскости

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ
ПРЯМЫХ НА ПЛОСКОСТИ
у k1 х b1 ;
у k2 х b2 ;
k1 k2 ; b1 b2
пересекаются
k1 k 2
параллельны
k1 k2 1
совпадают
k1 k2 ; b1 b2
перпендикулярны

6. Уравнение окружности

УРАВНЕНИЕ ОКРУЖНОСТИ
( x a) ( y b) R
2
2
x y r
2
2
2
Y
2
1
0
1
X

7. Правила действий над векторами с заданными координатами.

1) Равные векторы имеют равные
координаты
Если
И
а х1 ; у1
a b
, то
b х2 ; у 2
х1 = х2; у1 = у2

8. Правила действий над векторами с заданными координатами.

2) Каждая координата суммы двух (и более)
векторов равна сумме соответствующих
координат этих векторов. (стр. 221)
3) Координаты противоположных векторов
противоположны.
4) Координаты разности двух векторов равны
разности соответствующих координат
вычитаемых векторов. (стр. 221)
5) Координаты коллинеарных векторов
пропорциональны.
6) Каждая координата произведения вектора на
число равна произведению соответствующей
координаты вектора на это число. (стр. 221)

9. Простейшие задачи в координатах

1. Нахождение координаты вектора
через координаты начала и конца
этого вектора.
Если точка А (х1;у1) и В(х2;у2),
то вектор АВ будет иметь координаты
{х2 – х1; у2 – у1}
Запомним, что из координаты конца вектора
вычитают координаты начала вектора

10. Простейшие задачи в координатах

2. Нахождение координаты
середины отрезка
Если точки А(x1 ; y1) и B(x2; y2),
то координаты (x;y) середины отрезка АВ
будут равны:
х = (х1+х2 ):2
у = (у1+у2):2

11. Простейшие задачи в координатах

3. Вычисление длины вектора по
его координатам.
Если а {х;у}, то | а | будет равна
| а | = √ х²+у²
(Доказательство на стр.226)

12. Простейшие задачи в координатах

4. Вычисление расстояния между
двумя точками
Если точки А(x1 ; y1) и B(x2; y2), то
|AB| будет равна:
| AB| = √ (х2-х1)² +(у2-у1)²

13.

y
Рассмотрим
задачу
А (2;3)
Дано: точки А(2 ; 3) и B(3; 1)
B(3; 1)
O
Найти : AB {?;?}
x
Решение:
AB {x2 -x1 ; y2- y1}
AB {3-2 ; 1-3} =>
Ответ : AB {1; -2}
AB {1; -2}

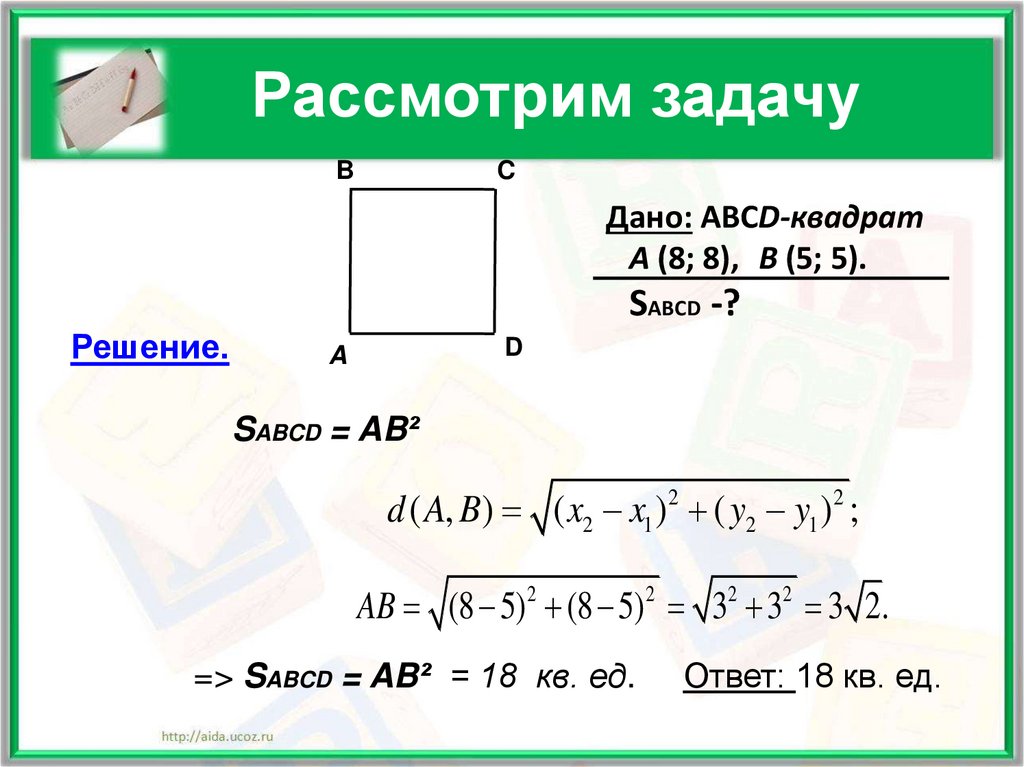
14. Рассмотрим задачу

B
C
Дано: АВСD-квадрат
A (8; 8), B (5; 5).
SABCD -?
Решение.
D
A
SABCD = AB²
d ( A, B) ( x2 x1 ) 2 ( y2 y1 ) 2 ;
AB (8 5)2 (8 5) 2 32 32 3 2.
=> SABCD = AB² = 18 кв. ед.
Ответ: 18 кв. ед.

15. Домашнее задание

Повторите материал по презентации,
решите № 941, 947 (а)

16. Уравнение окружности

Окружность - геометрическое место точек
плоскости, равноудаленных от некоторой,
которая называется центром окружности
Составим уравнение окружности с центром в точке
С (x0; y0) и радиусом R.
Пусть точка M (x; y) принадлежит окружности.
Тогда СM = R. =>
Квадрат расстояния между точками С и M равен
квадрату радиуса:
(x – x0 )² + (y – y0 )² = R²,
где
(x0 ; y0 ) -координаты центра окружности
(х ; y ) -координаты любой точки