Похожие презентации:
Методы решения геометрических задач. Планиметрия
1.
Методырешения геометрических задач
(планиметрия)
2. Основные методы решения геометрических задач
Метод дополнительных построенийМетод геометрических преобразований
Метод подобия
Метод площадей
Метод вспомогательной окружности
Метод геометрического видения
Метод координат
Векторный метод
3. Метод дополнительных построений
Разновидности:Продолжение отрезка (отрезков) на
определенное расстояние или до пересечения
с заданной прямой (прямыми).
Проведение прямой через две заданные точки.
Проведение через заданную точку прямой,
параллельной данной прямой, или
перпендикулярной данной прямой.
4. Метод геометрических преобразований
Разновидности:центральная симметрия,
осевая симметрия,
параллельный перенос,
поворот.
5. Метод площадей
Один из алгоритмов решения многихгеометрических задач основан на
использовании свойств площадей фигур.
6. Метод вспомогательной окружности
«Окружность – душа геометрии.Познайте окружность, и вы не
только познаете душу геометрии,
но и возвысите душу свою».
И.Ф. Шарыгин
7. Метод геометрического видения
Основывается на умениях видеть исопоставлять геометрические факты.
Обычно при решении не нужно выполнять
дополнительные построения и вычислений.
8. Метод координат
и векторный метод самые универсальные методы геометрии.Главное - удачно выбрать систему координат.
• I тип – задачи на нахождение зависимости
между элементами данной фигуры;
• II тип – задачи на составление уравнения
данной фигуры, если известны
характеристические свойства точек данной
фигуры.
9. Векторный метод
Типы задач, решаемых с помощьювекторного метода:
I тип – задачи, связанные с использованием
операций сложения векторов и умножения
вектора на число;
II тип – задачи с использованием операций
скалярного умножения векторов и
разложения вектора по базису.
10.
«Лучше решитьзадачу десятью
способами,
чем десять задач
одним».
Дьёрдь Пойя
11.
В треугольнике АВС биссектриса BЕ и медианаАD перпендикулярны и имеют одинаковую
длину, равную 4. Найти стороны треугольника
АВС.
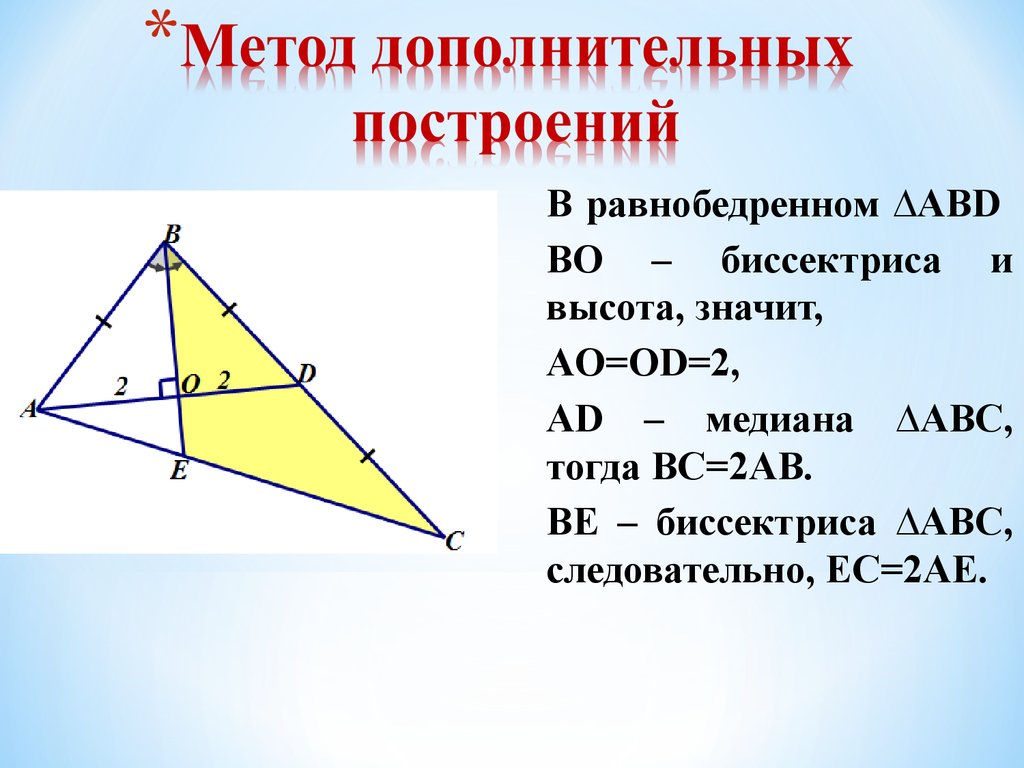
12. Метод дополнительных построений
В равнобедренном ∆ABDBO – биссектриса и
высота, значит,
AO=OD=2,
AD – медиана ∆ABС,
тогда BC=2AB.
BE – биссектриса ∆ABС,
следовательно, EC=2AE.
13.
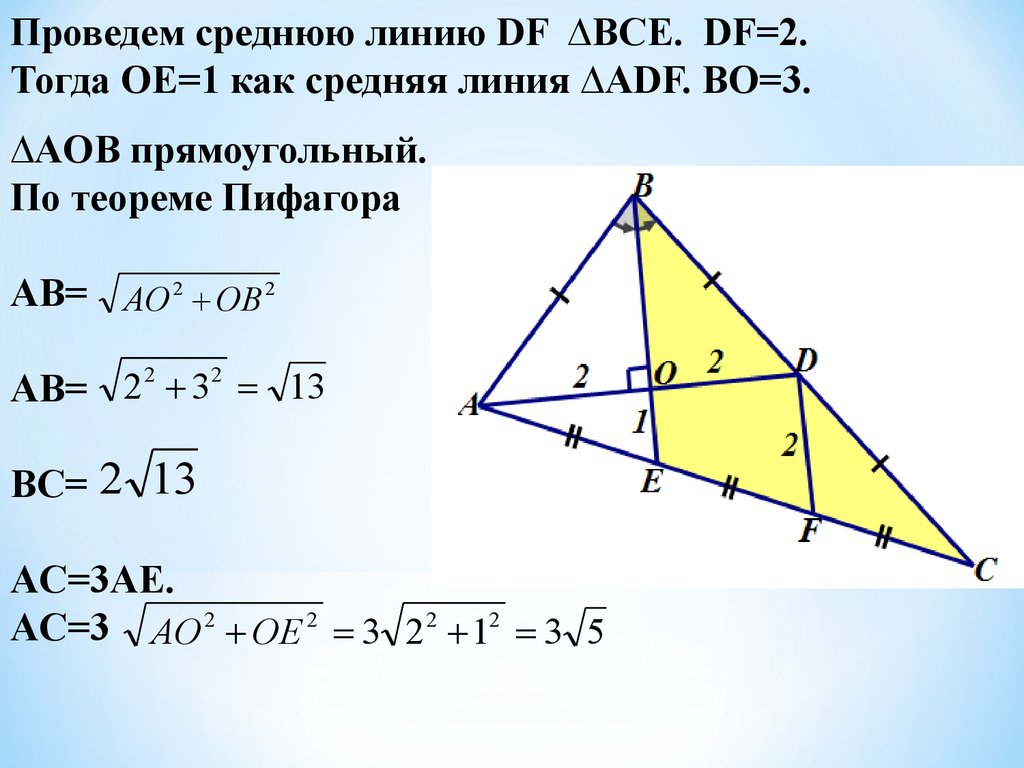
Проведем среднюю линию DF ∆BCE. DF=2.Тогда OE=1 как средняя линия ∆ADF. BO=3.
∆AOB прямоугольный.
По теореме Пифагора
AB= AO 2 OB 2
AB= 2 2 32 13
BC= 2 13
AC=3AE.
AC=3 AO 2 OE 2 3 2 2 12 3 5
14. Метод геометрических преобразований
Построим точку F,симметричную точке
С относительно BE:
F AB DE
∆ FBC равнобедренный,
Е – точка пересечения медиан ∆ FBC.
2
2
2
FE=EC= AC = FH EH 2 5, AC= 3 5.
3
BH=6, AD – средняя линия, значит BO=3. AB= 13
BC=2 13 .
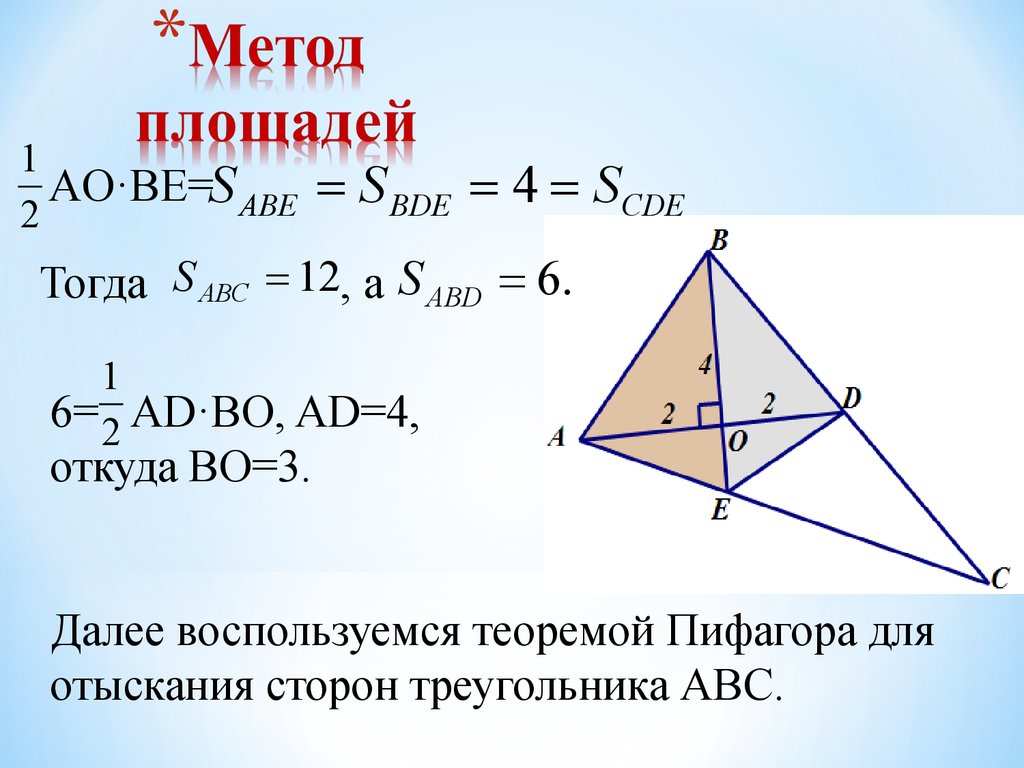
15. Метод площадей
1AO·BE=S ABE
2
S BDE 4 SCDE
Тогда S ABC 12, а S ABD 6.
1
6= 2 AD·BO, AD=4,
откуда BO=3.
Далее воспользуемся теоремой Пифагора для
отыскания сторон треугольника АВС.
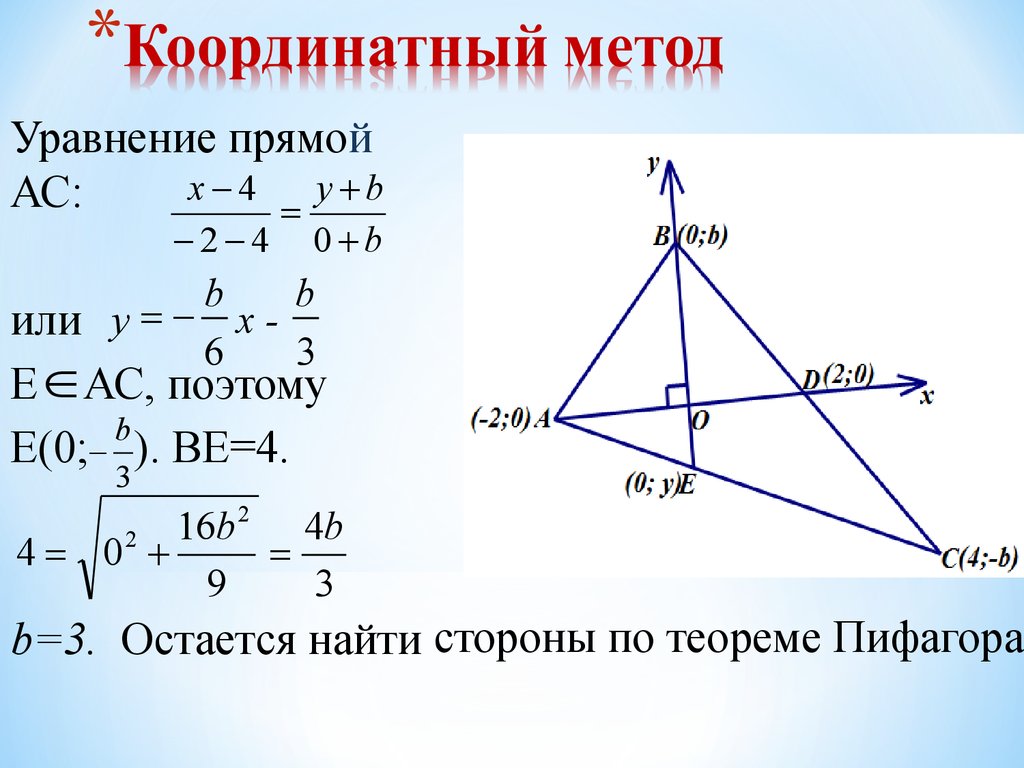
16. Координатный метод
Уравнение прямойx 4
y b
АС:
2 4
0 b
b
b
или y x 6
3
Е АС, поэтому
b
Е(0; ). ВЕ=4.
3
2
16
b
4b
2
4 0
9
3
b=3. Остается найти стороны по теореме Пифагора.
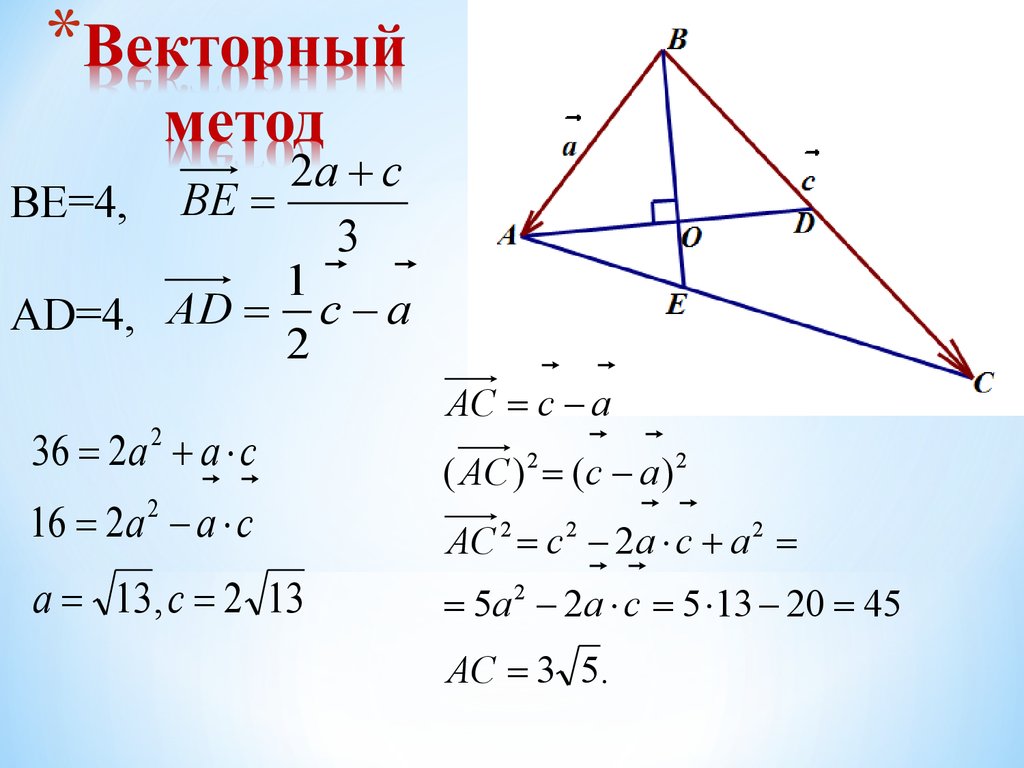
17. Векторный метод
2a cBE=4, BE
3
1
AD=4, AD с a
2
36 2а a c
2
16 2a a c
2
a 13 , c 2 13
AC c a
2
2
( AC ) (c a )
2
2
2
AC c 2a c a
2
5a 2a c 5 13 20 45
AC 3 5.












 Математика
Математика








