Похожие презентации:
Степенные функции
1.
2.
Степенными функцияминазывают функции вида
r
у х,
где r – любое
рациональное число
3.
mСтепенная функция у=х ,
где m - целое число
4.
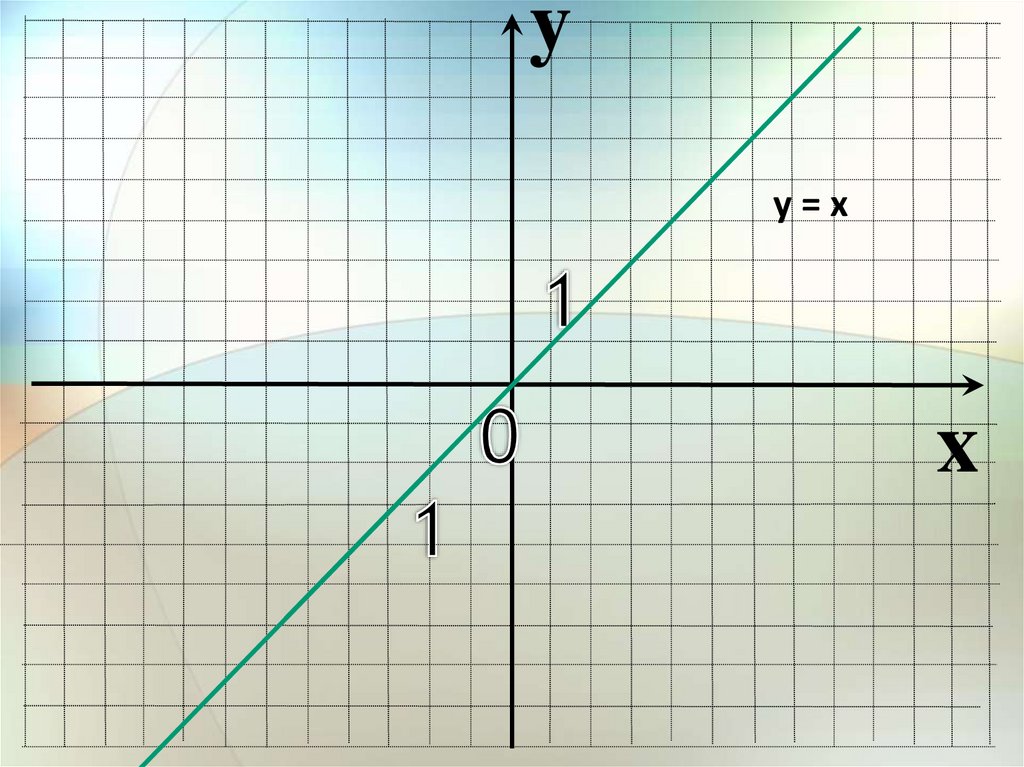
yу=х
x
5.
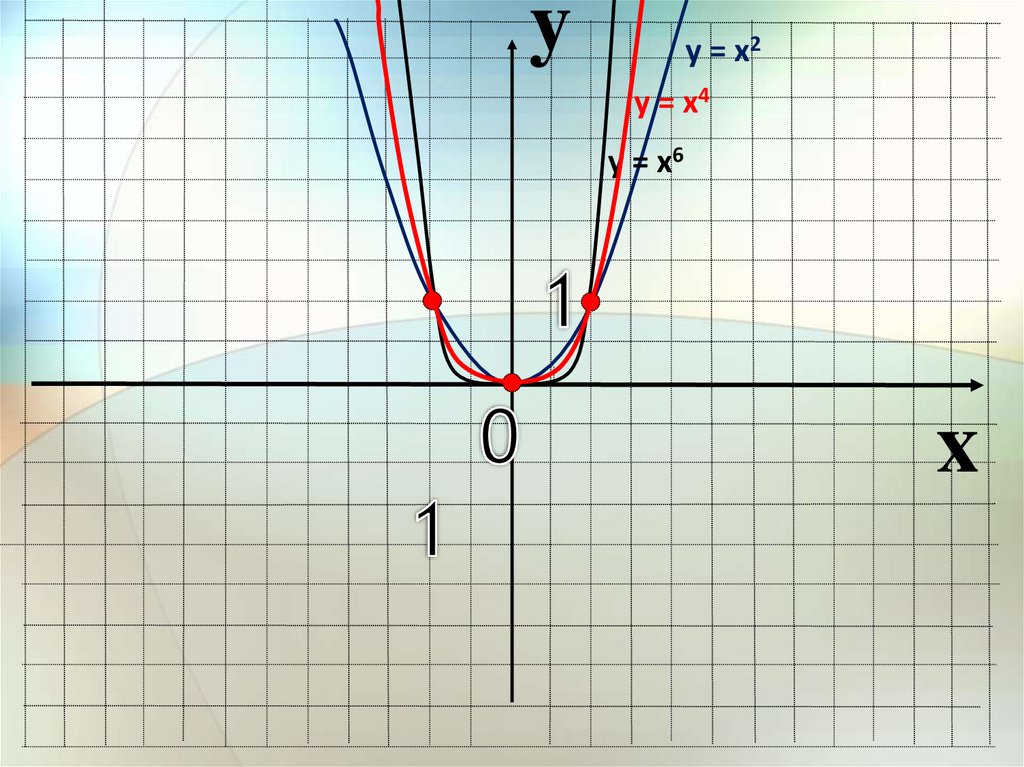
yу = х2
у = х4
у = х6
x
6.
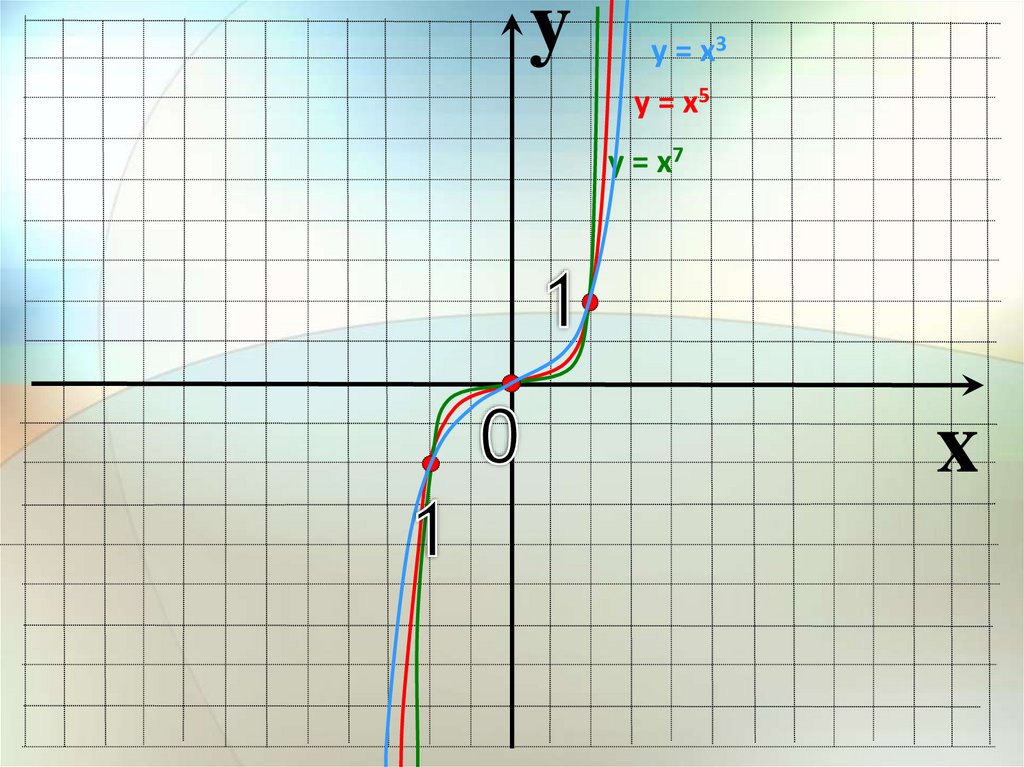
yу = х3
у = х5
у = х7
x
7.
yу = х-1
у = х-3
у = х-5
x
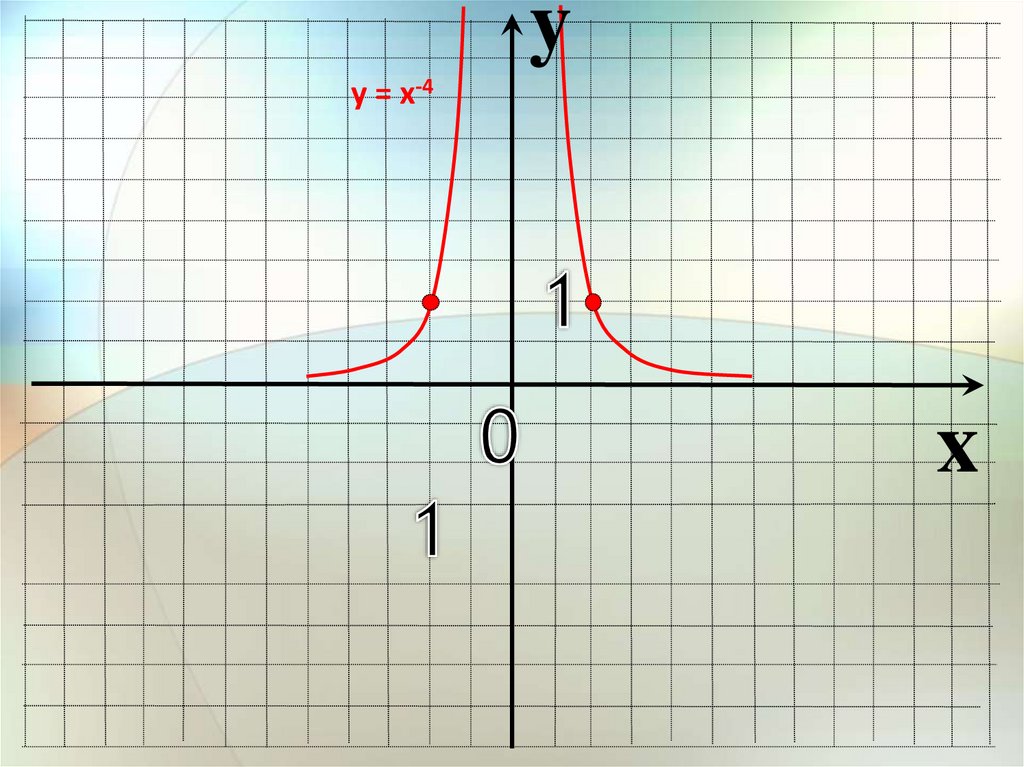
8.
yу = х-4
x
9.
у хm
1
n
m
n
10.
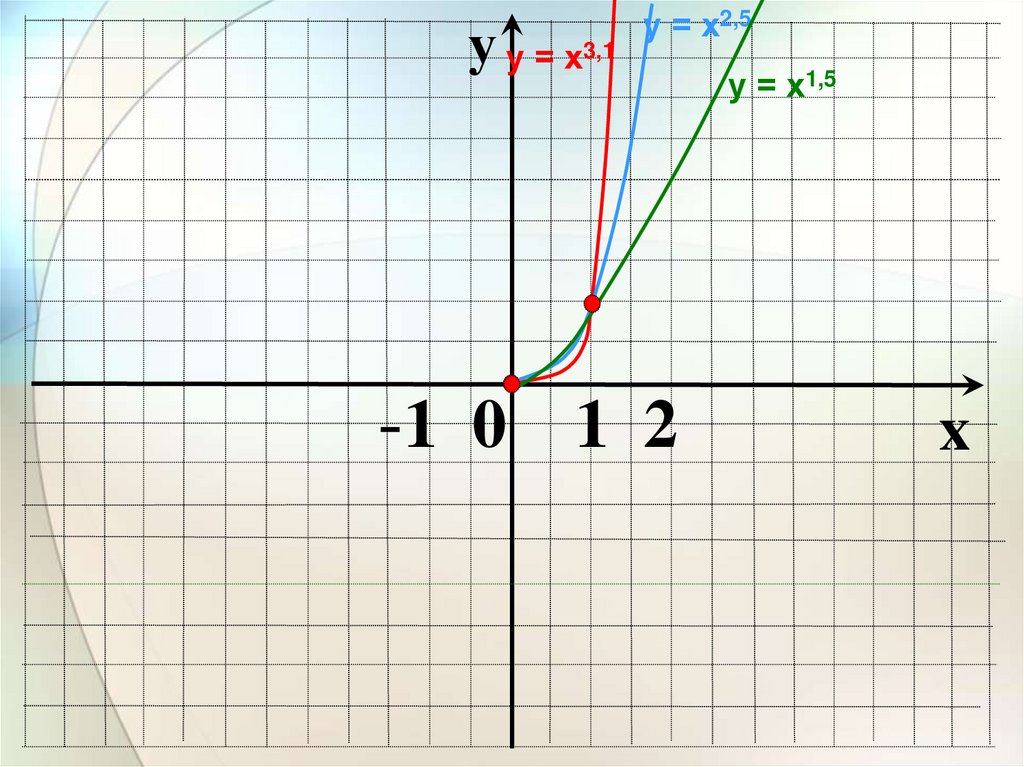
уу=х3,1
у = х2,5
-1 0 1 2
у = х1,5
x
11.
f ( x) xm
n
m
1
, где
n
• D( f ) 0;
• возрастает на [0; );
• унаим 0 ;
• непрерывна;
• Е( f ) 0;
12.
Выводы:m
n
• Особенности графика функции f ( x) x , где
m
1
n
: расположен в I координатной четверти,
проходит через точки (0;0), (1;1), похож на
«ветвь» параболы.
13.
Степенные функцииm
n
m
y x ,0 1,
n
их свойства и графики
14.
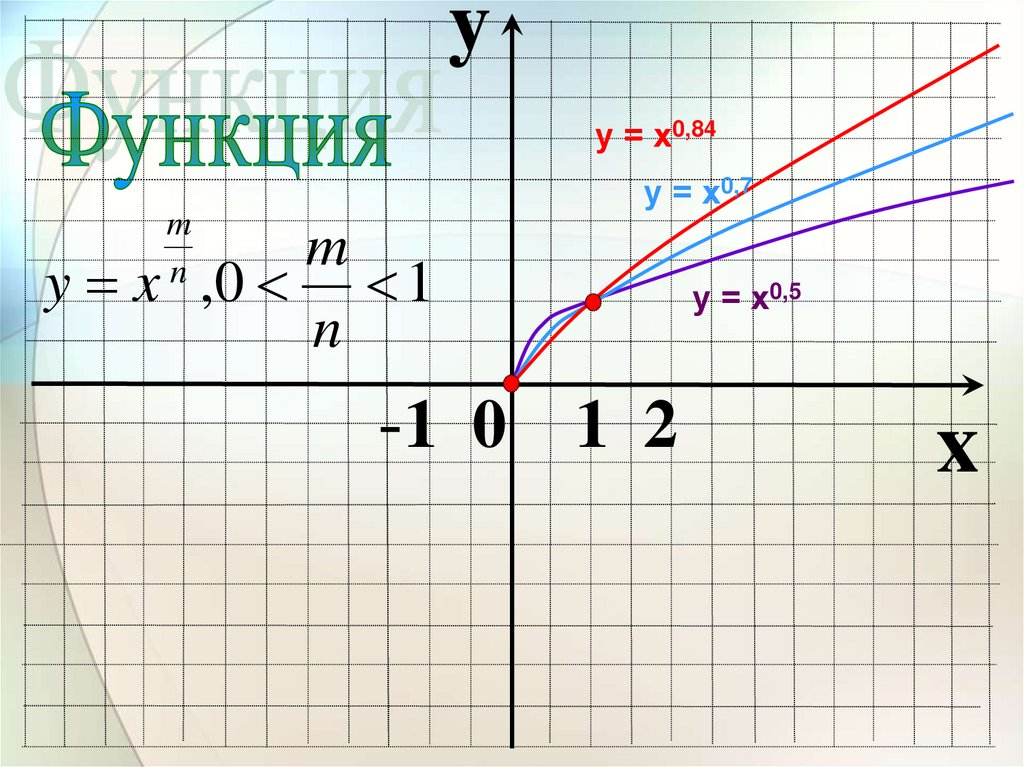
yу = х0,84
у = х0,7
m
n
m
y x ,0 1
n
-1 0 1 2
у = х0,5
x
15.
Выводы:m
n
• Особенности графика функции f ( x) x , где
0
m
1 :
n
расположен в I координатной четверти,
проходит через точки (0;0), (1;1), похож на
график функции f ( x)
такими же свойствами.
n
x , х 0 , обладает
16.
Степенные функцииy x
m
n
,
их свойства и графики
17.
yу = х-2,3
y x
m
n
х-1,3
у=
у = х-0,3
у = х-3,8
-1 0 1 2
x
18.
Выводы:• Особенности графика функции f ( x) x
m
n
:
расположен в I координатной четверти,
проходит через точки (0;0), (1;1),
похож на «ветвь» гиперболы.
График данной функции имеет горизонтальную
асимптоту у = 0 и вертикальную асимптоту х = 0.
19.
1. Решите уравнение4
3
x 2 x.
Решение.
1) Нетрудно подобрать один корень этого уравнения:
4
х = 1.
13 2 1 – верное равенство.
2) Т.к. степенная функция y x
4
3
возрастает, а линейная
функция y 2 x убывает, то других корней у
уравнения нет.
Ответ :
х =1.
20.
2). Найдите наименьшее и наибольшее значение функцииy x
5
2
на отрезке [1;2].
Решение:
Воспользуемся тем, что функция возрастает и,
следовательно, свои наименьшее и наибольшее значения
достигает соответственно в левом и правом концах
заданного промежутка, если концы промежутка
принадлежат самому промежутку.
5
2
yнаим. 1 15 1
5
2
yнаиб. 2 25 32 16 2 4 2
21.
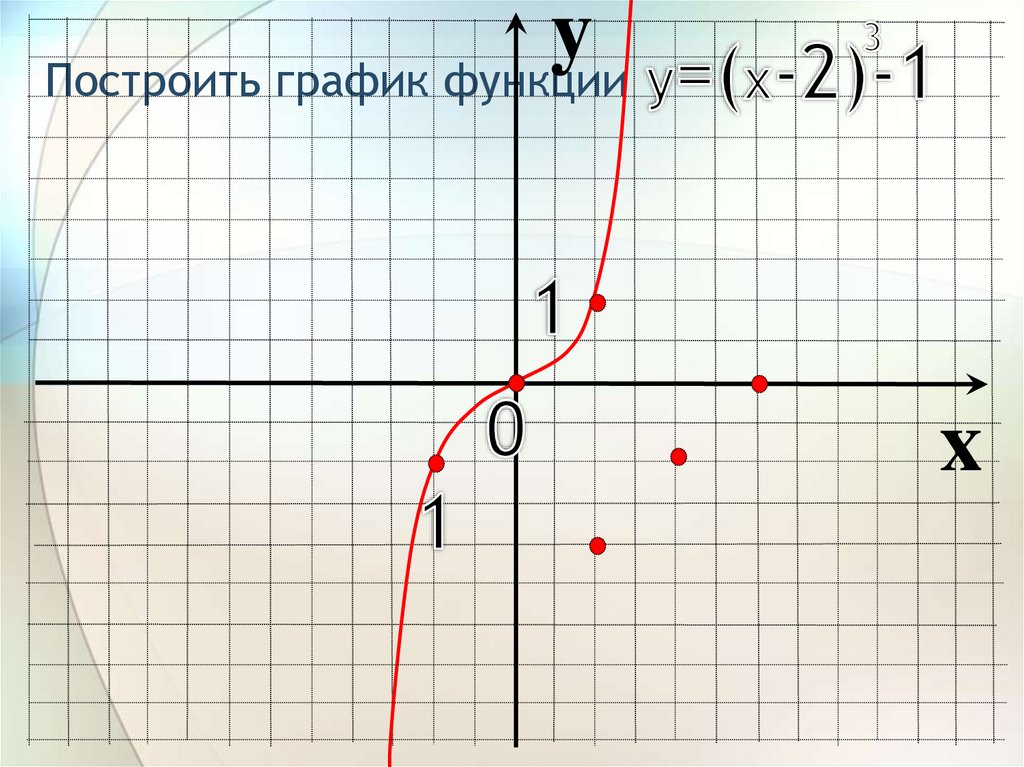
yПостроить график функции
x
22.
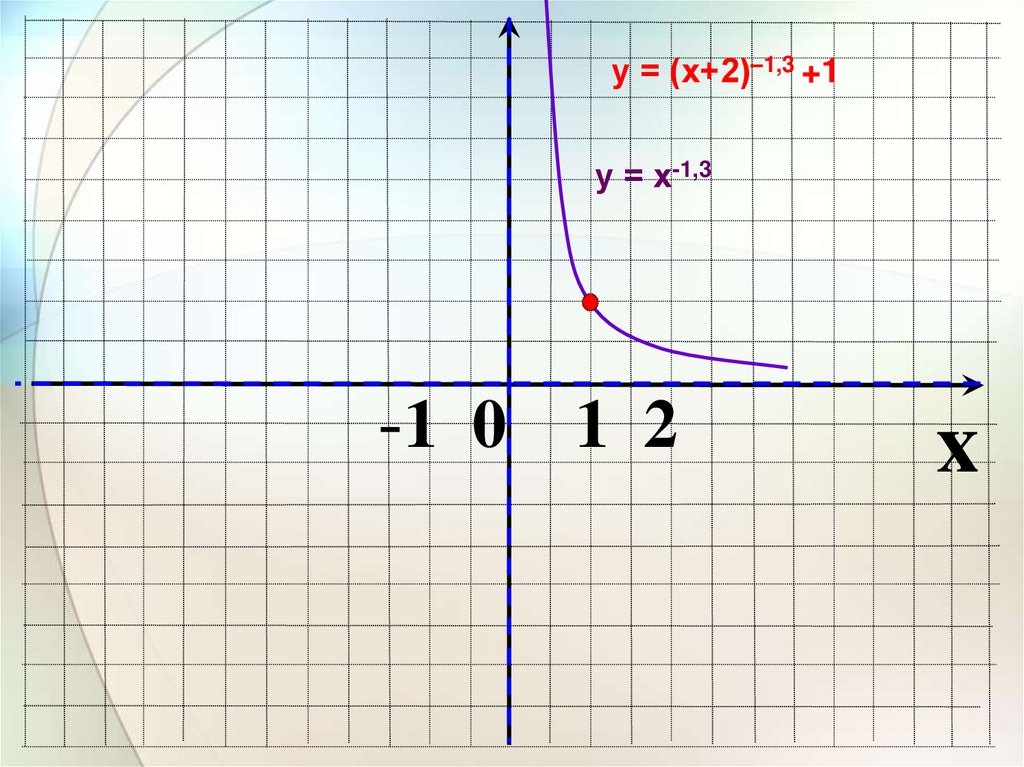
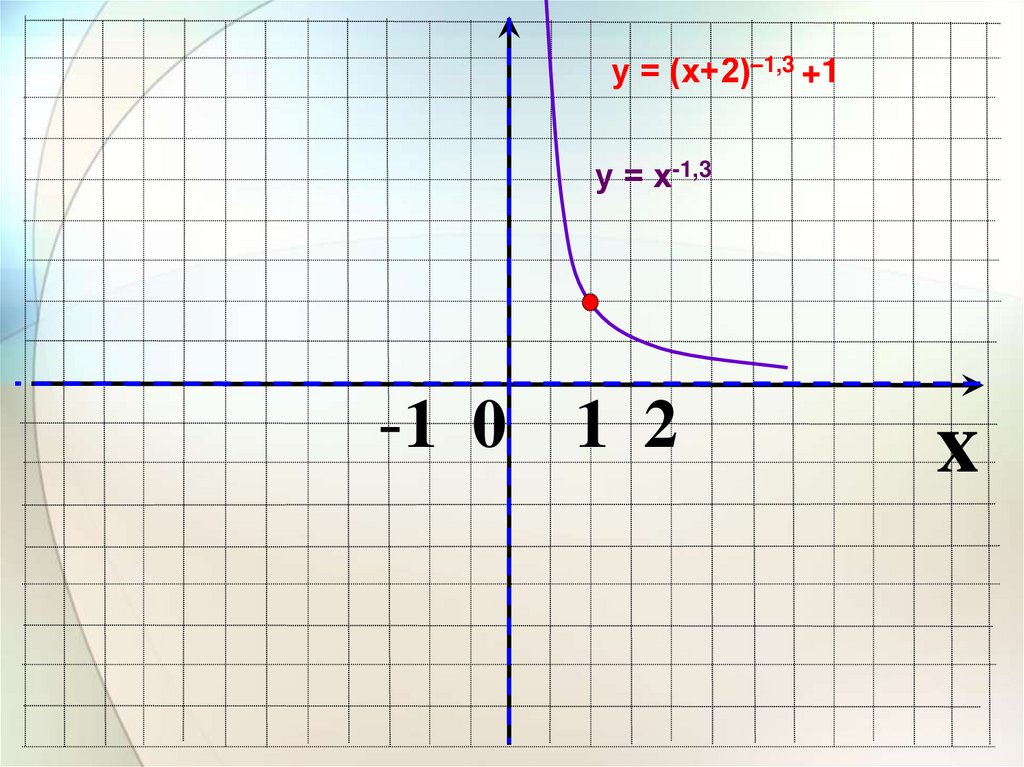
у = (х+2)–1,3 +1у = х-1,3
-1 0 1 2
x
23.
у = (х+2)–1,3 +1у = х-1,3
-1 0 1 2
x
24.
Задания для самостоятельного решения• Решите уравнение
3
2
1
х 2 .
х
• Постройте и прочитайте график функции
х 2 , если _ х 0,
2
3
у х , если 0 x 1,
1
, х 1.
x
• Решите неравенство х
1
4
х .
3















 Математика
Математика








