Похожие презентации:
Степенные функции, их свойства и графики
1.
2.
Степенные функции,их свойства и
графики
3.
Цель урока:обобщить и систематизировать знания и умения
по теме «Степенные функции, их свойства и
графики»
4.
Задачи:видеть график степенной функции по формуле
определять по графику функцию
уметь анализировать график
уметь решать уравнения, неравенства, системы
уравнений с помощью графиков и свойств
степенной функции
развивать навыки мыслительной деятельности,
математической зоркости
умение работать в сообществе
5.
Степенными функцияминазываются функции вида
r
у = х , где r – заданное
рациональное число
6.
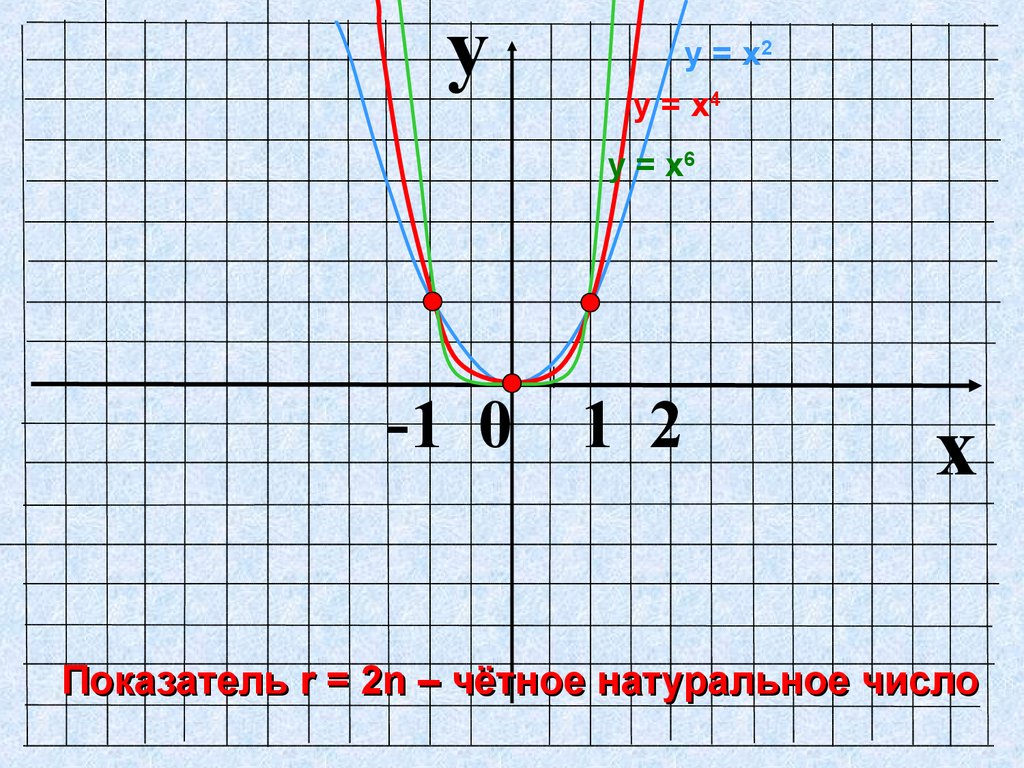
yу = х2
у = х4
у = х6
-1 0 1 2
x
Показатель r = 2n – чётное натуральное число
7.
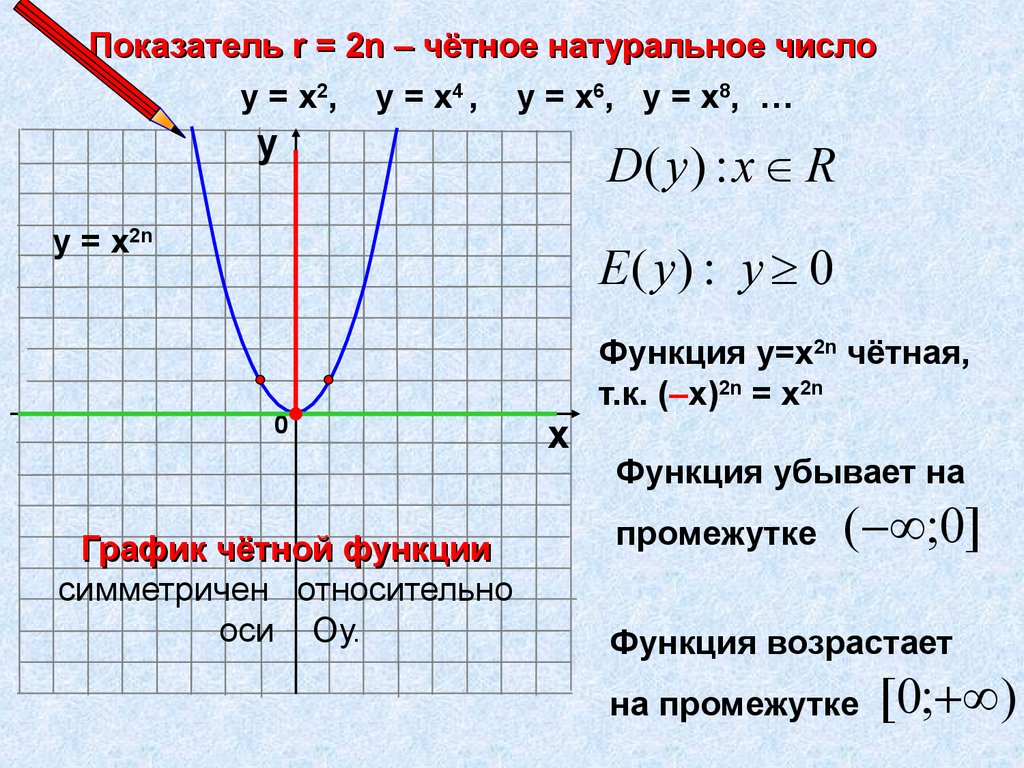
Показатель r = 2n – чётное натуральное числоу = х2 , у = х 4 , у = х6 , у = х 8 , …
у
D( y ) : x R
у = х2n
Е ( y) : у 0
0
График чётной функции
симметричен относительно
оси Оу.
х
Функция у=х2n чётная,
т.к. (–х)2n = х2n
Функция убывает на
промежутке
( ;0]
Функция возрастает
на промежутке
[0; )
8.
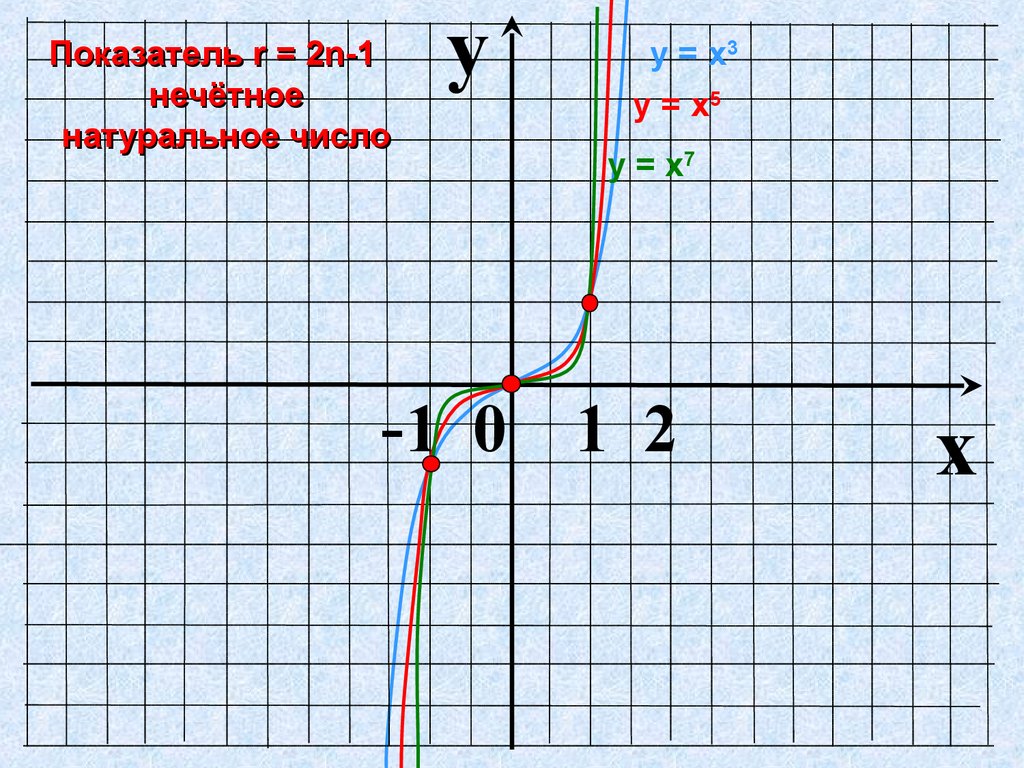
Показатель r = 2n-1нечётное
натуральное число
y
у = х3
у = х5
у = х7
-1 0 1 2
x
9.
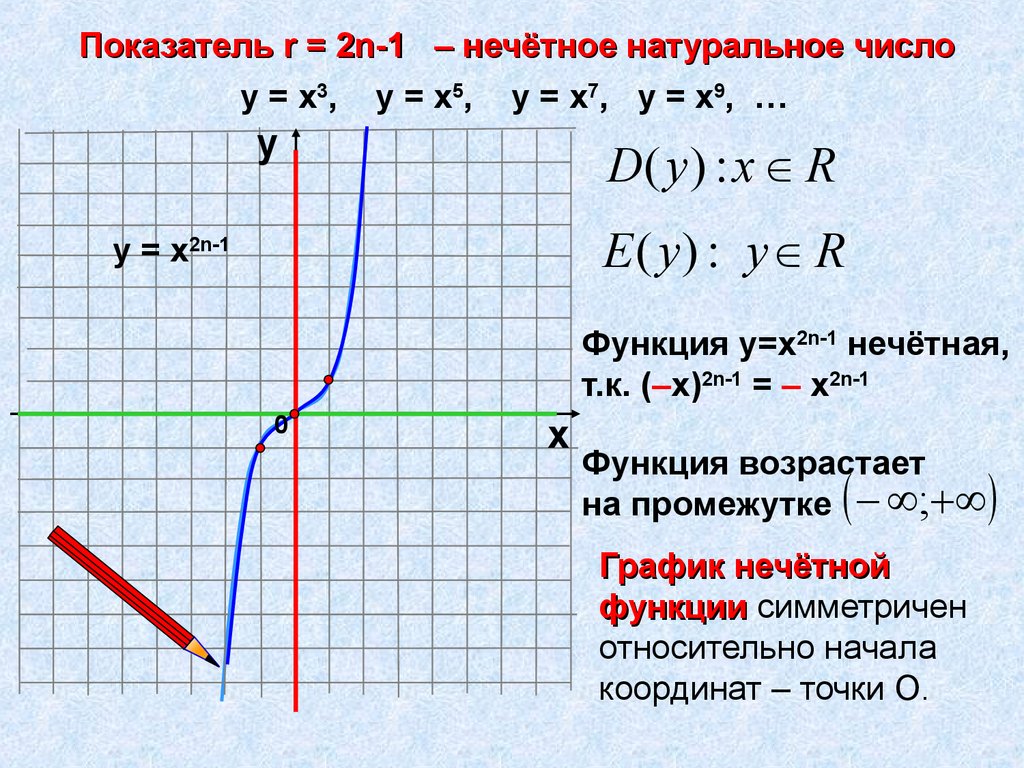
Показатель r = 2n-1 – нечётное натуральное числоу = х3 , у = х 5 , у = х7 , у = х 9 , …
у
D( y ) : x R
Е ( y) : у R
у = х2n-1
Функция у=х2n-1 нечётная,
т.к. (–х)2n-1 = – х2n-1
0
х
Функция возрастает
на промежутке ;
График нечётной
функции симметричен
относительно начала
координат – точки О.
10.
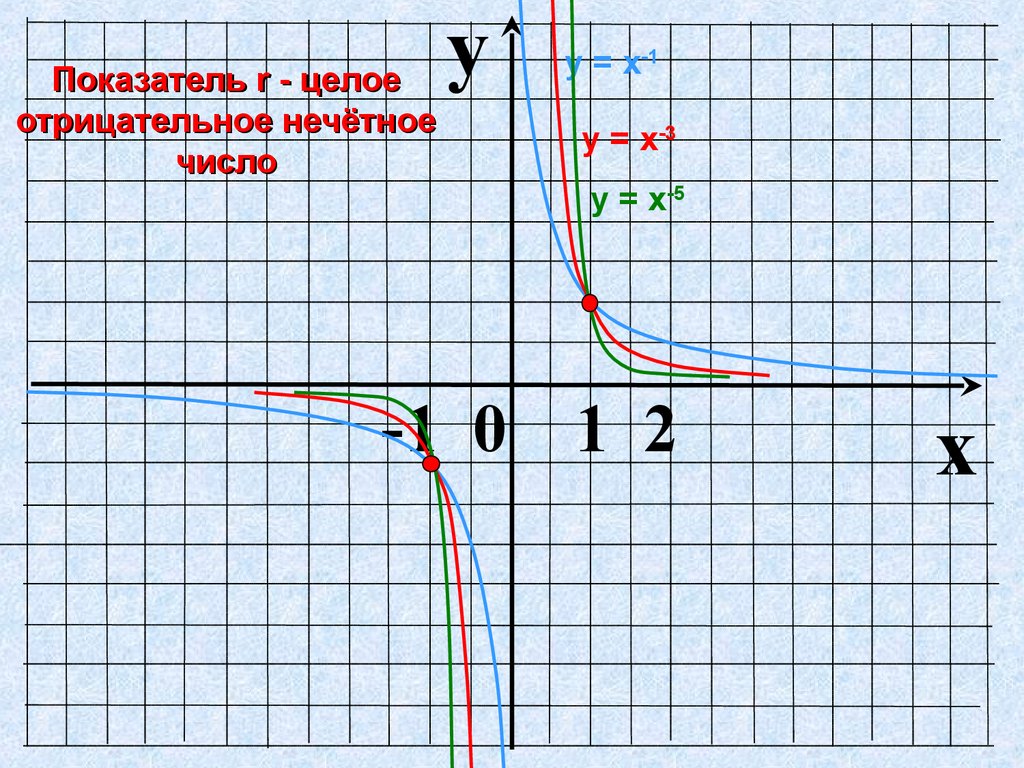
Показатель r - целоеотрицательное нечётное
число
y
у = х-1
у = х-3
у = х-5
-1 0 1 2
x
11.
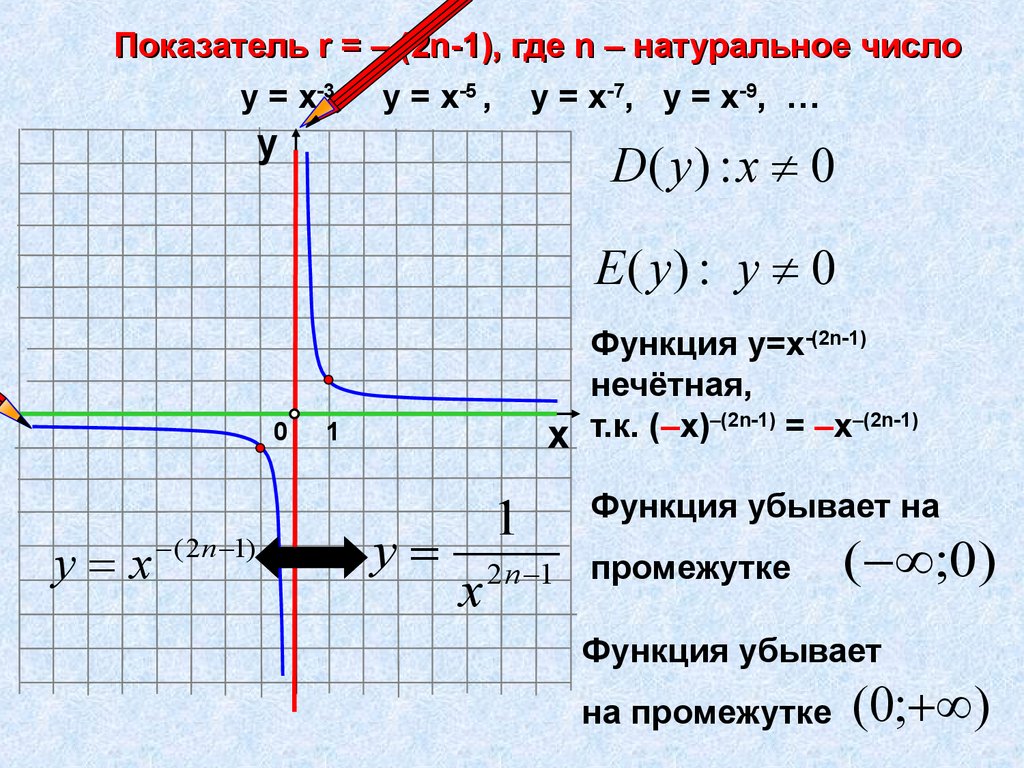
Показатель r = – (2n-1), где n – натуральное числоу = х-3, у = х-5 , у = х-7, у = х-9, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
( 2 n 1)
Функция у=х-(2n-1)
нечётная,
–(2n-1)
= –х–(2n-1)
х т.к. (–х)
1
y
х
1
Функция убывает на
2 n 1
промежутке
( ;0)
Функция убывает
на промежутке
(0; )
12.
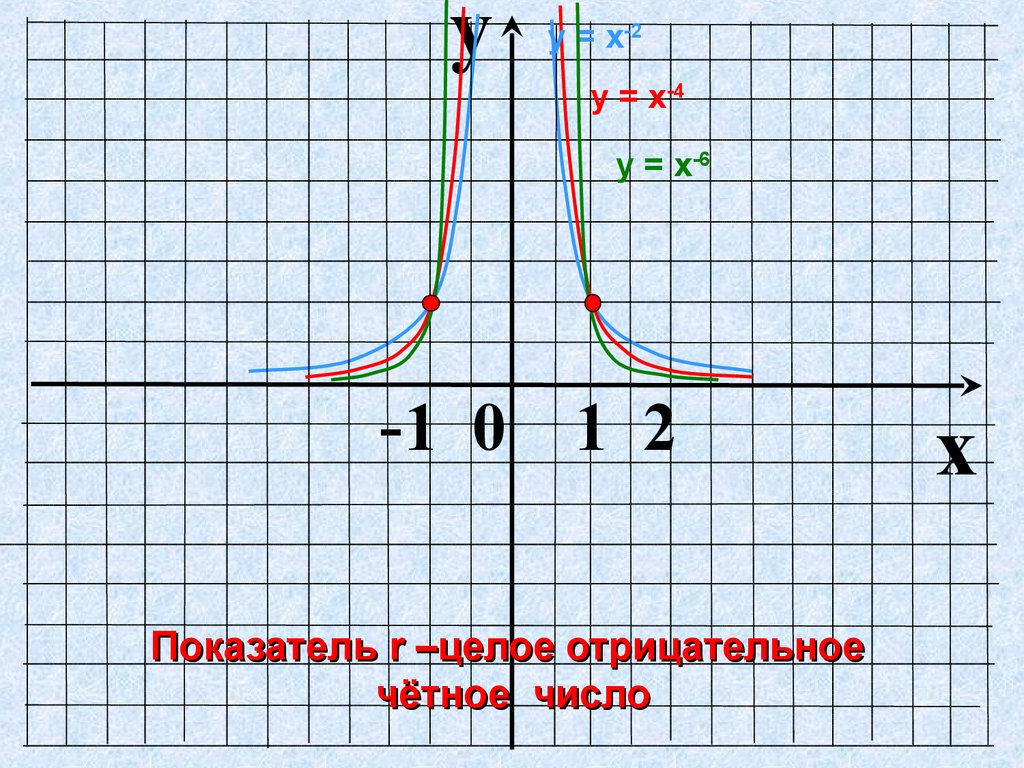
yу = х-2
у = х-4
у = х-6
-1 0 1 2
Показатель r –целое отрицательное
чётное число
x
13.
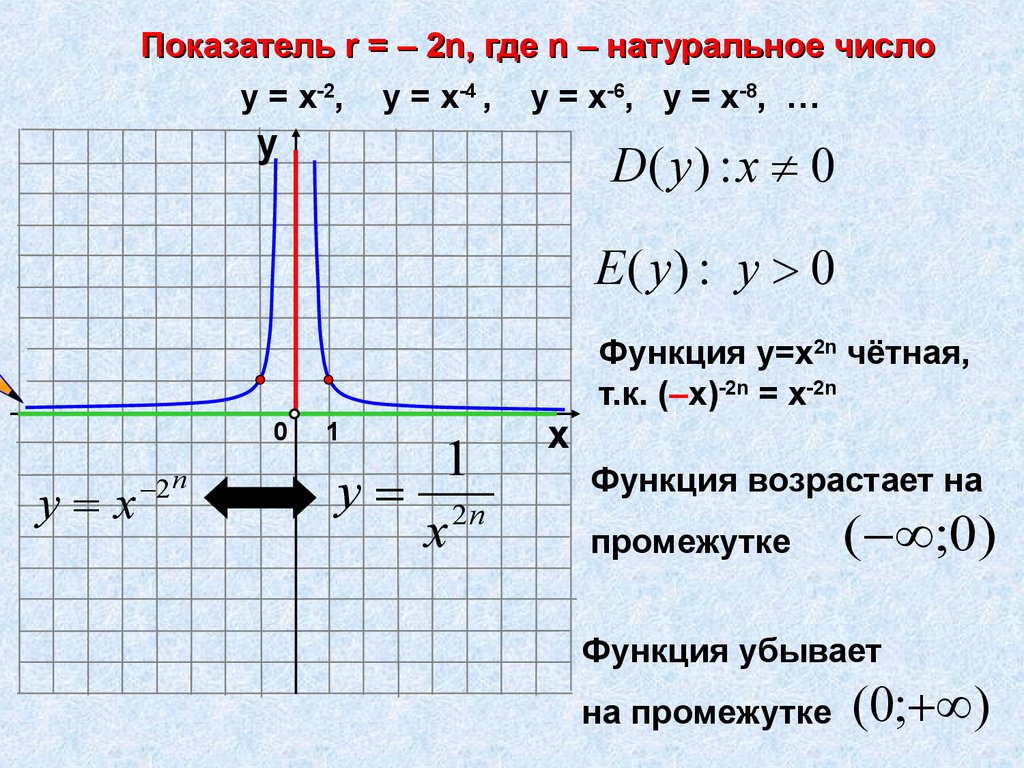
Показатель r = – 2n, где n – натуральное числоу = х-2, у = х-4 , у = х-6, у = х-8, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
2 n
1
1
y 2n
х
х
Функция у=х2n чётная,
т.к. (–х)-2n = х-2n
Функция возрастает на
промежутке
( ;0)
Функция убывает
на промежутке
(0; )
14.
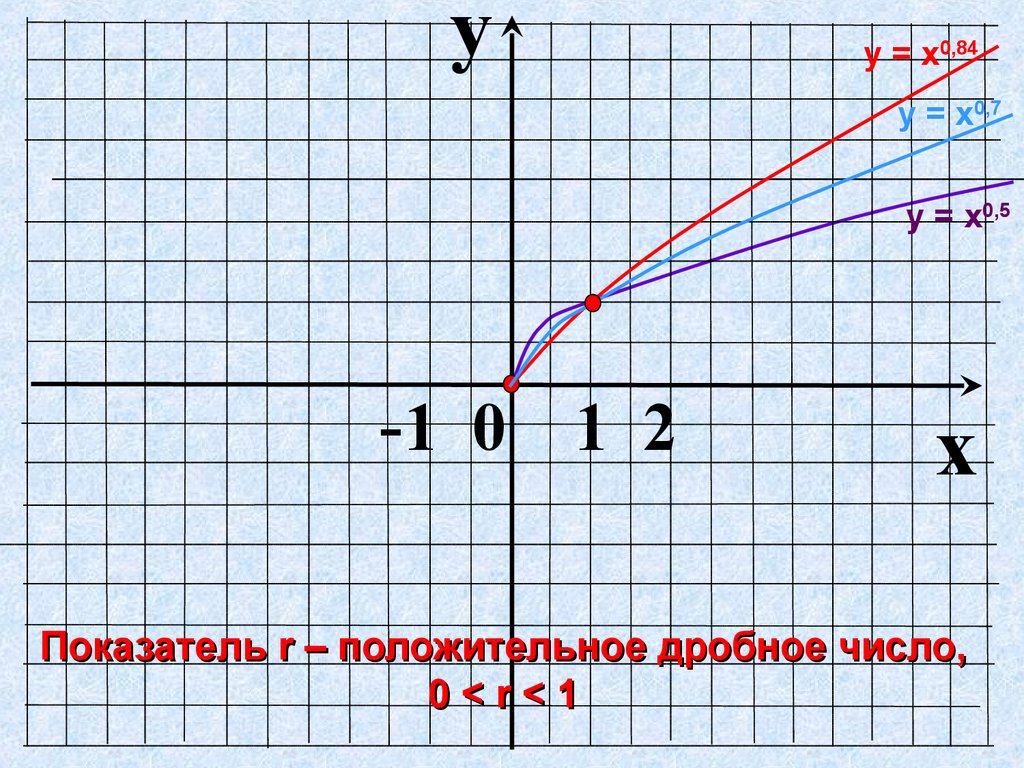
yу = х0,84
у = х0,7
у = х0,5
-1 0 1 2
x
Показатель r – положительное дробное число,
0<r<1
15.
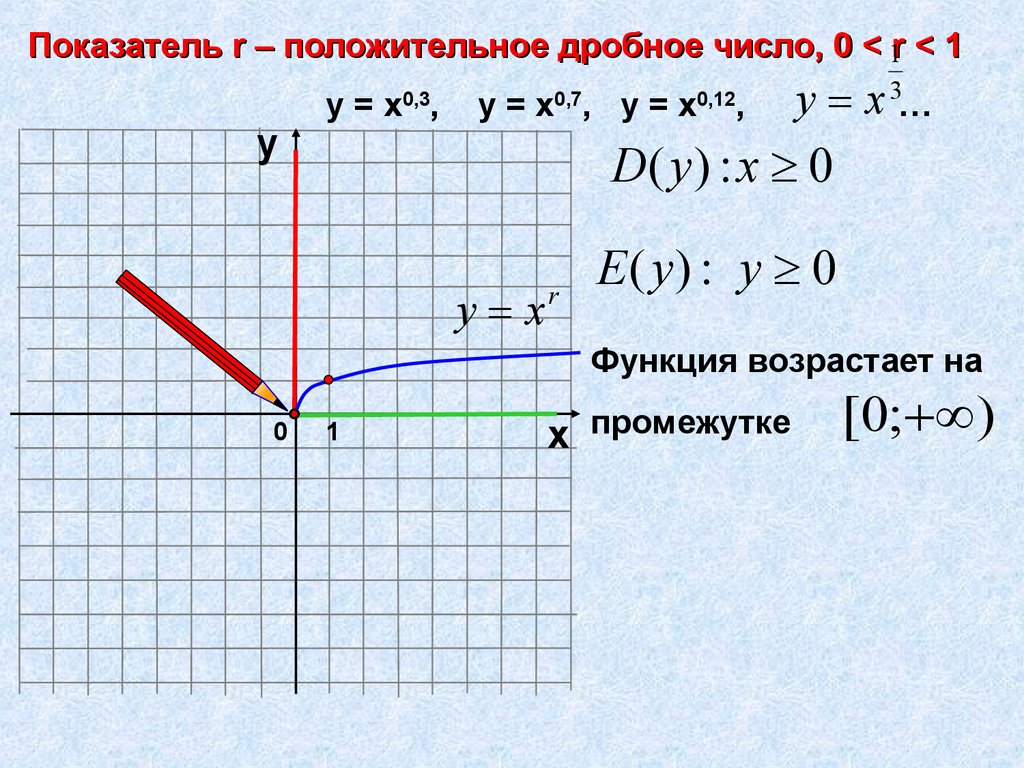
Показатель r – положительное дробное число, 0 < 1r < 1у
у = х0,3,
у = х0,7, у = х0,12,
у х 3…
D( y ) : x 0
у х
r
Е ( y) : у 0
Функция возрастает на
0
1
х промежутке
[0; )
16.
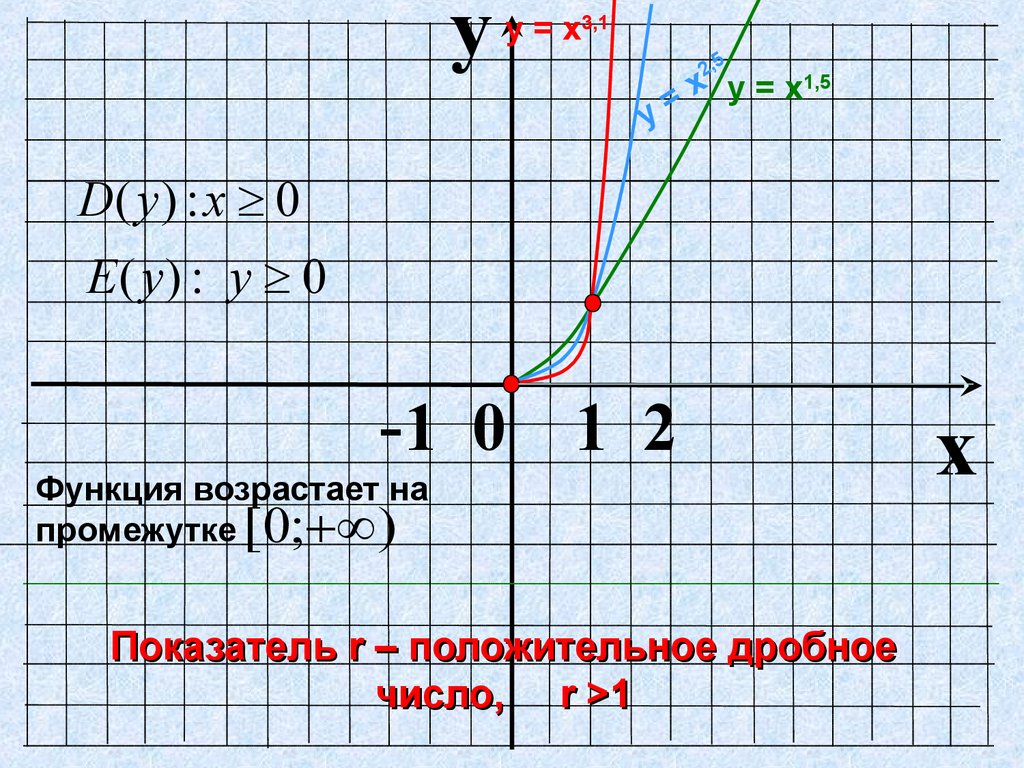
yу = х3,1
2, 5
у
1,5
х
у
=
х
=
D( y ) : x 0
Е ( y) : у 0
-1 0 1 2
Функция возрастает на
промежутке [0; )
Показатель r – положительное дробное
число, r >1
x
17.
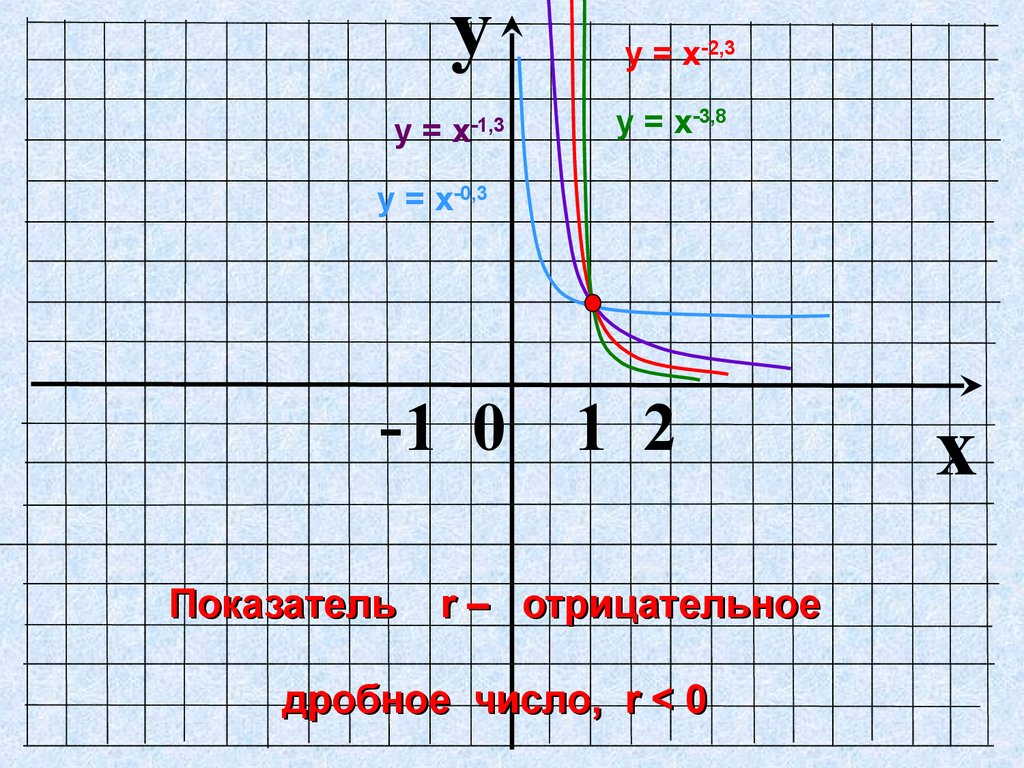
yу = х-1,3
у = х-2,3
у = х-3,8
у = х-0,3
-1 0 1 2
Показатель
r – отрицательное
дробное число, r < 0
x
18.
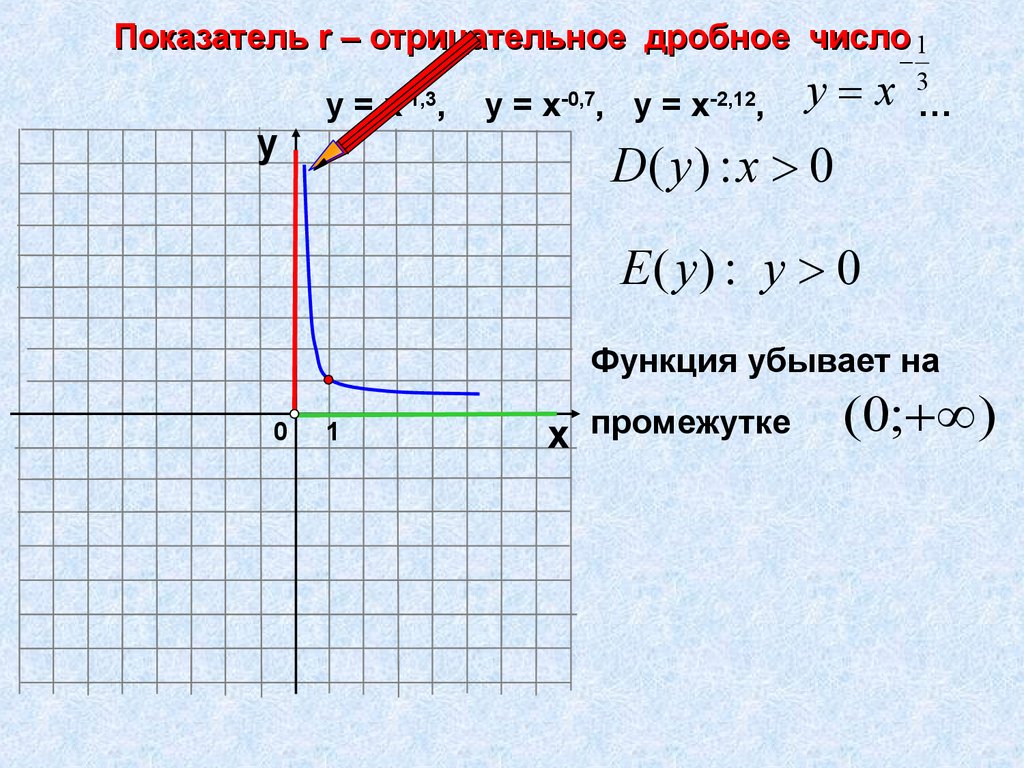
Показатель r – отрицательное дробное число 1у
у=х
-1,3
,
у=х
-0,7
, у=х
-2,12
,
у х
3
…
D( y ) : x 0
Е ( y) : у 0
Функция убывает на
0
1
х промежутке
(0; )
19.
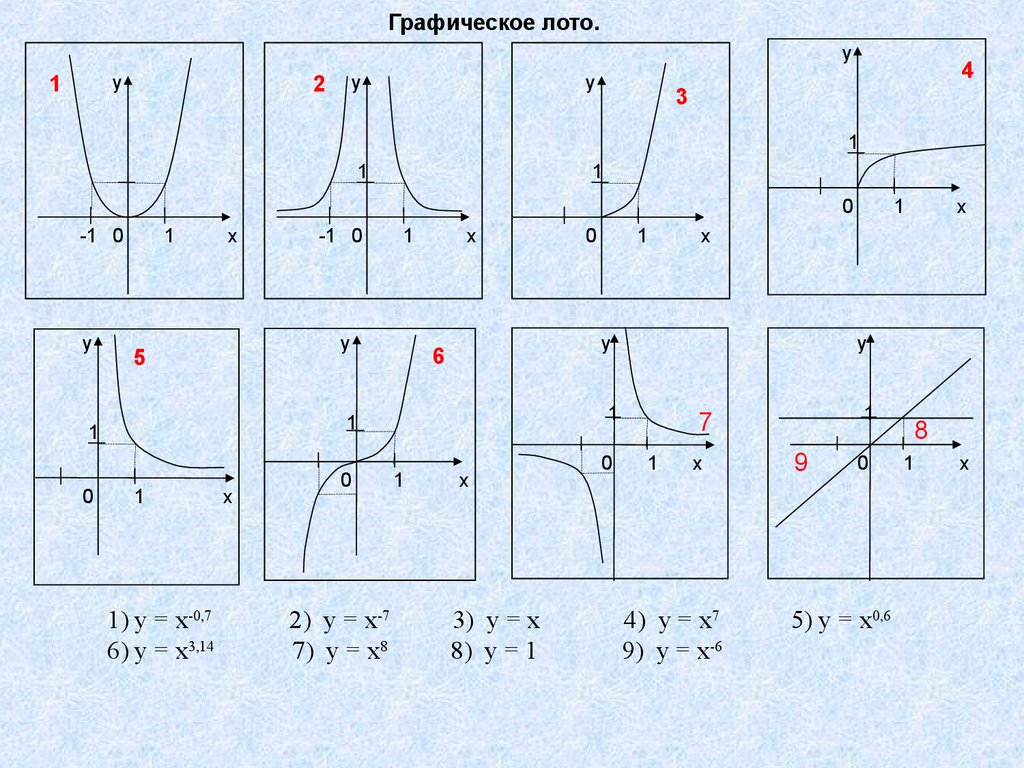
Графическое лото.у
у
1
у
2
у
4
3
1
1
1
0
-1 0
у
1
х
1
у
5
х
1
1) у = х-0,7
6) у = х3,14
х
0
2) у = х-7
7) у = х8
0
1
у
1
1
х
3) у = х
8) у = 1
0
х
х
у
6
1
1
0
-1 0
1
1
7
1
х
4) у = х7
9) у = х-6
9
0
5) у = х0,6
8
1
х
20.
ПРАВИЛЬНЫЙ ОТВЕТ:796 514 283
21.
уу х
у
х
=
у
х
=
у
у х
0
1
4
3
1
3
х
0
1
х
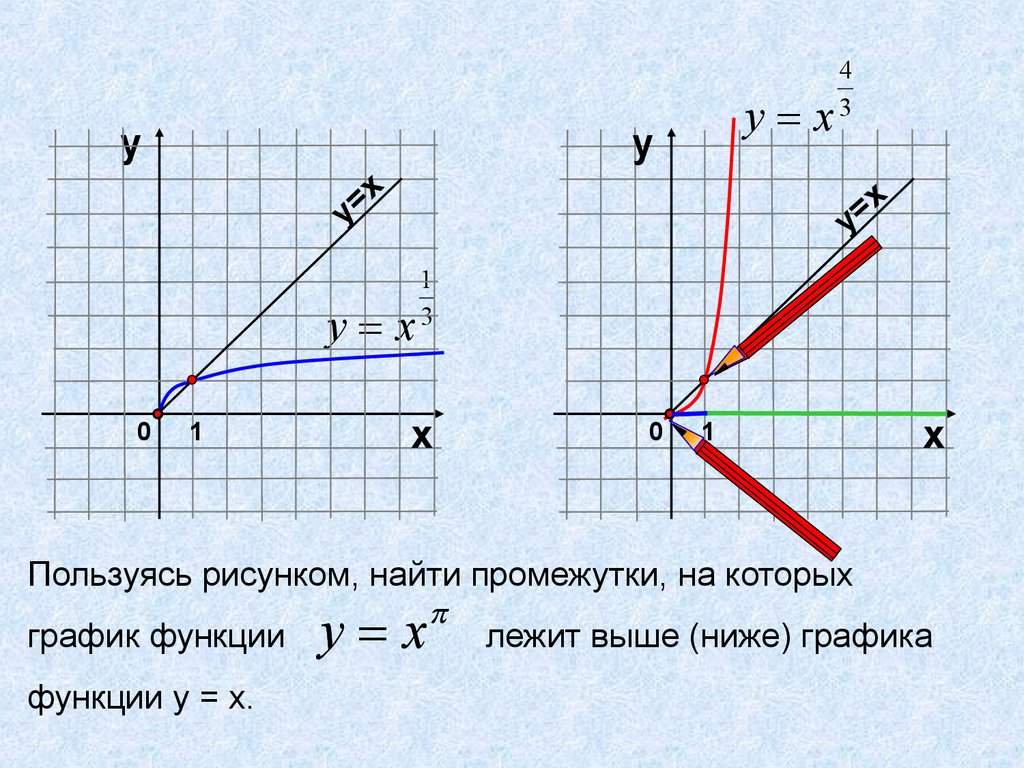
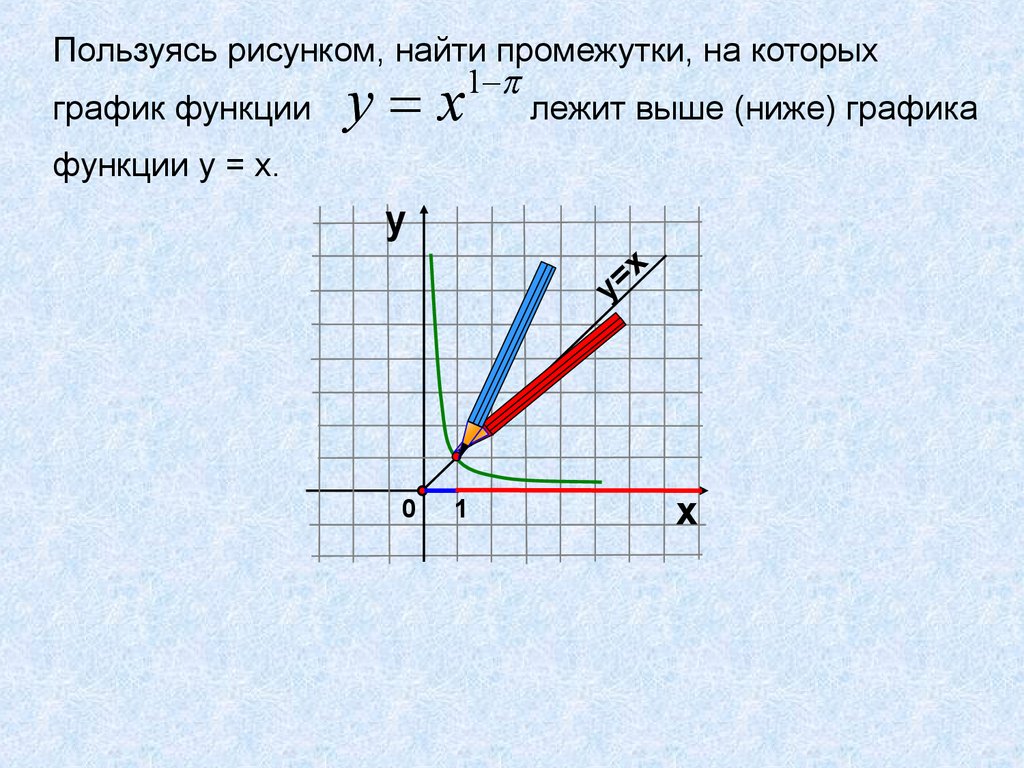
Пользуясь рисунком, найти промежутки, на которых
график функции у х
лежит выше (ниже) графика
функции у = х.
22.
уу х
у
х
=
у
х
=
у
у х
0
1
4
3
1
3
х
0
1
х
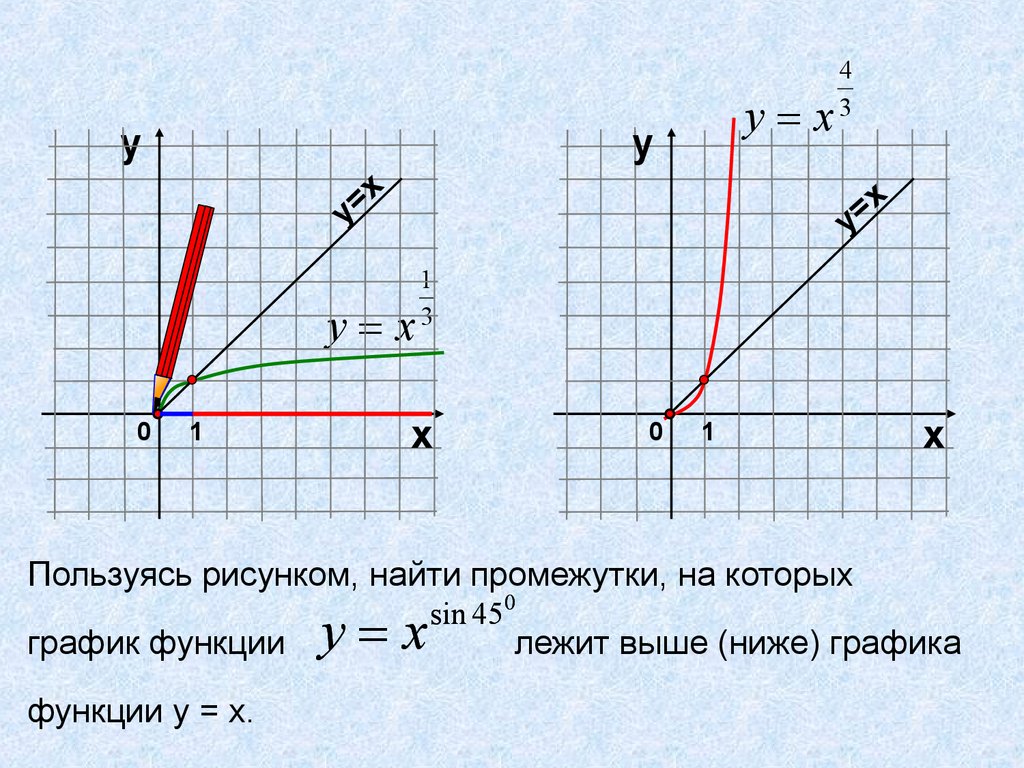
Пользуясь рисунком, найти промежутки, на которых
график функции
функции у = х.
у х
sin 450
лежит выше (ниже) графика
23.
Пользуясь рисунком, найти промежутки, на которых1
график функции
лежит выше (ниже) графика
у х
функции у = х.
у
х
=
у
0
1
х
24.
Преобразованияграфиков
степенных функций
25.
Как построить график функцииy = f(x + l),
если известен график функции
y = f(x)
26.
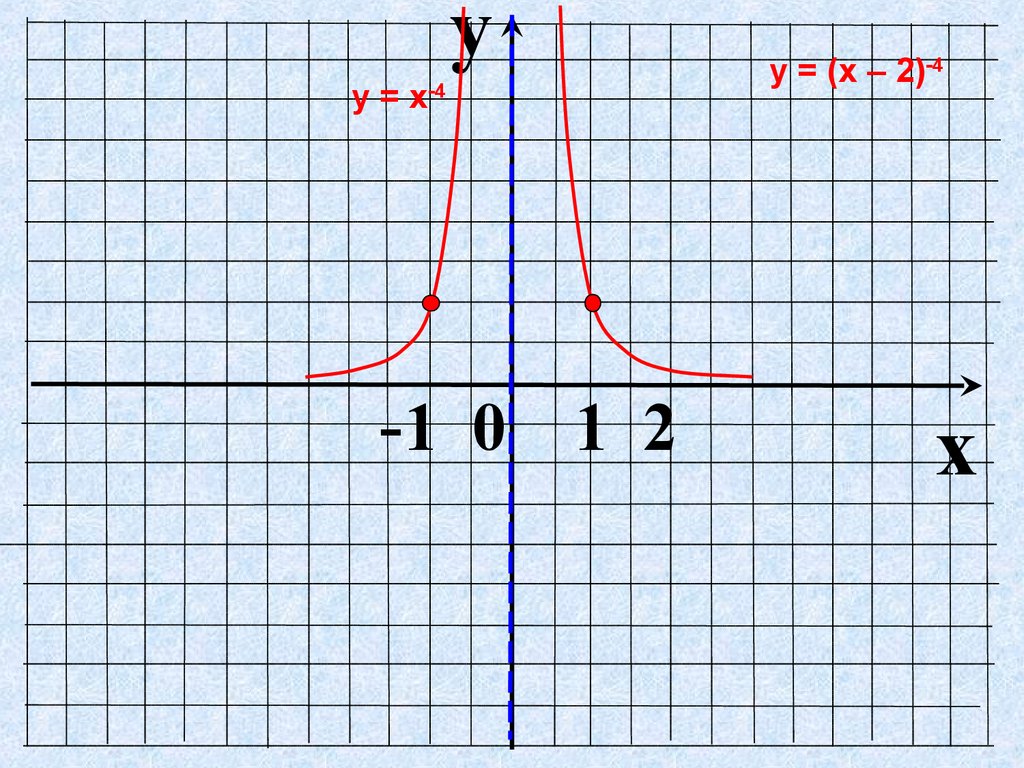
yу = х-4
-1 0 1 2
у = (х – 2)-4
x
27.
Как построить график функцииy = f(x) + m,
если известен график функции
y = f(x)
28.
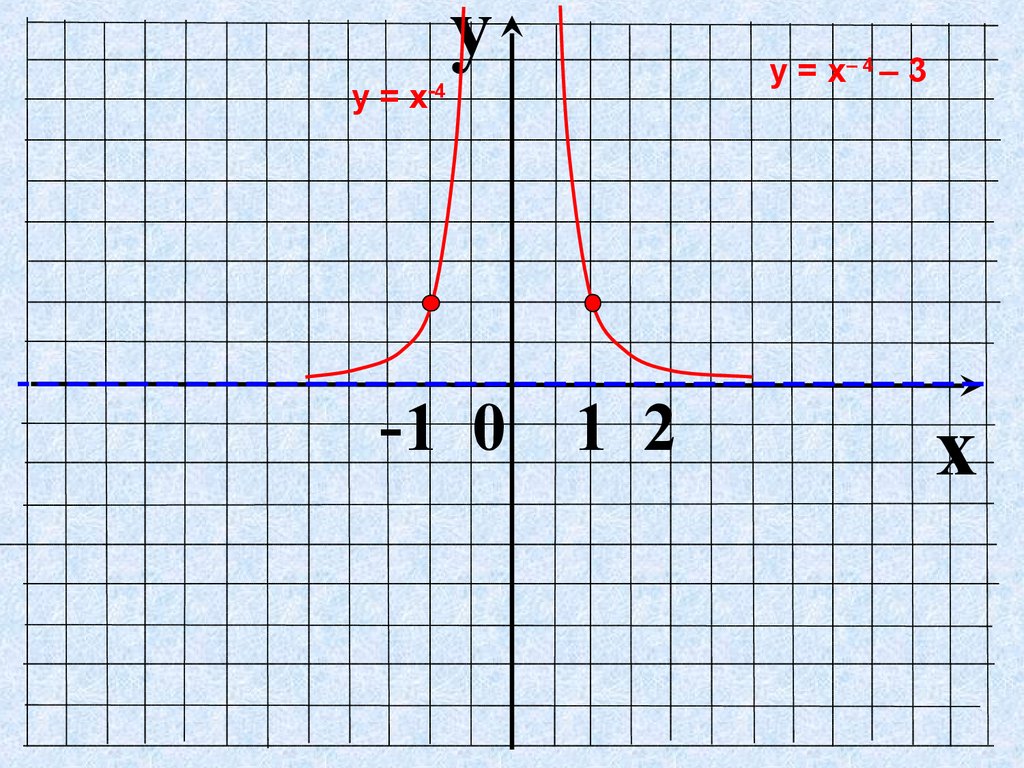
yу = х-4
-1 0 1 2
у = х– 4 – 3
x
29.
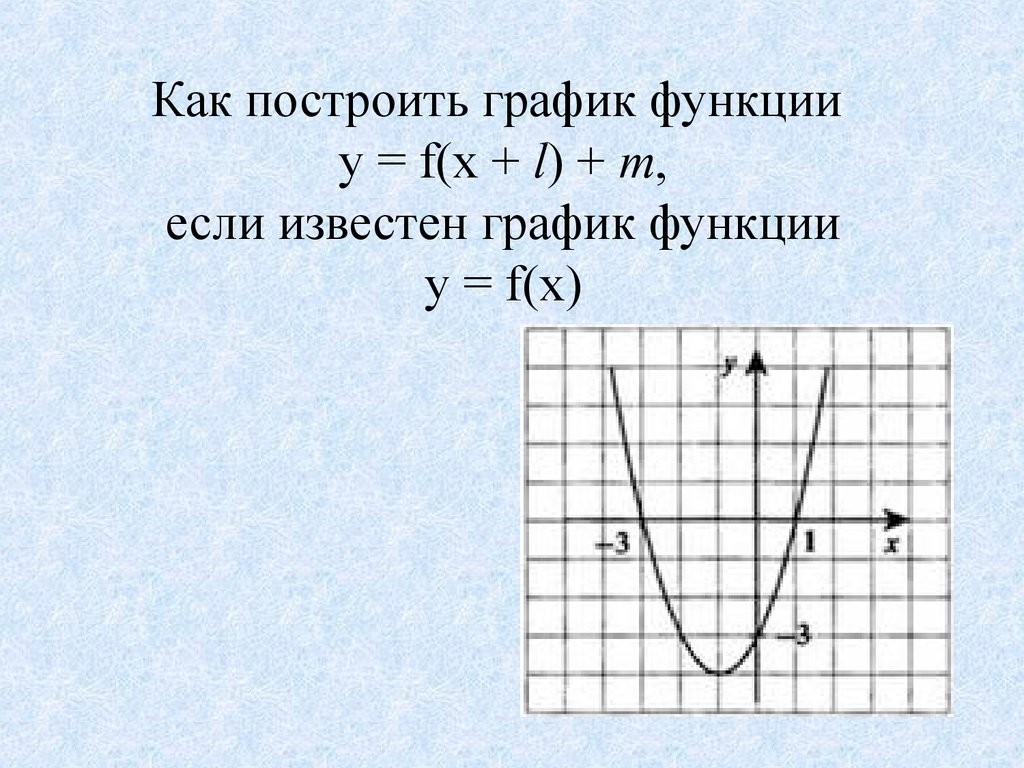
Как построить график функцииy = f(x + l) + m,
если известен график функции
y = f(x)
30.
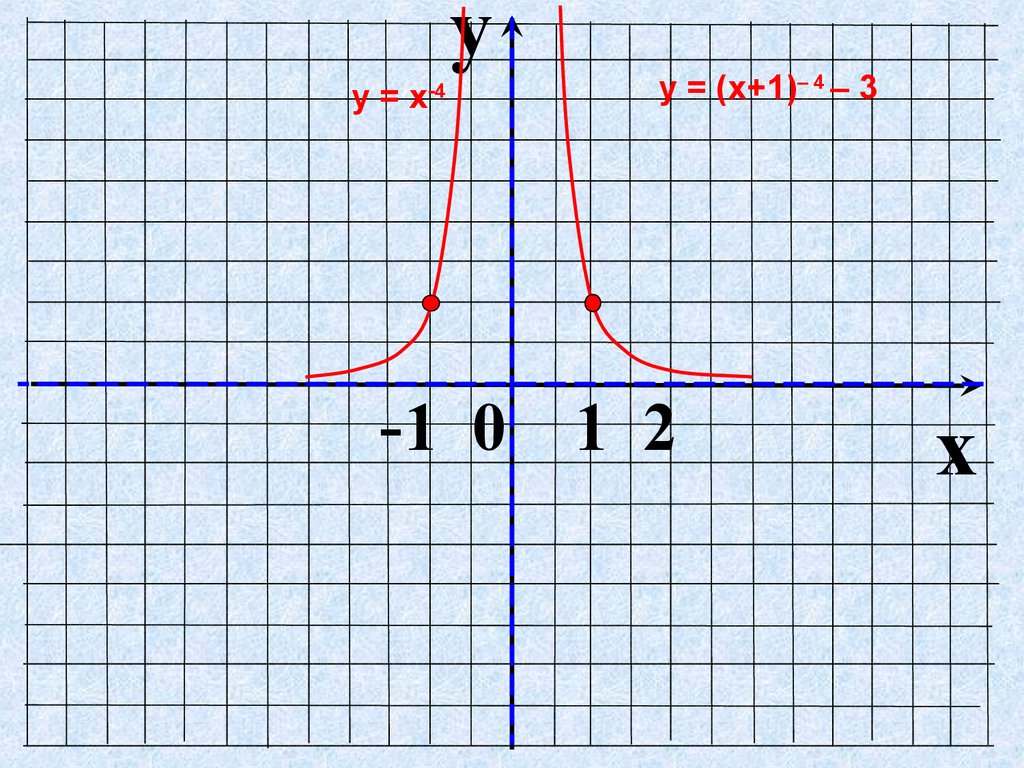
yу = х-4
у = (х+1)– 4 – 3
-1 0 1 2
x
31.
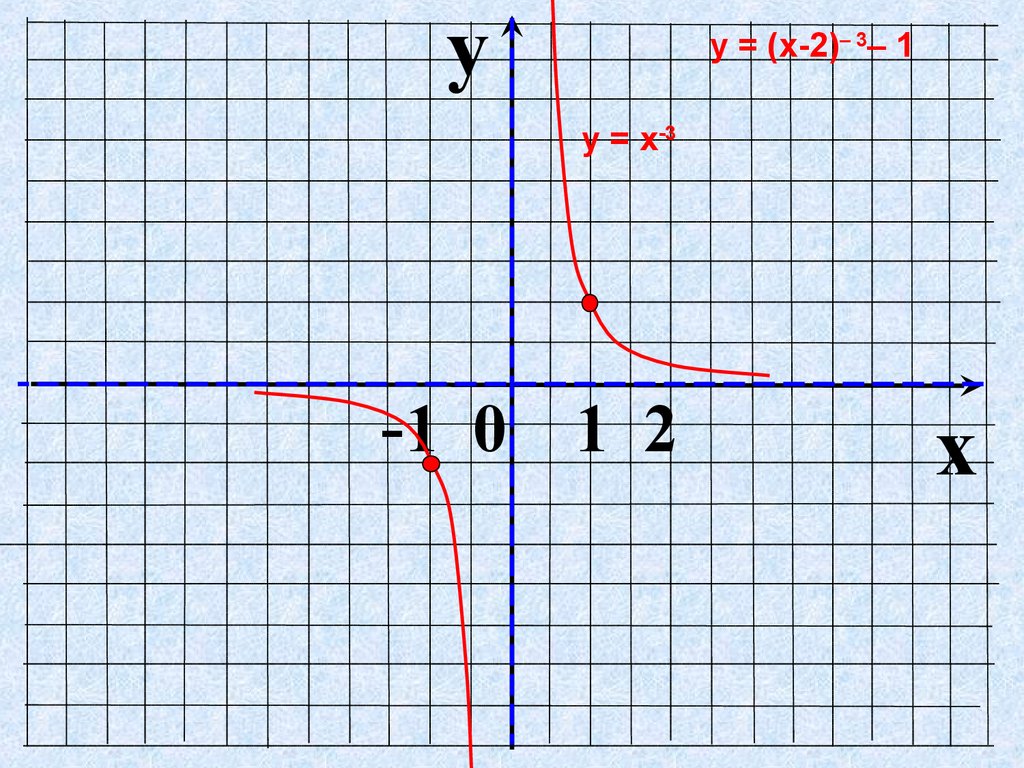
yу = (х-2)– 3– 1
у = х-3
-1 0 1 2
x
32.
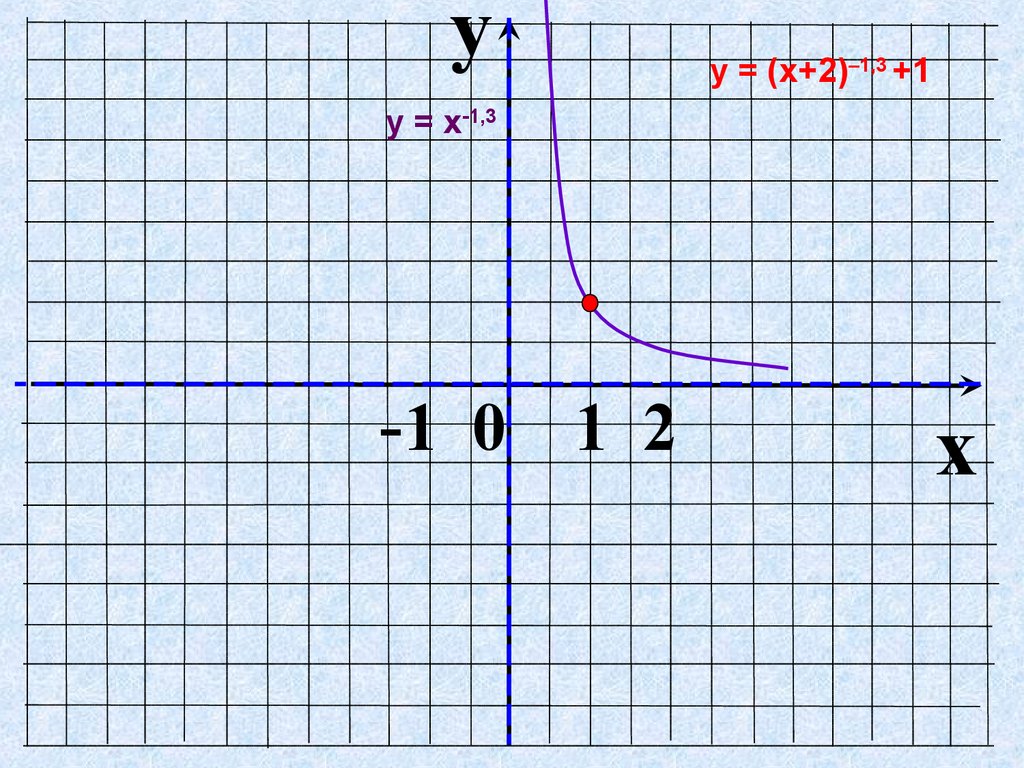
yу = (х+2)–1,3 +1
у = х-1,3
-1 0 1 2
x
33.
Проверим свои знания:Пройдем тестирование,
воспользовавшись ссылкой:
http://anketer.ru/vote/oBDZLxsxTh/
34.
домашнее заданиеп.9, № 9.16(б),
9.19 (а),
9.20 (б),
9.22(в).
п.9, № 9.16(г),
9.19 (б),
9.20 (г),
9.22(г).
35.
видеть график степенной функции по формулеопределять по графику функцию
уметь анализировать график
уметь решать уравнения, неравенства, системы
уравнений с помощью графиков и свойств
степенной функции
развивать навыки мыслительной деятельности,
математической зоркости
умение работать в сообществе
36.
Дружить наукам можно вечно,Вселенная ведь бесконечна.
Спасибо всем вам за урок,
А главное, чтоб он был впрок!
37.
Оцените свою работу на уроке«5»
«4»
«3»
затрудняюсь
Напишите свою фамилию в тот
столбик, на какую оценку, по
Вашему мнению, Вы работали














 Математика
Математика








