Похожие презентации:
Скалярное произведение векторов
1. Скалярное произведение векторов.
2. Цели урока:
Познакомить учащихся с понятием«угол между векторами».
Ввести понятие скалярного
произведения двух векторов,
скалярного квадрата вектора.
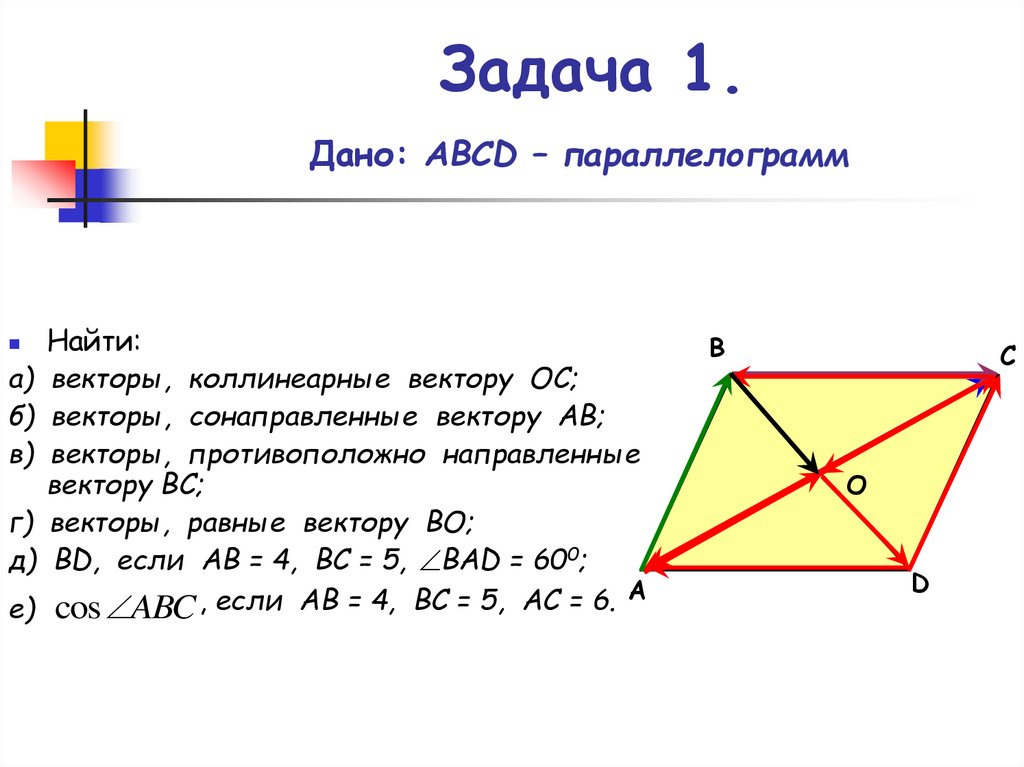
3. Задача 1. Дано: АВСD – параллелограмм
а)б)
в)
г)
д)
е)
Найти:
векторы, коллинеарные вектору ОС;
векторы, сонаправленные вектору АВ;
векторы, противоположно направленные
вектору ВС;
векторы, равные вектору ВО;
ВD, если АВ = 4, ВС = 5, ВАD = 600;
А
cos ABC , если АВ = 4, ВС = 5, АС = 6.
В
С
О
D
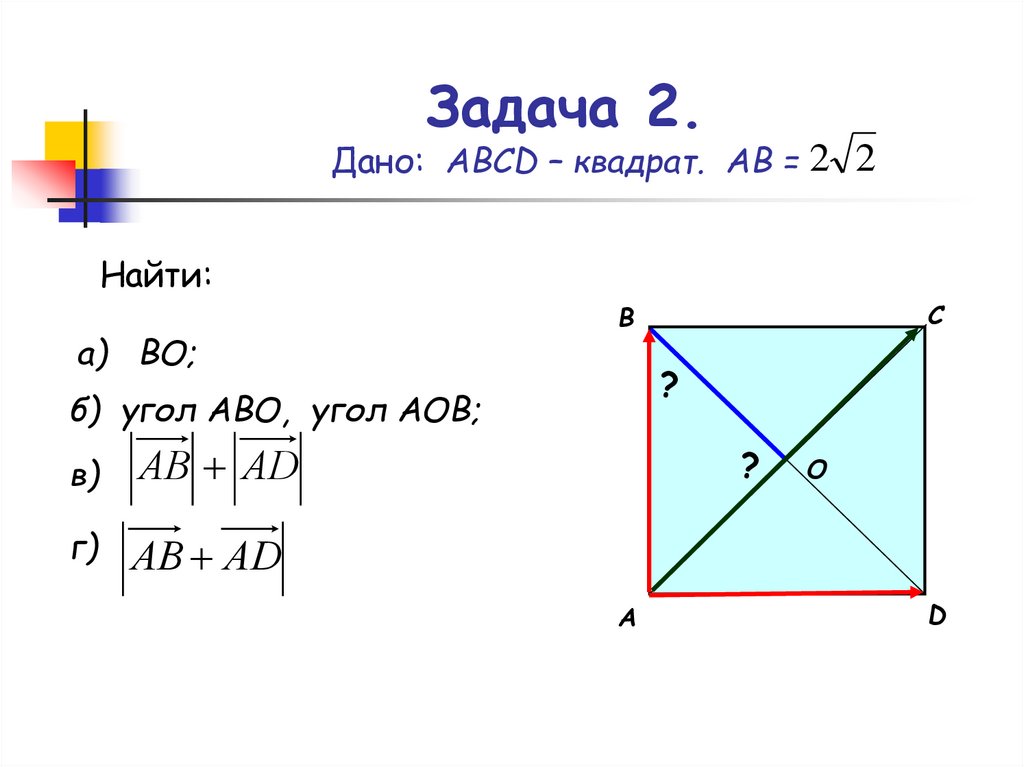
4. Задача 2. Дано: АВСD – квадрат. АВ =
2 2Найти:
а) ВО;
?
б) угол АВО, угол АОВ;
в)
АВ АD
г)
АВ АD
С
В
?
А
O
D
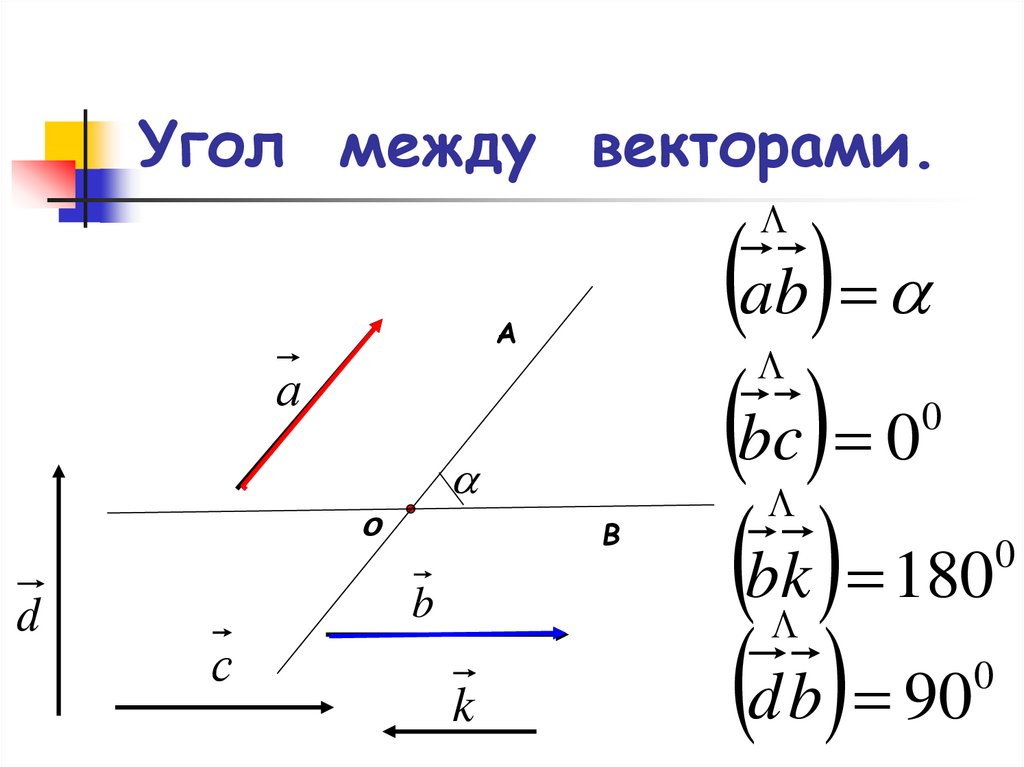
5. Угол между векторами.
abbc 0
bk 180
d b 90
А
а
0
О
d
В
b
с
k
0
0
6. Ответьте на вопросы:
а1. Чему равен угол между
векторами а и b?
2. Каков угол между
векторами b и с?
3. Угол между векторами
c и d?
4. Угол между векторами
с и f острый или тупой?
5. Определите угол между
векторами а f и d.
6. Угол между векторами
а и f?
b
d
О
с
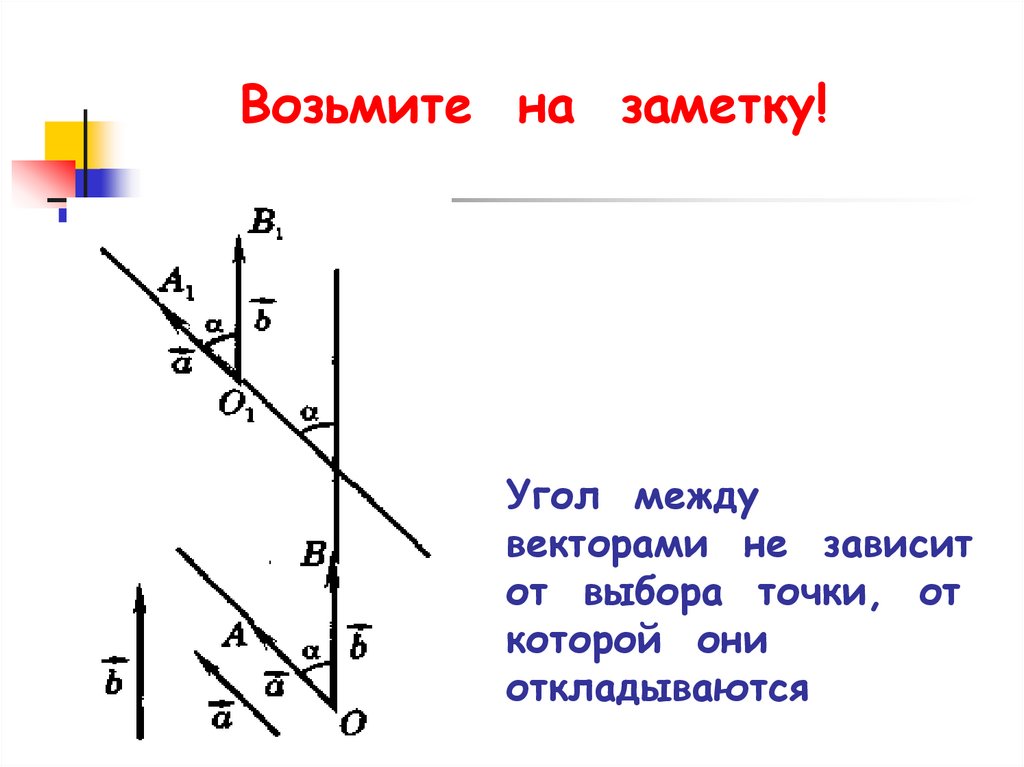
7. Угол между векторами не зависит от выбора точки, от которой они откладываются
Возьмите на заметку!Угол между
векторами не зависит
от выбора точки, от
которой они
откладываются
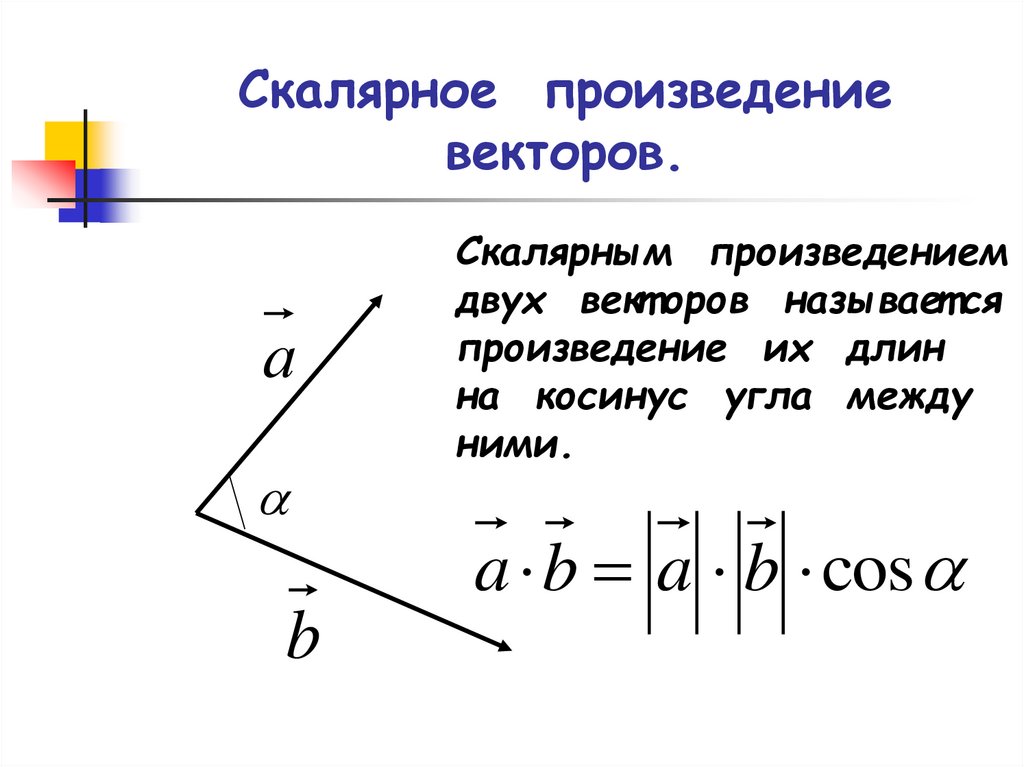
8. Скалярное произведение векторов.
аb
Скалярным произведением
двух вект оров называет ся
произведение их длин
на косинус угла между
ними.
a b a b cos
9.
a b a b cosЕсли
a b, то
a b 0
cos 90 0
0
Если
a b , то cos180 1 a b a b
Если
а b
Если
0
, то cos 0 1
0
a b a b
2
a b , то a b a a a a a a
Скалярное произведение
a a
называется
скалярным квадратом вектора
2
10. Примечание:
В термине«скалярное произведение» первое
слово указывает на то, что
результат действия есть скаляр,
т.е. действительное число. Второе
слово подчеркивает, что для
этого действия имеют силу
основные свойства обычного
умножения.
11. Свойства умножения:
а b b a- переместительное свойство
k a b k a b
a b c ac bc
- сочетательное свойство
- распределительное
свойство
12. Тест:
Вставьте пропущенное слово:Скалярным произведением двух
векторов называется число,
равное произведению модулей
косинус
этих векторов на __________
угла между ними.
13. Вектор а скалярно умножили на вектор b. Как можно охарактеризовать результат этого действия?
1.2.
3.
Результат действия есть вектор.
Результат действия есть скаляр.
Результат действия есть скаляр,
если векторы а и b
коллинеарные, или вектор, если
векторы а и b не являются
коллинеарными.
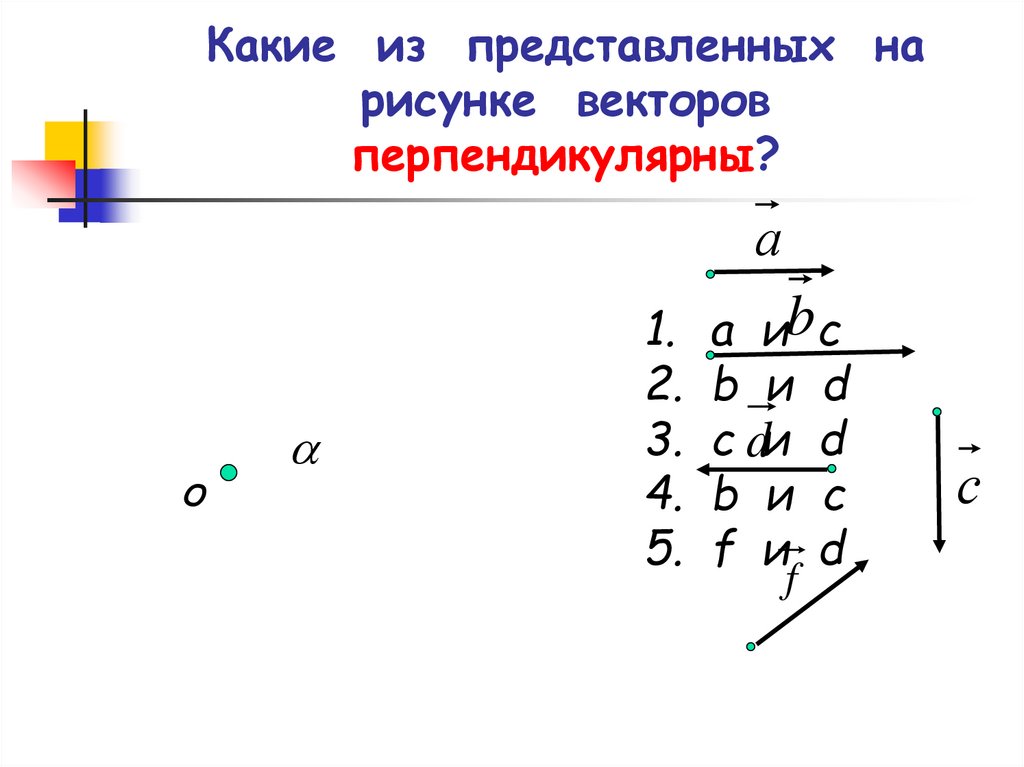
14. Какие из представленных на рисунке векторов перпендикулярны?
аО
1.
2.
3.
4.
5.
а иb c
b и d
с dи d
b и с
f и d
f
с
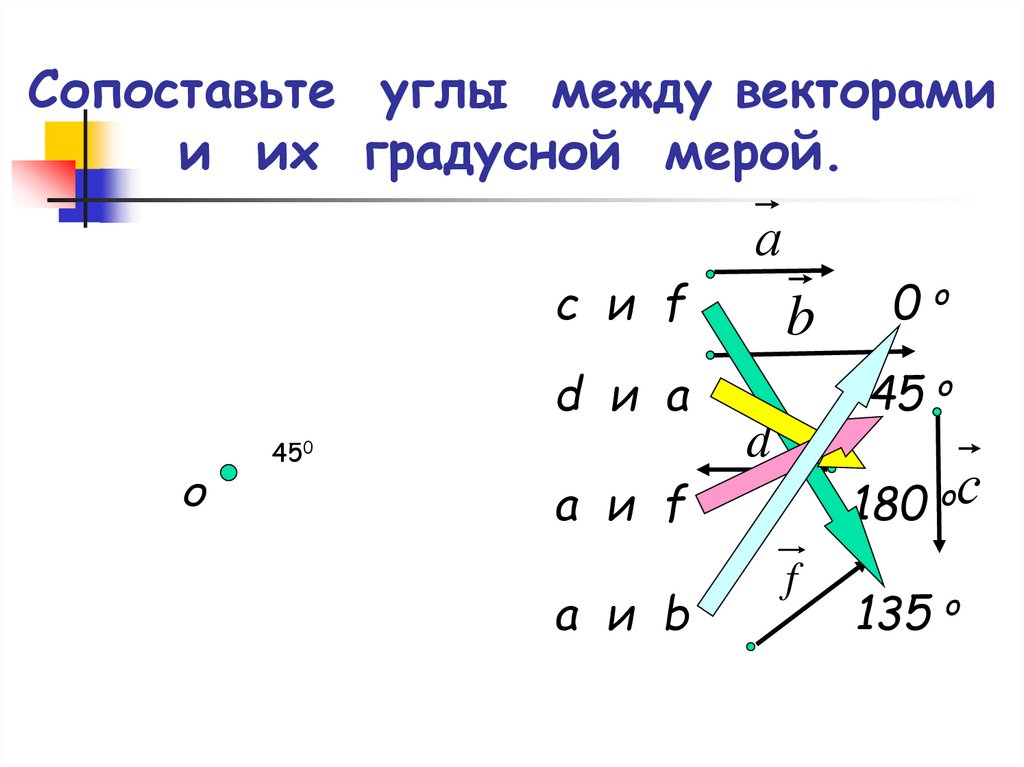
15. Сопоставьте углы между векторами и их градусной мерой.
аc и f
d и a
450
О
b
o
45 o
d
a и f
a и b
0
f
с
180
o
135
o
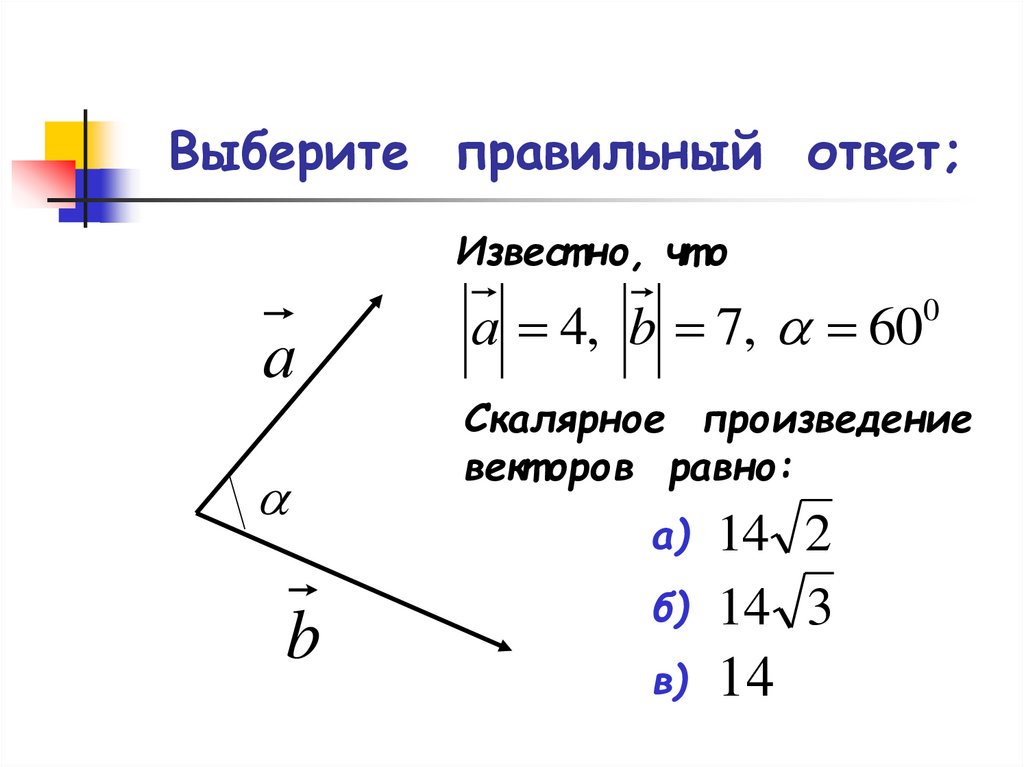
16. Выберите правильный ответ;
Извест но, чт оа
b
а 4, b 7, 60
0
Скалярное произведение
вект оров равно:
а)
б)
14 2
14 3
в)
14
17. Вставьте пропущенное слово:
• Скалярное произведениеаа
называется
скалярным
____________
квадратом вектора
а
квадрат
• Скалярный ___________
вектора равен
квадрату его модуля.









 Математика
Математика








