Скалярное произведение векторов

1. Скалярное произведение векторов

Геометрия 8 класс

2.

Скалярным произведением
векторов
и b b ;b
а а ;а
1
2
1 2
называется (п.98)
число
a b а1b1 a2b2

3. Дано:

Найти: ab, ac, ad,
а (-2;2) aе, dc, ее
b (3;9)
с (0;7)
d (0;0)
е (5;-4)
ав

4. Вывод:

Скалярное
произведение
векторов – число,
а не вектор

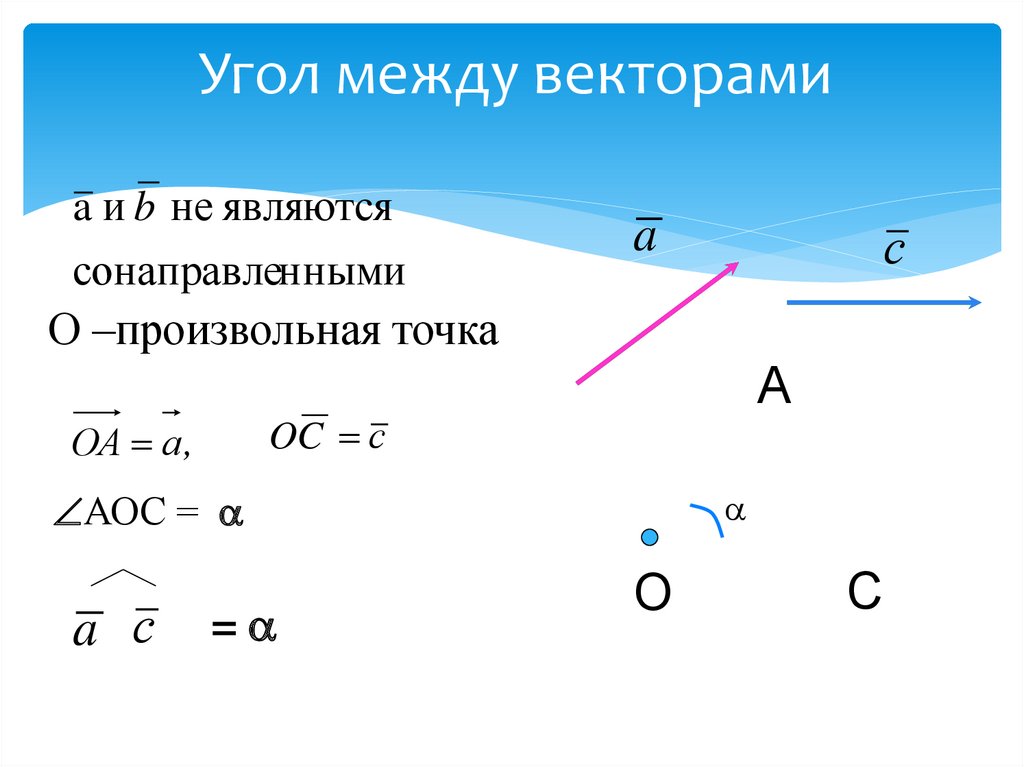
5. Угол между векторами

a и b не являются
сонаправленными
a
с
О –произвольная точка
А
OC с
ОА а ,
АОС =
a с
=
О
С

6.

Угол между векторами
не зависит от выбора
точки,
от которой они
откладываются

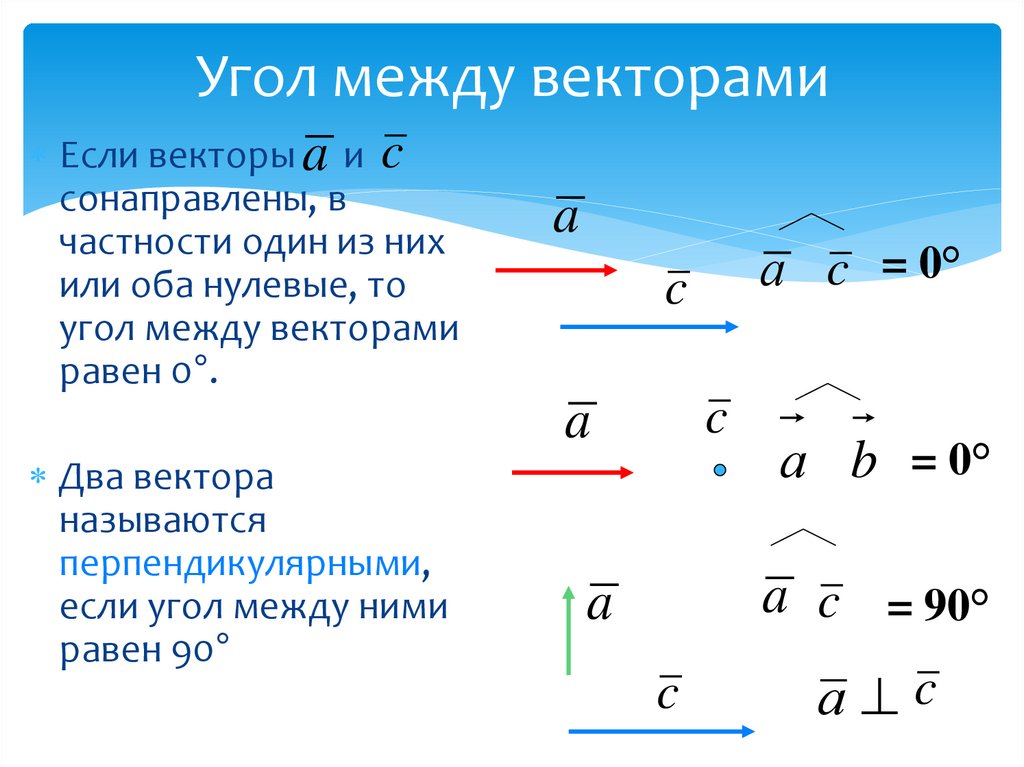
7. Угол между векторами

Если векторы a и c
сонаправлены, в
частности один из них
или оба нулевые, то
угол между векторами
равен 0°.
Два вектора
называются
перпендикулярными,
если угол между ними
равен 90°
a
а c = 0°
c
c
a
а b = 0°
a c = 90°
a
c
а c

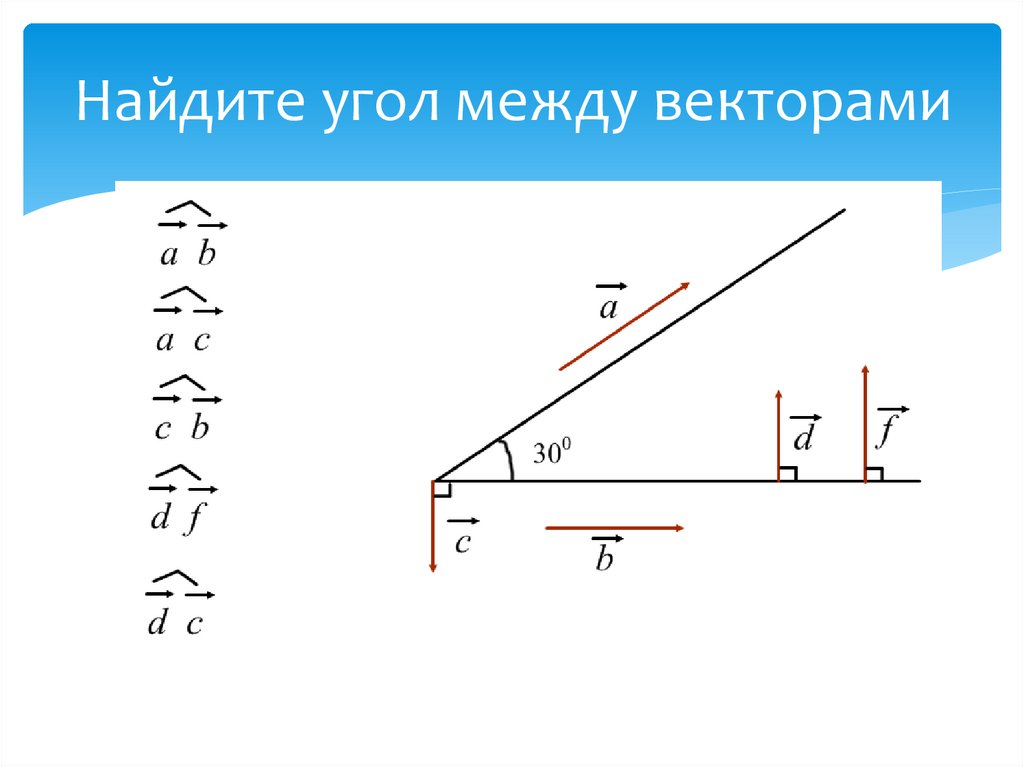
8. Найдите угол между векторами

9. Скалярное произведение векторов (стр.137)

Определение. Скалярное произведение векторов
равно произведению их абсолютных величин
на косинус угла между ними
а b a b cos a b

10. Скалярное произведение векторов

Определение. Скалярным произведением векторов
называется произведение их абсолютных величин
на косинус угла между ними
а b a b cos a b
Пример:
a 5,
b 8,
угол между векторами a и b 45
0
a b a b cos
2
a b 5 8 cos 45 40 cos 45 40
20 2
2
0
0

11. Скалярное произведение векторов

Определение. Скалярным произведением векторов
называется произведение их длин на косинус угла
между ними
а b a b cos a b
Выразить косинус угла:
а в
cos a b
а в

12. Решаем задачу №29

13. Необходимое и достаточное условие равенства нулю скалярного произведения

Скалярное произведение ненулевых векторов
равно нулю
тогда и только тогда
когда эти векторы перпендикулярны
1
a 0
c 0 a c 0
a c
2
a 0
c 0 a c
a c 0

14.

1
a 0
c 0 a c 0
a c
2
а с a с cos a с
а с a с cos 90
cos 90 0
0
a c 0
0
a 0
c 0 a c
a c 0
a c 0
a с cos a с 0
a 0 a 0; c 0 c 0
0
a
c
90
cos a c 0
a c

15. Скалярный квадрат

Скалярным квадратом вектора a
называется
скалярное произведение
a a
a a a a cos a a
cos a a соs 0 1
0
a a a a a
a
a
2
Скалярный квадрат вектора равен квадрату его длины.

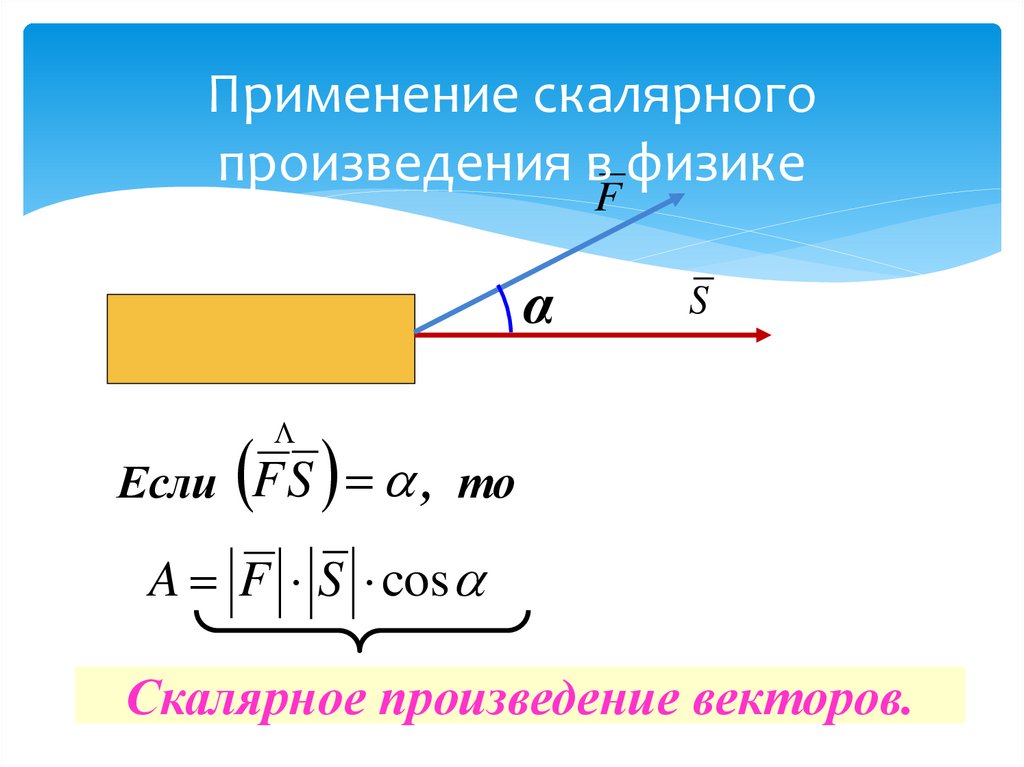
16.

Применение скалярного
произведения в физике
F
α
S
Если F S , то
A F S cos
Скалярное произведение векторов.

17. Самое главное

Скалярным произведением векторов называется
произведение их длин на косинус угла между
ними
Скалярное произведение ненулевых векторов
равно нулю тогда и только тогда когда эти
векторы перпендикулярны
Скалярное произведение вектора самого на себя
называется скалярным квадратом вектора
Скалярный квадрат вектора равен квадрату его
длины.

18. Домашнее задание

П.98 № 32, 35