Похожие презентации:
Thermomechanical action of ultrashort laser pulses on metallic nanostructures
1.
Thermomechanical action of ultrashort laserpulses on metallic nanostructures
Oleg Romanov1, Gennady Romanov2
Belarusian State University, Minsk, Belarus
2 A.V. Luikov Heat and Mass Transfer Institute, National
Academy of Sciences of Belarus, Minsk, Belarus
1
Advances in Nonlinear Photonics
2014 г.
2.
Introduction2
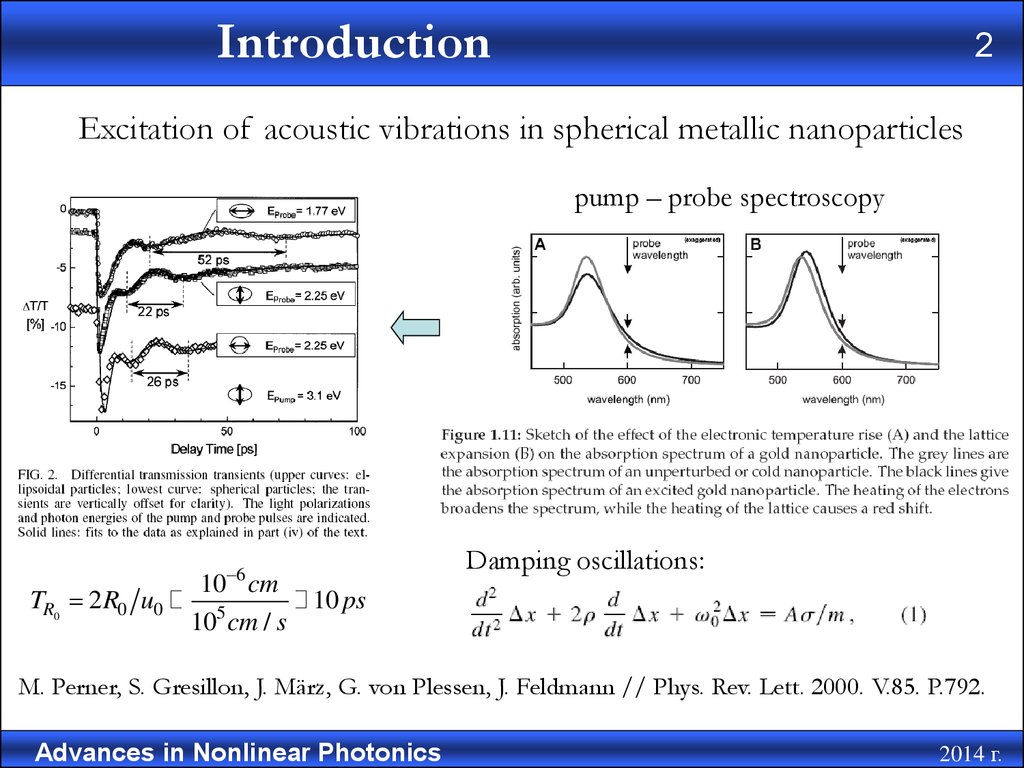
Excitation of acoustic vibrations in spherical metallic nanoparticles
pump – probe spectroscopy
TR0 2 R0 u0
6
10 cm
10 ps
5
10 cm / s
Damping oscillations:
M. Perner, S. Gresillon, J. März, G. von Plessen, J. Feldmann // Phys. Rev. Lett. 2000. V.85. P.792.
Advances in Nonlinear Photonics
2014 г.
3.
Introduction3
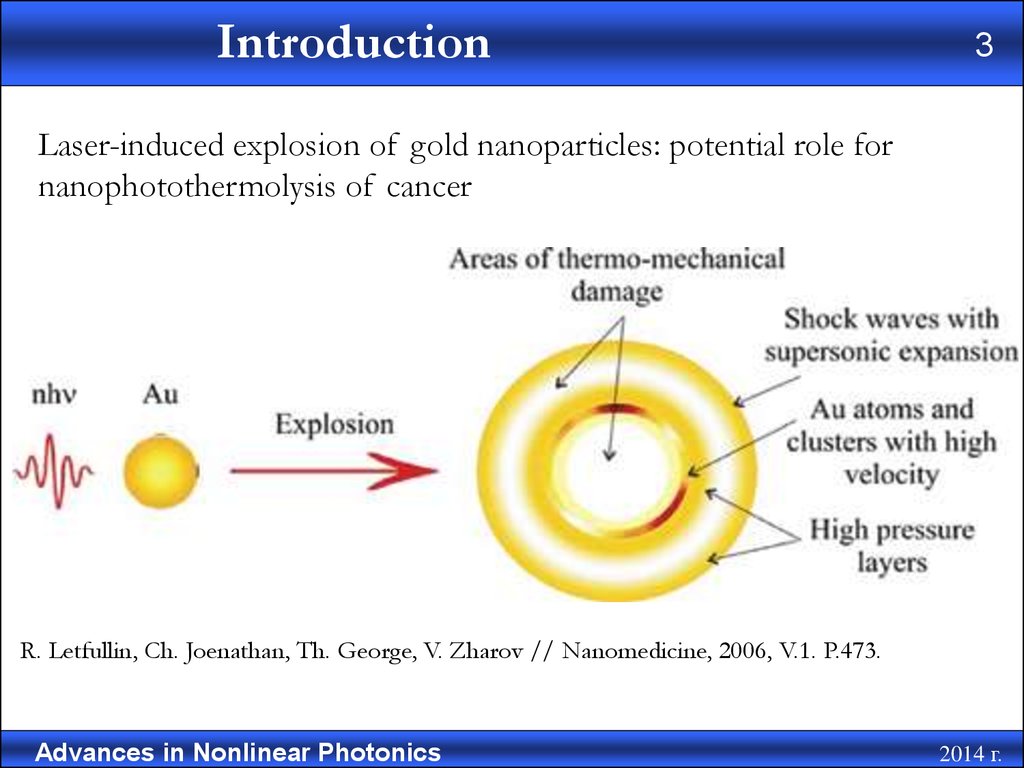
Laser-induced explosion of gold nanoparticles: potential role for
nanophotothermolysis of cancer
R. Letfullin, Ch. Joenathan, Th. George, V. Zharov // Nanomedicine, 2006, V.1. P.473.
Advances in Nonlinear Photonics
2014 г.
4.
Introduction4
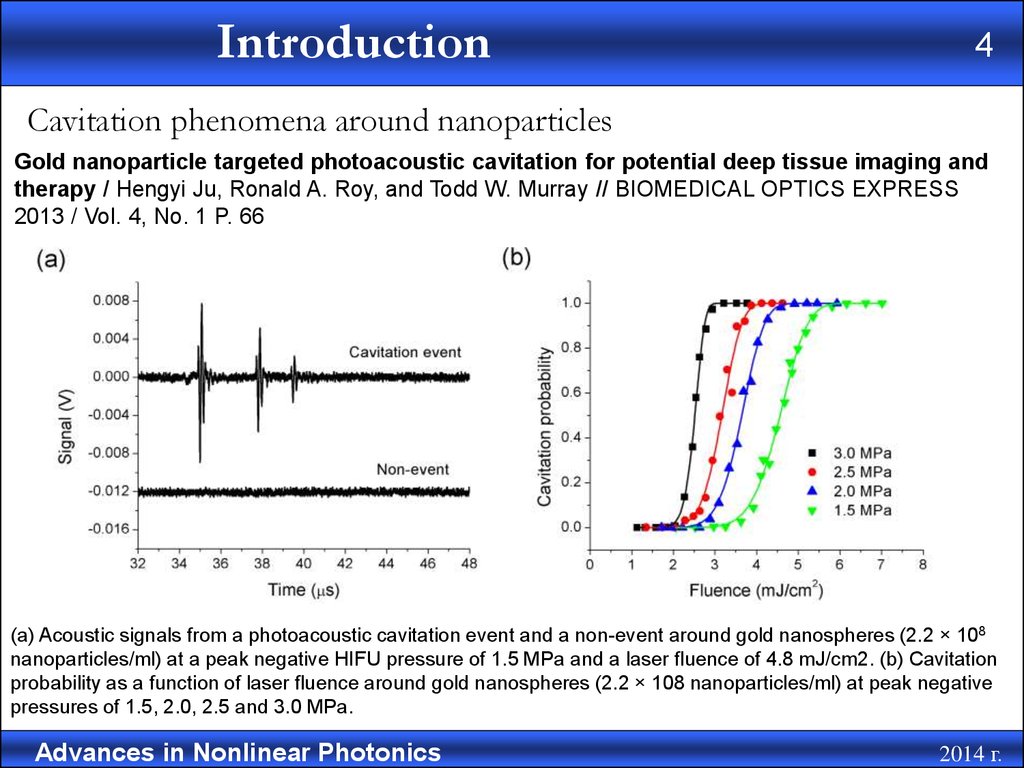
Cavitation phenomena around nanoparticles
Gold nanoparticle targeted photoacoustic cavitation for potential deep tissue imaging and
therapy / Hengyi Ju, Ronald A. Roy, and Todd W. Murray // BIOMEDICAL OPTICS EXPRESS
2013 / Vol. 4, No. 1 P. 66
(a) Acoustic signals from a photoacoustic cavitation event and a non-event around gold nanospheres (2.2 × 108
nanoparticles/ml) at a peak negative HIFU pressure of 1.5 MPa and a laser fluence of 4.8 mJ/cm2. (b) Cavitation
probability as a function of laser fluence around gold nanospheres (2.2 × 108 nanoparticles/ml) at peak negative
pressures of 1.5, 2.0, 2.5 and 3.0 MPa.
Advances in Nonlinear Photonics
2014 г.
5.
Introduction5
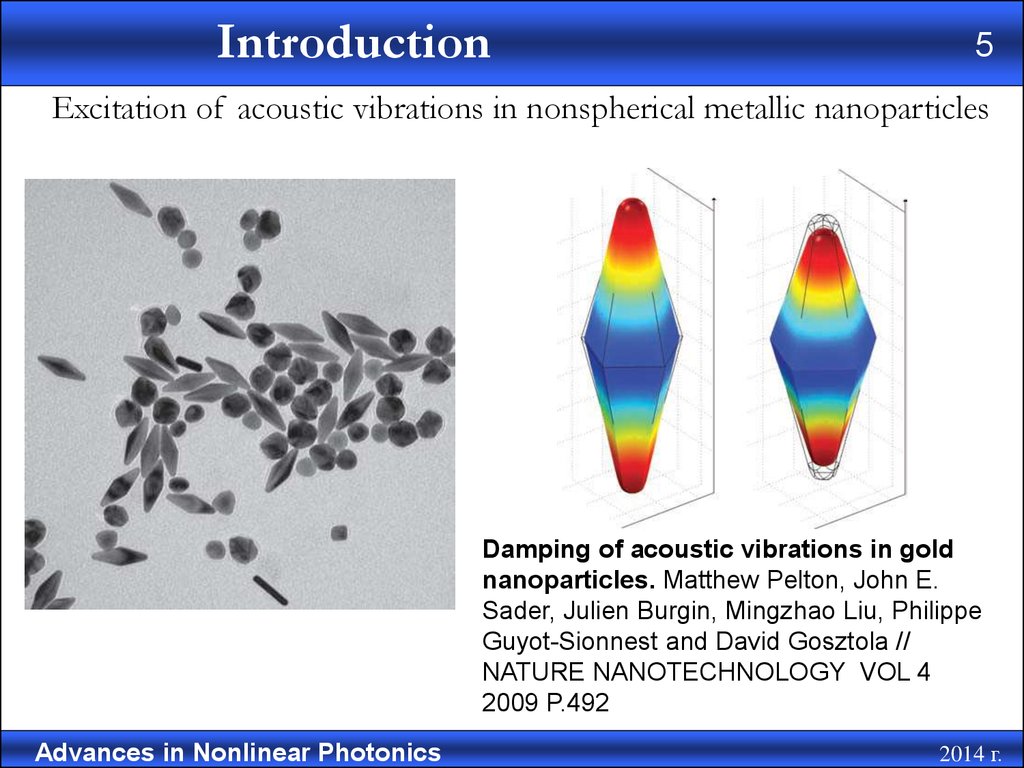
Excitation of acoustic vibrations in nonspherical metallic nanoparticles
Damping of acoustic vibrations in gold
nanoparticles. Matthew Pelton, John E.
Sader, Julien Burgin, Mingzhao Liu, Philippe
Guyot-Sionnest and David Gosztola //
NATURE NANOTECHNOLOGY VOL 4
2009 P.492
Advances in Nonlinear Photonics
2014 г.
6.
Introduction6
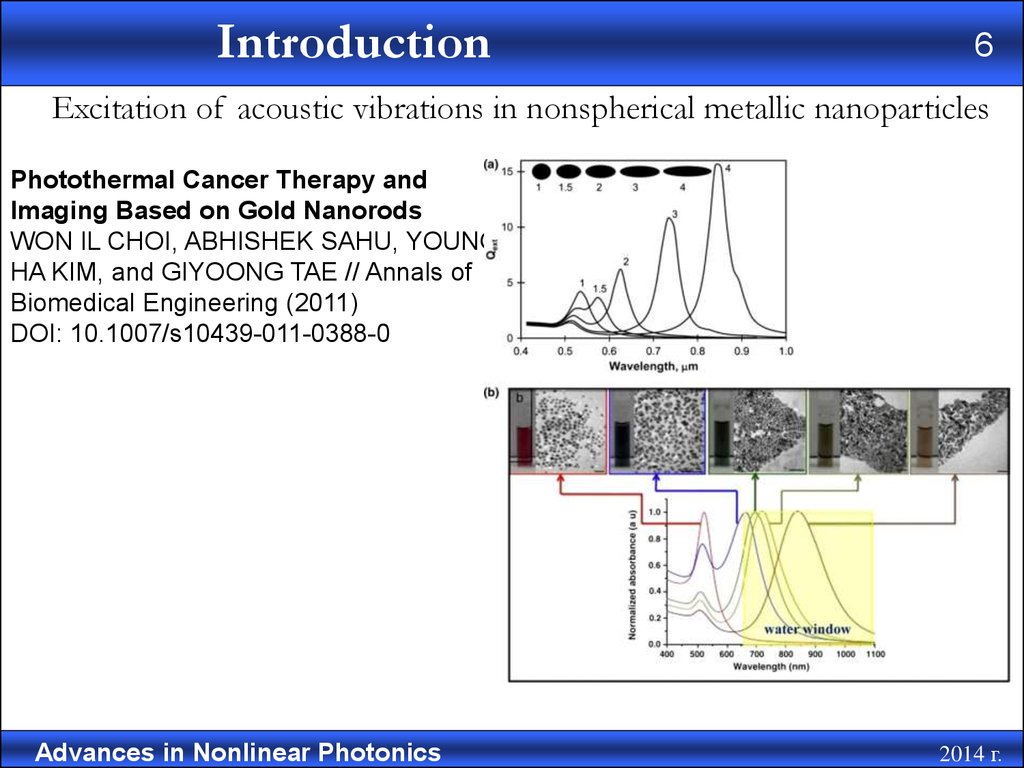
Excitation of acoustic vibrations in nonspherical metallic nanoparticles
Photothermal Cancer Therapy and
Imaging Based on Gold Nanorods
WON IL CHOI, ABHISHEK SAHU, YOUNG
HA KIM, and GIYOONG TAE // Annals of
Biomedical Engineering (2011)
DOI: 10.1007/s10439-011-0388-0
Advances in Nonlinear Photonics
2014 г.
7.
Introduction7
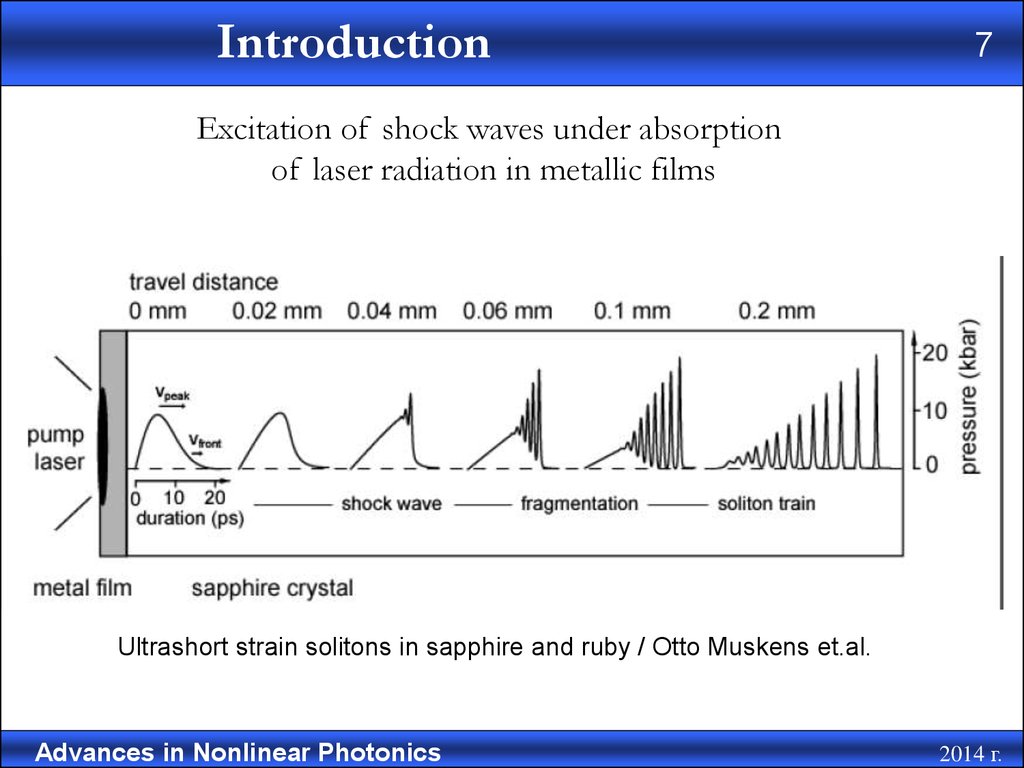
Excitation of shock waves under absorption
of laser radiation in metallic films
Ultrashort strain solitons in sapphire and ruby / Otto Muskens et.al.
Advances in Nonlinear Photonics
2014 г.
8.
Introduction8
Hypersonic Modulation of Light in Three-Dimensional Photonic and Phononic
Band-Gap Materials
A. V. Akimov, Y. Tanaka, A. B. Pevtsov, S. F. Kaplan, V. G. Golubev, S. Tamura, D. R. Yakovlev, and
M. Bayer // Phys. Rev. Lett. 101, 033902
Advances in Nonlinear Photonics
2014 г.
9.
Theoretical model9
Main stages of
thermooptical excitation of
acoustic pulse:
r
I0
External
medium
R0
Small particle
Advances in Nonlinear Photonics
-absorption of laser pulse
energy;
-local heating;
-local pressure increasing;
-expansion due to gradient
of pressure;
-formation of acoustic
pulse;
-relaxation process.
2014 г.
10.
Theoretical model10
The Lagrange equations for the one-dimensional motion of a continuous
medium have the following form [1]:
R
V V0
r
1
R
r
– continuity equation
1
=1 – plane
=2 – cylindrical
=3 – spherical geometry
u
R P – motion equation
V0
t
r r
R
u – equation of the changing of Euler coordinate R
t
C T T0 – Mie–Grünheisen
V
P 0c02 1
V
state equation
V0
C
P (r,t),
u (r,t),
(r,t)
T (r,t)
T
k T Qs – heat transfer equation
t
[1] O.G. Romanov, G.I. Zheltov, G.S. Romanov. Numerical modeling of thermomechanical
processes in absorption of laser radiation in spatially inhomogeneous media // Journal of
Engineering Physics and Thermophysics, 2011. Vol. 84, No. 4, P.772-780.
Advances in Nonlinear Photonics
2014 г.
11.
Theoretical model11
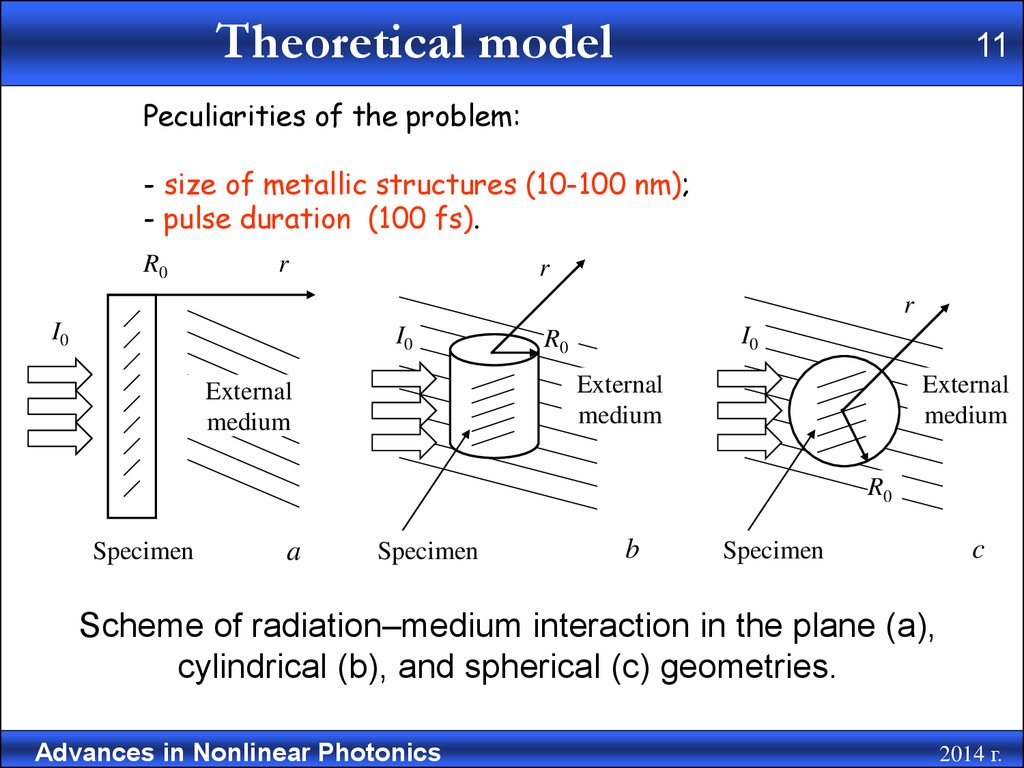
Peculiarities of the problem:
- size of metallic structures (10-100 nm);
- pulse duration (100 fs).
R0
r
r
r
I0
I0
I0
R0
External
medium
External
medium
External
medium
R0
Specimen
a
Specimen
b
Specimen
c
Scheme of radiation–medium interaction in the plane (a),
cylindrical (b), and spherical (c) geometries.
Advances in Nonlinear Photonics
2014 г.
12.
Theoretical model- particle size (10-100nm);
- pulse duration (100fs);
r
I0
12
External
medium
R0
Fast dynamics in small area
Nanoparticle
Advances in Nonlinear Photonics
2014 г.
13.
Theoretical model13
The heating of metals with ultra short laser pulses is described by a
two-temperature model for an electron gas and an ionic lattice:
heat source function
Te
e 1 2 Te
eCe
kT 2 r
QS Te Ti
t
r r r
Ti
iCi
Te Ti
t
electron-phonon relaxation
S.I.Anisimov, Ya.A. Imas, G.S. Romanov, and Yu.V. Khodyko.
The Effect of High Power Radiation onto Metals, 1970 (in Russian).
Advances in Nonlinear Photonics
2014 г.
14.
Theoretical model14
Mie–Grünheisen state equation for metallic nanoparticle:
P
2
i 0u0 1
Ci Ti T0
Ce Te T0
Vi
e
i
Vi 0
Vi
Ve
Mie–Grünheisen state equation for environment:
P
2
0ul 1
C T T0
V
V0
V
Advances in Nonlinear Photonics
2014 г.
15.
Numerical modelLagrange equations [2]:
V jn 1/1 2
V0
u nj 1 u nj
t
R nj 1 R nj
t
n 1
R j 1
rj 1 rj
V0
p nj q nj R nj
u nj 1
r
rj
q nj 1/ 2
r rj 1 rj
p
Pjn 1/ 2
1
Artificial viscosity
t t n 1 t n
n
j
[2] R.D. Richtmayer, and K.W.
Morton, Difference Methods for
Initial Value Problems, 1967.
n 1
Rj
15
Pjn 1/ 2
Advances in Nonlinear Photonics
q nj qnj 1/ 2 q nj 1/ 2
2
2a 2
n
n
u
,
u
0;
n
j 1/ 2
j 1/ 2
n 1
V j 1/ 2 V j 1/ 2
n
0,
u
0;
j 1/ 2
u nj 1/ 2 u nj 1 u nj
2014 г.
16.
Numerical model16
Heat transfer equation [3]:
T jn 1 T jn 1
2 t
1 T jn 1 T jn 1 T jn 1 2T jn T jn 1 V jn
n
kT
Q
S j.
2
CV
CV rj
2 r
r
V jn
T jn 12 T jn 1 T jn 1
[3] V.K. Saul’ev, Parabolic Equations Integration by Grid Method, 1960
(in Russian).
Advances in Nonlinear Photonics
2014 г.
17.
Results and discussionPlane geometry
α=1
T, K
17
u, см/с
a
1
3 4
5
2
10
6
b
1
0
7
1
7'
0.1
7''
2'
1''
1'
0.01
1E-3
0
5
10
2''
15
-10
нм
20 r,
P, бар
60
I 0 10 W / cm
10
p 100 fs
R0
10nm
105 cm 1
2
-5
1
1
6
c
1.0
0.5
20
0.0
0
-0.5
-20
-1.0
-60
0
6
-15
0
5
10
15
20
r, нм
P, бар
7
40
-40
3 4
2
1
3
4
5
d
6
7
-1.5
2
2
5
4
3
4
6
8
r, нм
-2.0
-2.5
10
15
20
r, нм
Space distributions of temperature (а), velocity (b) and pressure (c, d) in different time moments.
1 – 100 fs, 2 – 500 fs, 3 – 1 ps, 4 – 2 ps, 5 – 3 ps, 6 – 4 ps, 7 – 5 ps
Advances in Nonlinear Photonics
2014 г.
18.
Results and discussionCylindrical geometry
α=2
T, K
7''
1''
2'
p 100 fs
R0
5
10
20 r,
15
c
20
-2
0
нм
5
10
15
20
P, бар
3
1
3
r, нм
d
2
0.50
1
4
4 5
6
7
0.25
2
0
0.00
10nm
105 cm 1
0
6
P, бар
I 0 10 W / cm
б
2''
1'
1E-3
0
6
4
7'
0.01
3 4
1
7
0.1
2
2
2
1
10
u, см/с
a
1
10
18
6
5
-20
0
2
7
4
6
8
-0.25
10
r, нм
15
20
r, нм
Space distributions of temperature (а), velocity (b) and pressure (c, d) in different time moments.
1 – 100 fs, 2 – 500 fs, 3 – 1 ps, 4 – 2 ps, 5 – 3 ps, 6 – 4 ps, 7 – 5 ps
Advances in Nonlinear Photonics
2014 г.
19.
Results and discussion19
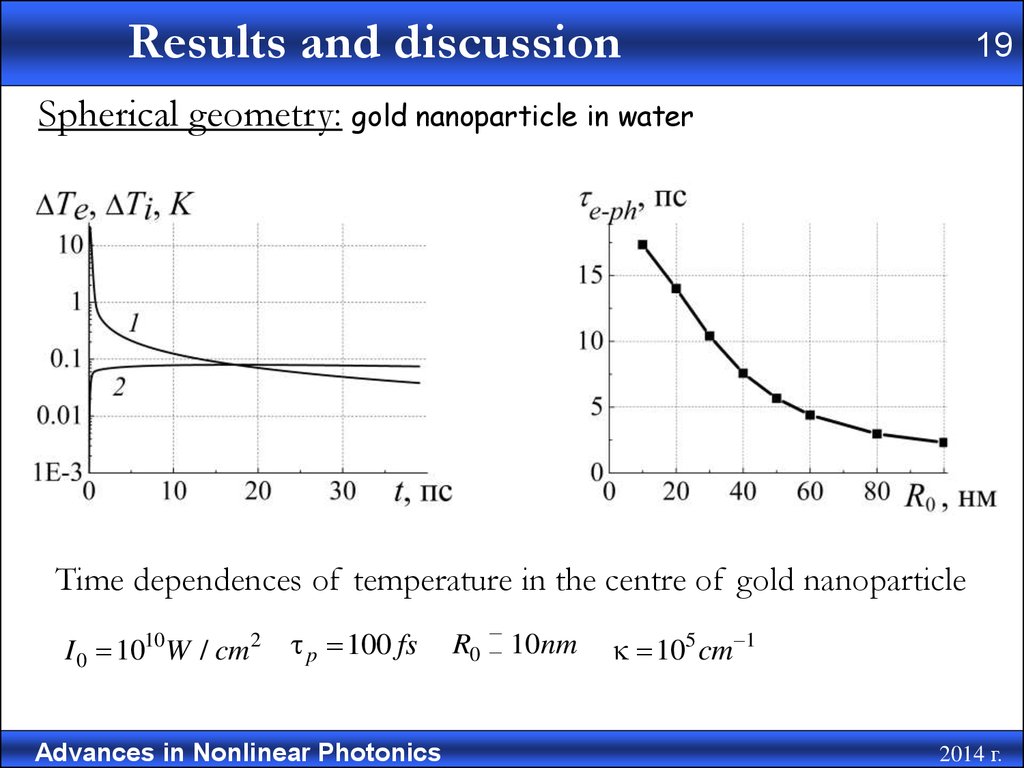
Spherical geometry: gold nanoparticle in water
Time dependences of temperature in the centre of gold nanoparticle
I 0 1010W / cm 2 p 100 fs
Advances in Nonlinear Photonics
R0
10nm
105 cm 1
2014 г.
20.
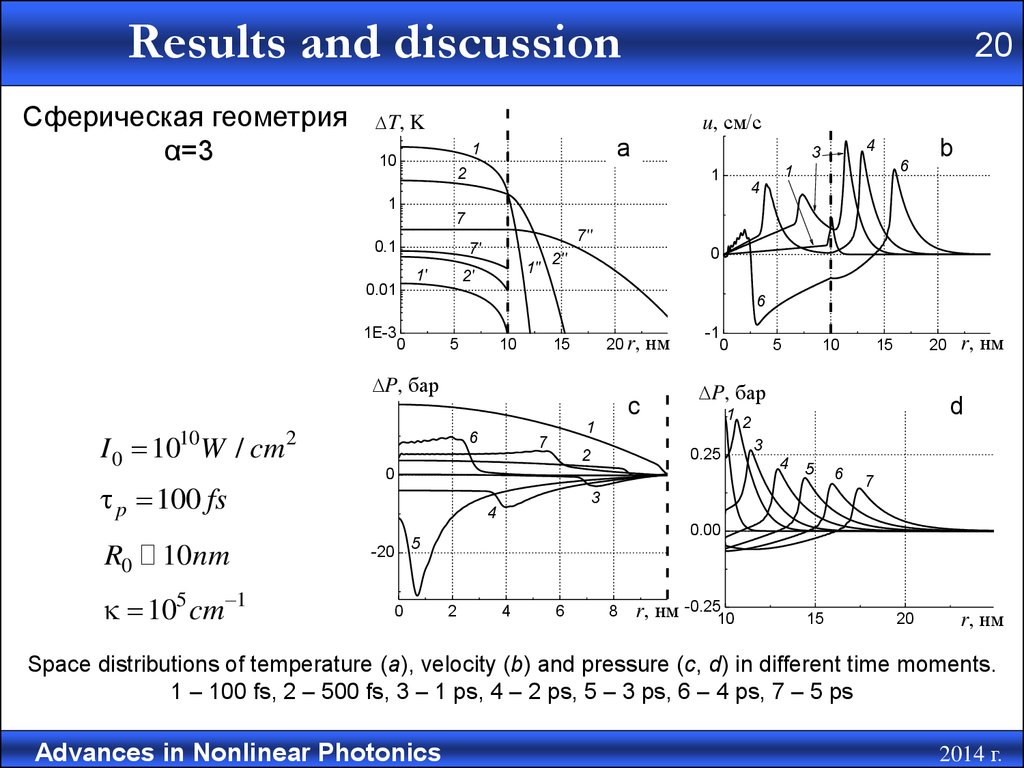
Results and discussionСферическая геометрия
α=3
20
T, K
u, см/с
a
1
10
4
3
2
6
1
1
b
4
1
7
0.1
0.01
7''
7'
1'
1''
2'
0
2''
6
1E-3
0
5
10
20 r,
15
P, бар
I 0 10 W / cm
10
p 100 fs
R0
10nm
105 cm 1
c
2
нм
-1
0
7
1
0.25
2
10
15
20
P, бар
1
6
5
0
r, нм
d
2
3
4
5
6
7
3
4
-20
0.00
5
0
2
4
6
8
r, нм -0.2510
15
20
r, нм
Space distributions of temperature (а), velocity (b) and pressure (c, d) in different time moments.
1 – 100 fs, 2 – 500 fs, 3 – 1 ps, 4 – 2 ps, 5 – 3 ps, 6 – 4 ps, 7 – 5 ps
Advances in Nonlinear Photonics
2014 г.
21.
Results and discussion21
Spherical geometry: gold nanoparticle in water
R/R0
-7
6.0x10
-7
4.0x10
-7
2.0x10
0.0
-7
-2.0x10
0
10
20
30
t, ps
TR0 2 R0 u0 6.2 ps
Oscillations of nanoparticle
Advances in Nonlinear Photonics
2014 г.
22.
Results and discussion22
Spherical geometry: gold nanoparticle in water
P, bar
P, mbar
6
0.3
4
0.2
2
0.1
0
0.0
-2
-0.1
0
10
20
30
40
tp=10-13s, I0=1010 W/cm2
t, ps
-4
0
10
20
30
40
t, ps
tp=10-11s, I0=108 W/cm2
Pressure oscillations outside the particle (r =1nm from surface).
Advances in Nonlinear Photonics
2014 г.
23.
Results and discussion23
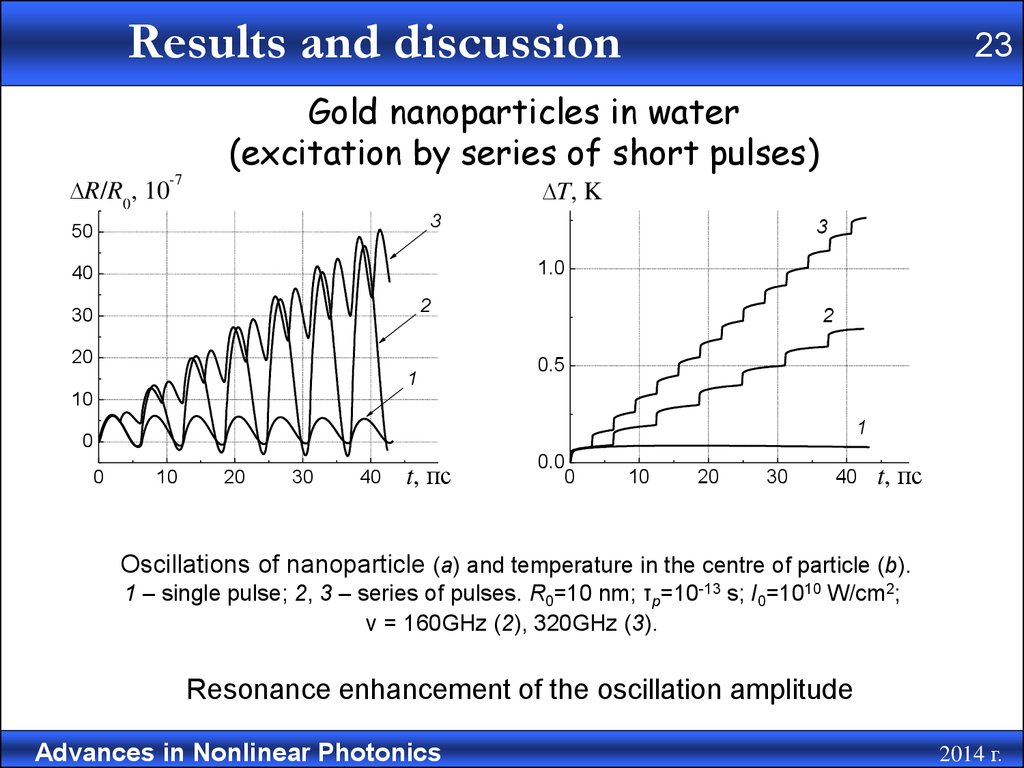
Gold nanoparticles in water
(excitation by series of short pulses)
R/R0, 10
-7
T, K
3
50
3
1.0
40
2
30
20
1
2
0.5
10
1
0
0
10
20
30
40
t, пс
0.0
0
10
20
30
40
t, пс
Oscillations of nanoparticle (а) and temperature in the centre of particle (b).
1 – single pulse; 2, 3 – series of pulses. R0=10 nm; τp=10-13 s; I0=1010 W/cm2;
ν = 160GHz (2), 320GHz (3).
Resonance enhancement of the oscillation amplitude
Advances in Nonlinear Photonics
2014 г.
24.
Results and discussion24
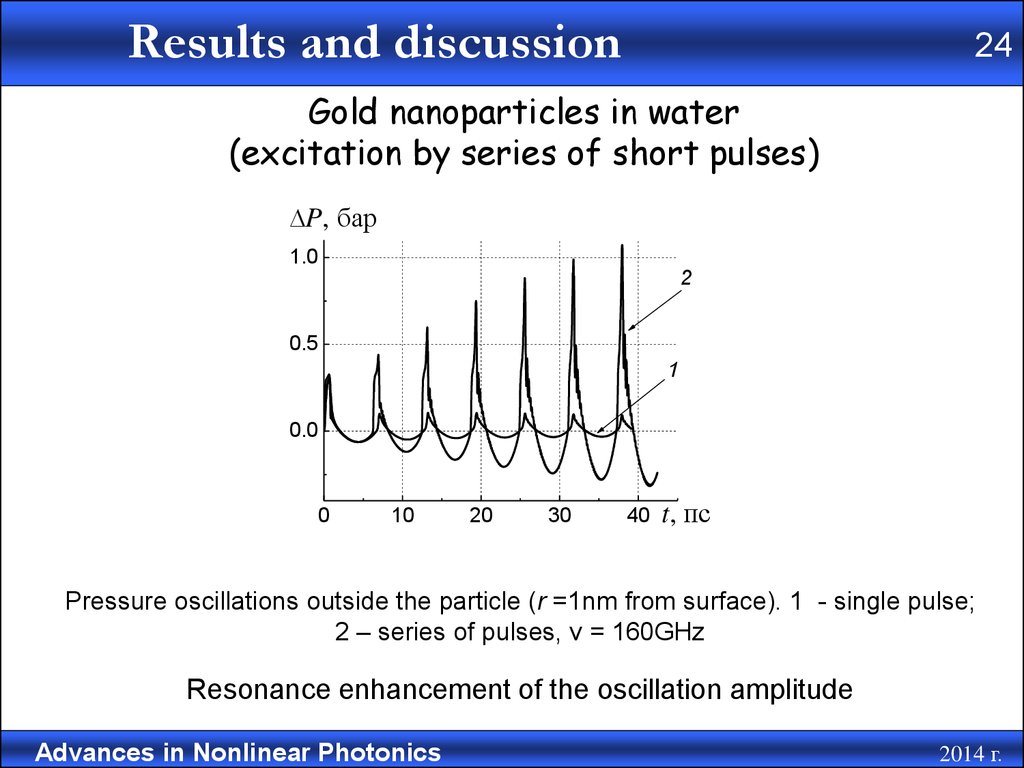
Gold nanoparticles in water
(excitation by series of short pulses)
P, бар
1.0
2
0.5
1
0.0
0
10
20
30
40
t, пс
Pressure oscillations outside the particle (r =1nm from surface). 1 - single pulse;
2 – series of pulses, ν = 160GHz
Resonance enhancement of the oscillation amplitude
Advances in Nonlinear Photonics
2014 г.
25.
Conclusions25
The theoretical model for thermomechanical action of
ultrashort laser pulses on one-dimensional metallic
nanostructures has been developed.
Heating of metals is described based on two-temperature
model for an electronic gas and ionic lattice. Space-time
dynamics of excitation and propagation of acoustic vibrations
inside nanostructures and in a surrounding medium is
investigated based on numerical solution of the equations for a
continuous medium’s motion in the Lagrange form.
Advances in Nonlinear Photonics
2014 г.














 Физика
Физика








