Первообразная

1.

Первообразная.

2.

В математике часто приходиться решать так
называемые обратные задачи. Например, зная
производную фукции, можем восстановить ее
первичный образ.
Восстановленная функция – первообразная
( первичный образ функции)

3.

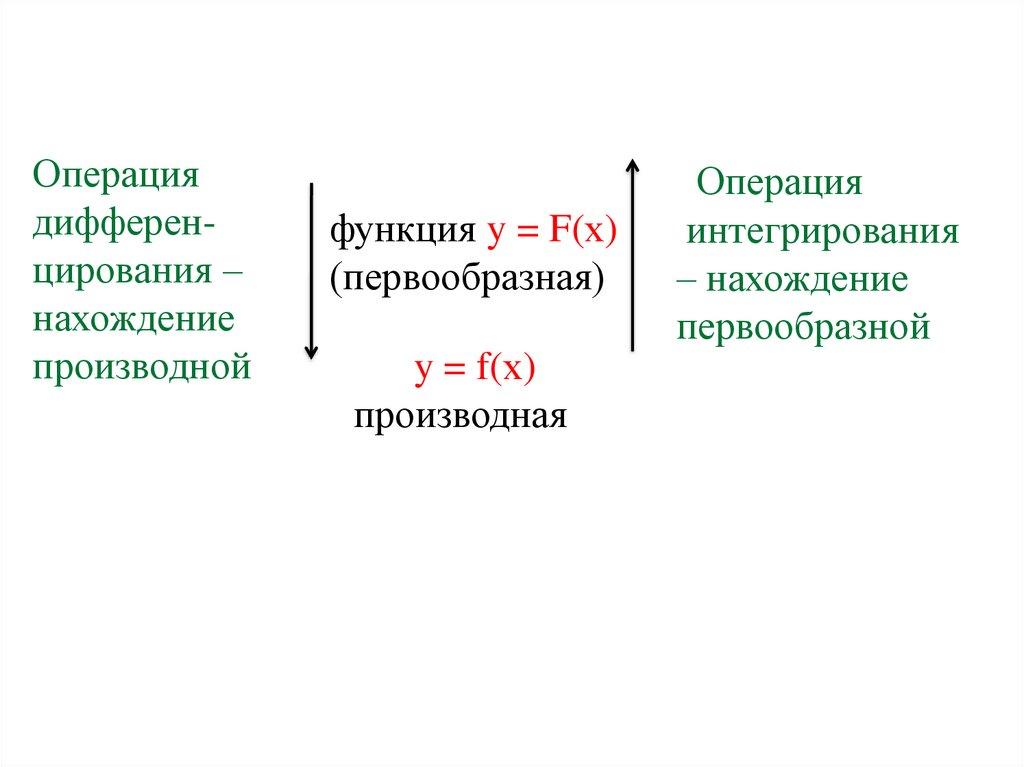
Операция
дифференцирования –
нахождение
производной
функция y = F(х)
(первообразная)
y = f(х)
производная
Операция
интегрирования
– нахождение
первообразной

4.

Функция F(x)называется первообразной
для функции f(x)на некотором промежутке,
если для всех x из этого промежутка
F ( x) f ( x)

5.

Запомните: Первообразная – это родитель
производной:

6.

Если F(x)– первообразная для функции
f(x) на некотором промежутке, то
функция F(x)+C также является
первообразной функции f(x) на этом
промежутке, где C –произвольная
постоянная

7.

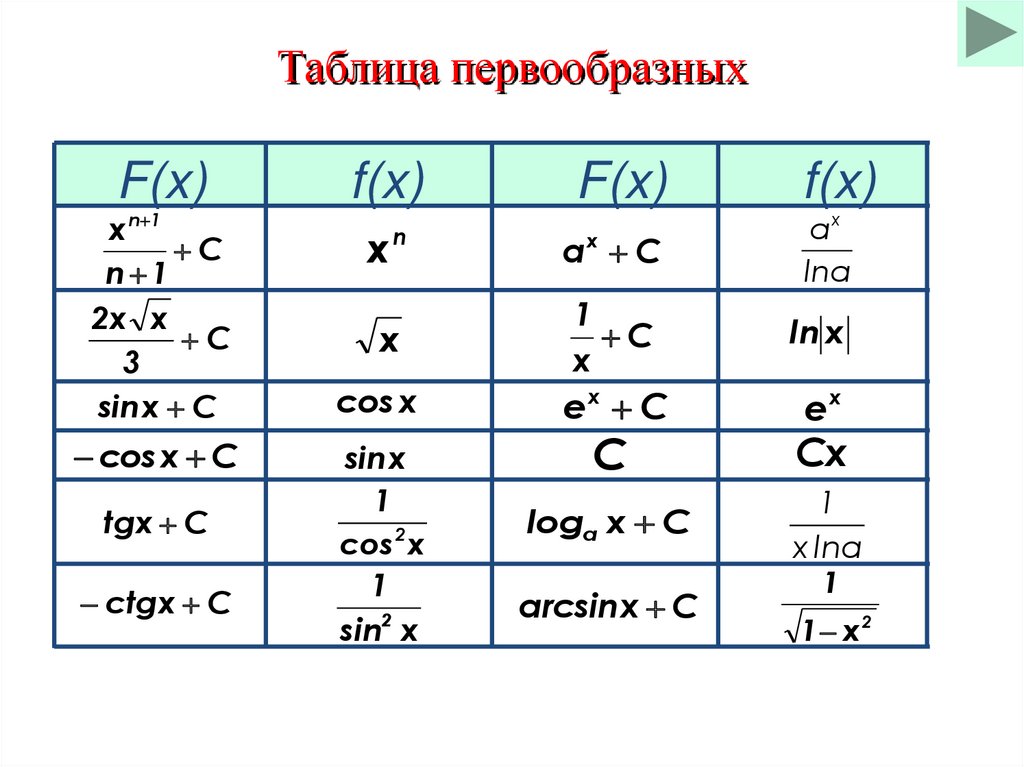
Таблица первообразных
F(x)
x n 1
C
n 1
2x x
C
3
sin x C
cos x C
tgx C
ctgx C
f(x)
f(x)
F(x)
xn
ax C
ax
lna
х
1
C
x
ln x
ex C
ex
cos x
sin x
1
сos 2 x
1
sin2 x
C
Cx
loga x C
1
x lna
arcsin x C
1
1 x2

8.

Правила нахождения
первообразных

9.

Если F(x)– первообразная для функции f(x),
а G(x)– первообразная для функции g(x), то
F(x)+G(x)– первообразная для функции
f(x)+g(x)
Первообразная суммы равна сумме
первообразных

10.

Если F(x)– первообразная для функции f(x),
а а –константа, то аF(x)– первообразная
для функции аf(x)
Постоянный множитель можно
выносить за знак первообразной

11.

Если F(x) – первообразная для функции f(x),
а k и b- константы, причем
k 0
то
1
F (kx b) -первообразная для
функции
k
f (kx b)

12.

5
Показать, что функция
x
F ( x) 1
5
является первообразной для функции
f ( x) x
4
Решение:
5
4
x
5x
4
F ( x) 1
x f ( x)
5
5

13.

F ( x) 1 sin 2 x
Показать, что функция
является первообразной для функции
f ( x) 2 cos 2 x
Решение:
F ( x) 1 sin 2 x 2 cos 2 x f ( x)

14.

Найти первообразные для функции
f ( x) 5 x e
3
2 x 7
4 cos x
Решение:
4
x 1 2 x 7
F ( x) 5 e
4 sin x C
4 2