Похожие презентации:
Определение арктангенса и арккотангенса числа а
1.
Определениеарктангенса и
арккотангенса
числа а
2.
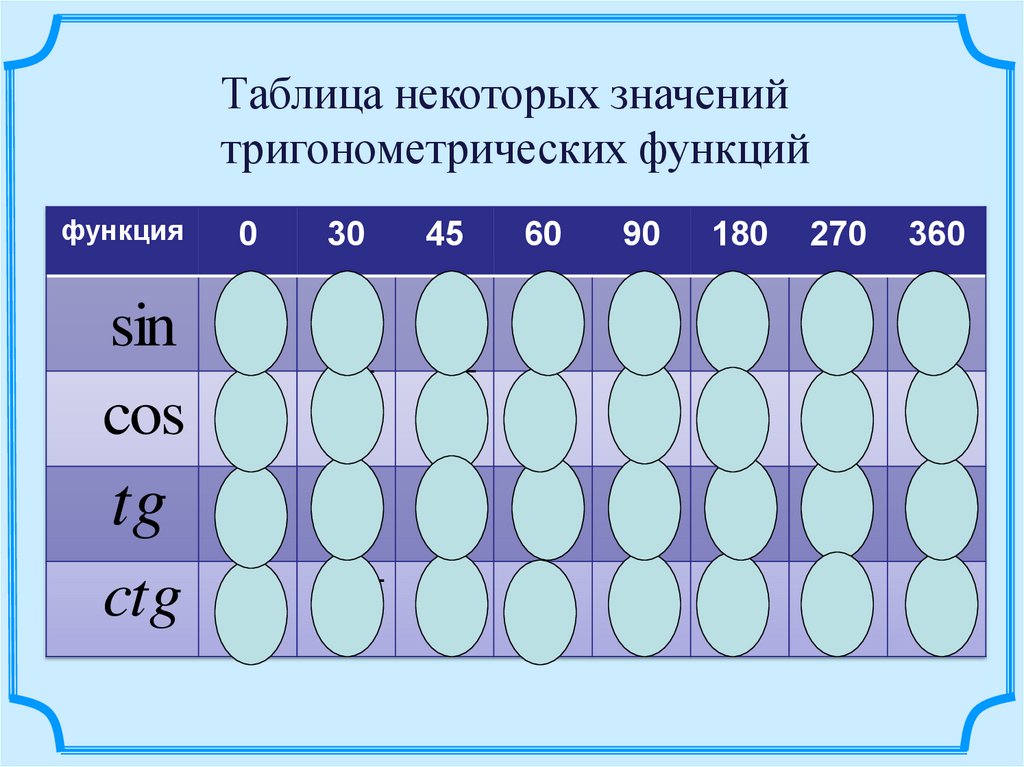
Таблица некоторых значенийтригонометрических функций
функция
0
30
45
60
sin 0
cos 1
1
2
2
2
2
2
3
2
1
2
tg 0
ctg
90
180
1 0
3
0
1
2
1
3 0
3 1
1
3 1 3 0
270
360
1 0
0 1
0
0
3.
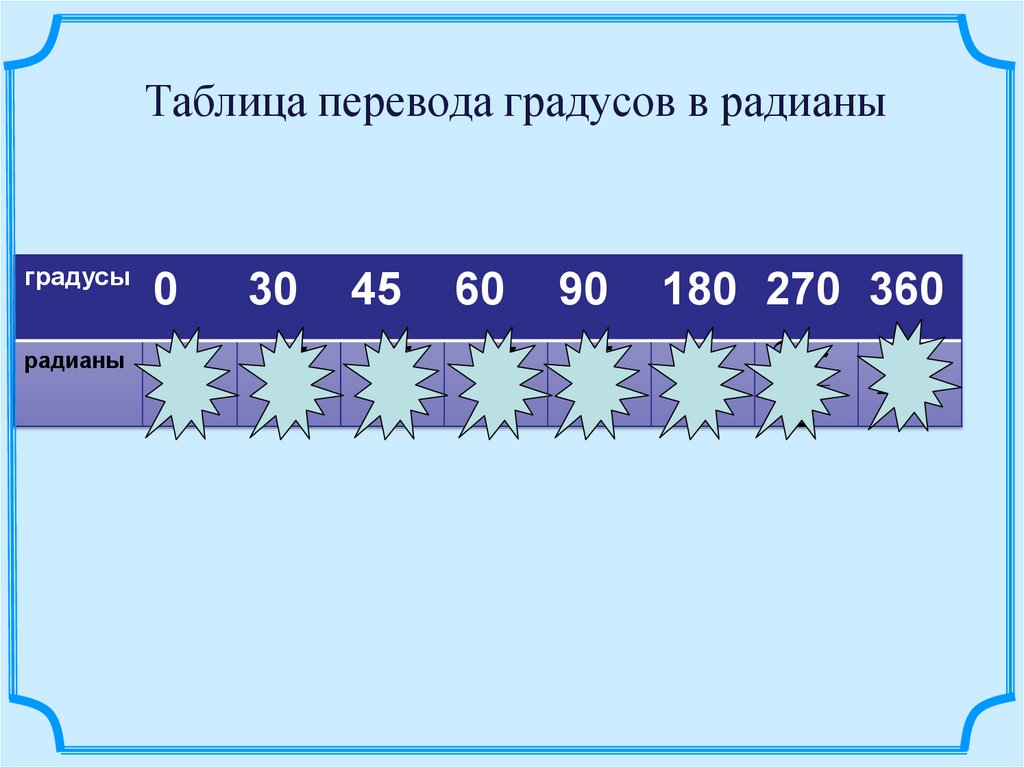
Таблица перевода градусов в радианыградусы
радианы
0
0
30
6
45
4
60
3
90
2
180 270 360
3 2
2
4.
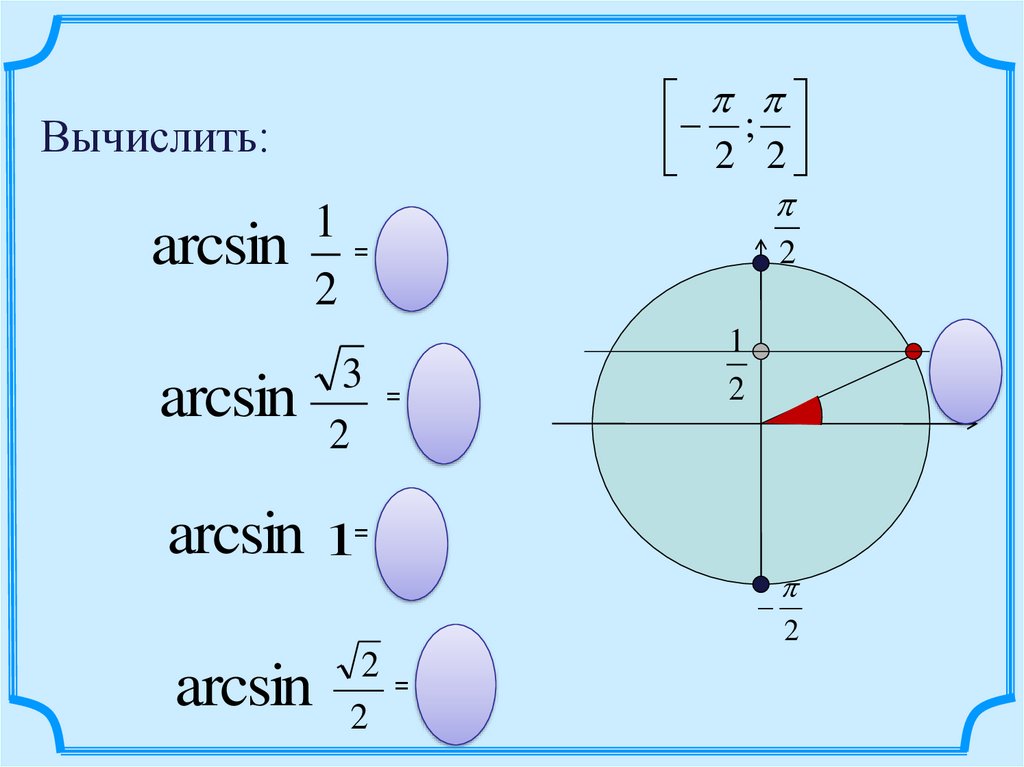
2 ; 2Вычислить:
arcsin
1
2
=
6
3
arcsin
3
2
arcsin
1=
2
arcsin
2
2
2
=
=
4
1
2
6
2
5.
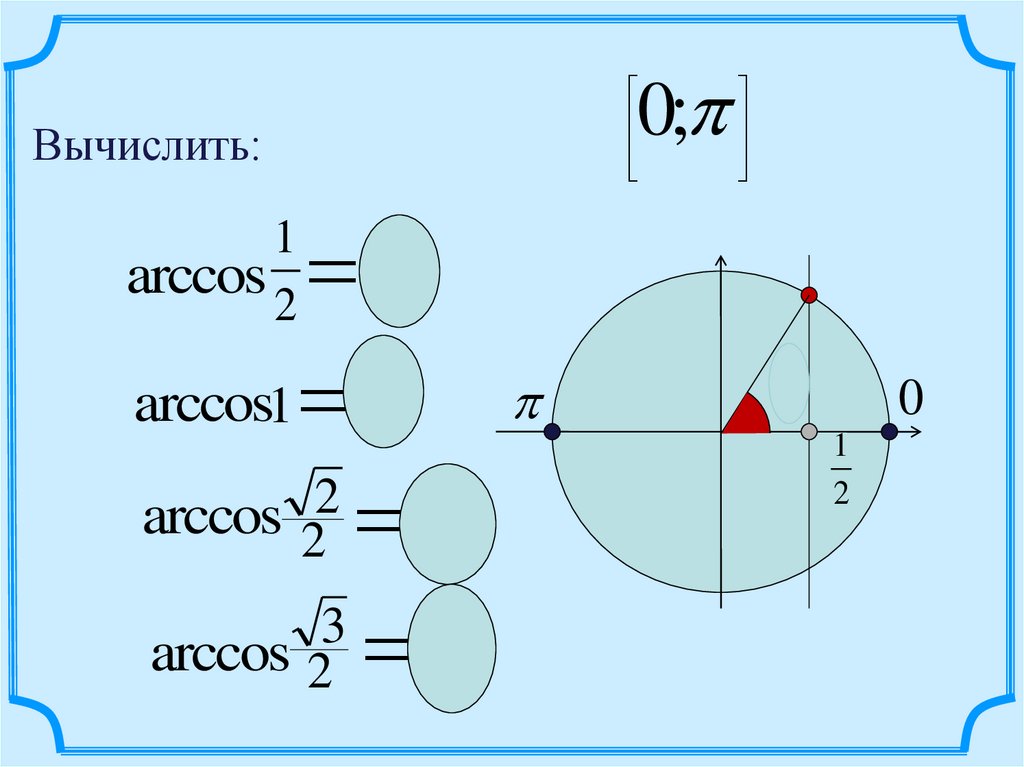
0;Вычислить:
3
arccos1 0
arccos 22
4
3
arccos 2 6
1
arccos 2
3
0
1
2
6.
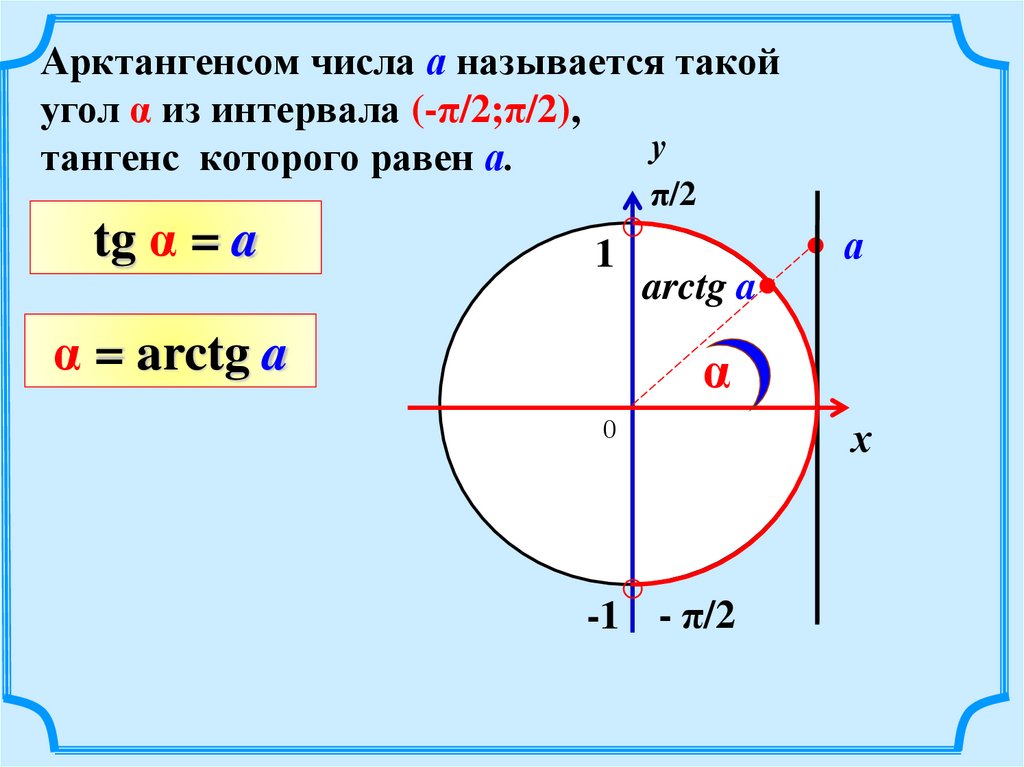
Арктангенсом числа а называется такойугол α из интервала (-π/2;π/2),
у
тангенс которого равен а.
tg α = a
1
○
π/2
а
arctg a
α = arctg a
α
0
х
○
-1 - π/2
7.
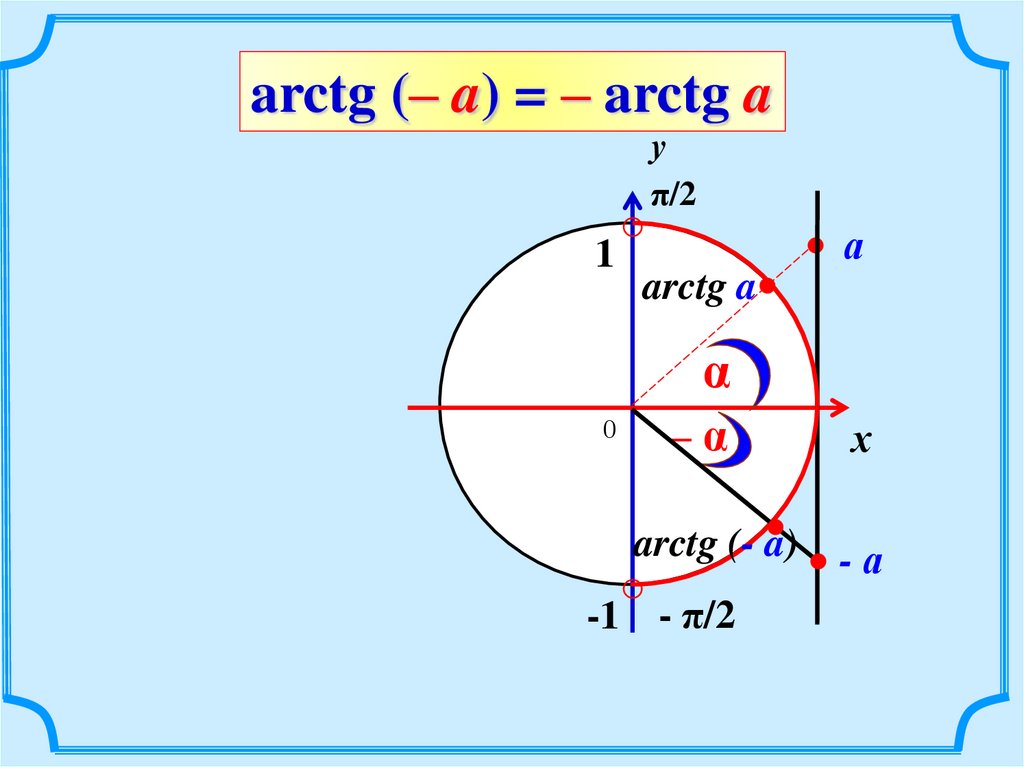
arctg (– a) = – arctg a1
○
у
π/2
а
arctg a
α
–α
0
arctg (- a)
○
-1 - π/2
х
-а
8.
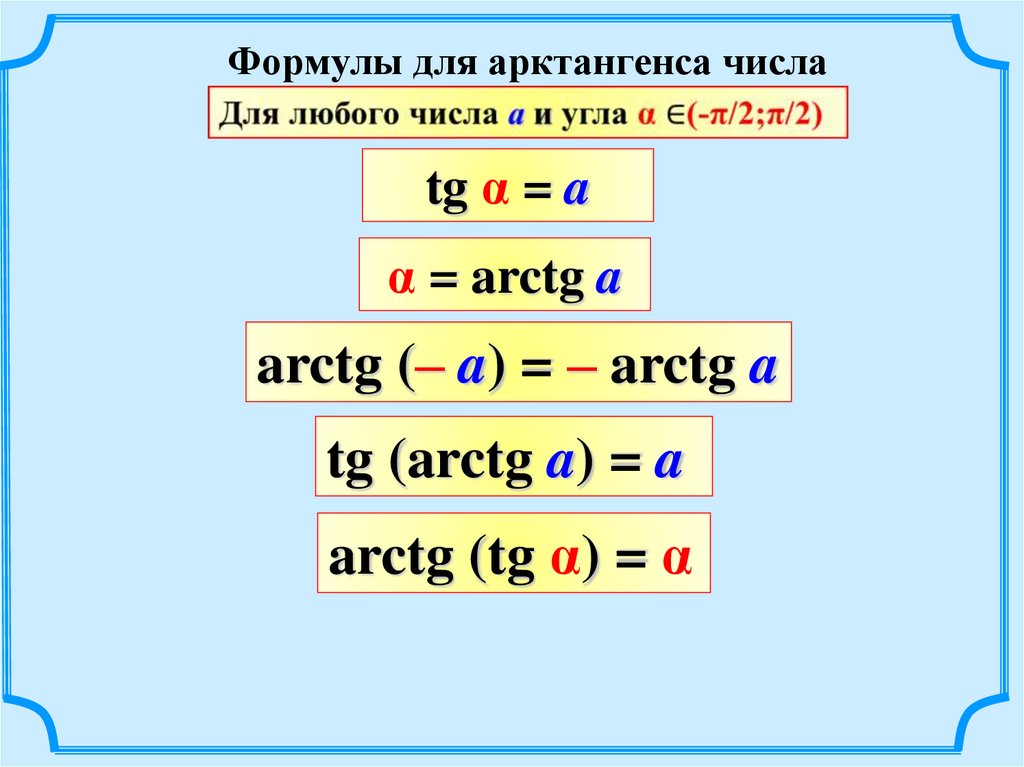
Формулы для арктангенса числаtg α = a
α = arctg a
arctg (– a) = – arctg a
tg (arctg a) = a
arctg (tg α) = α
9.
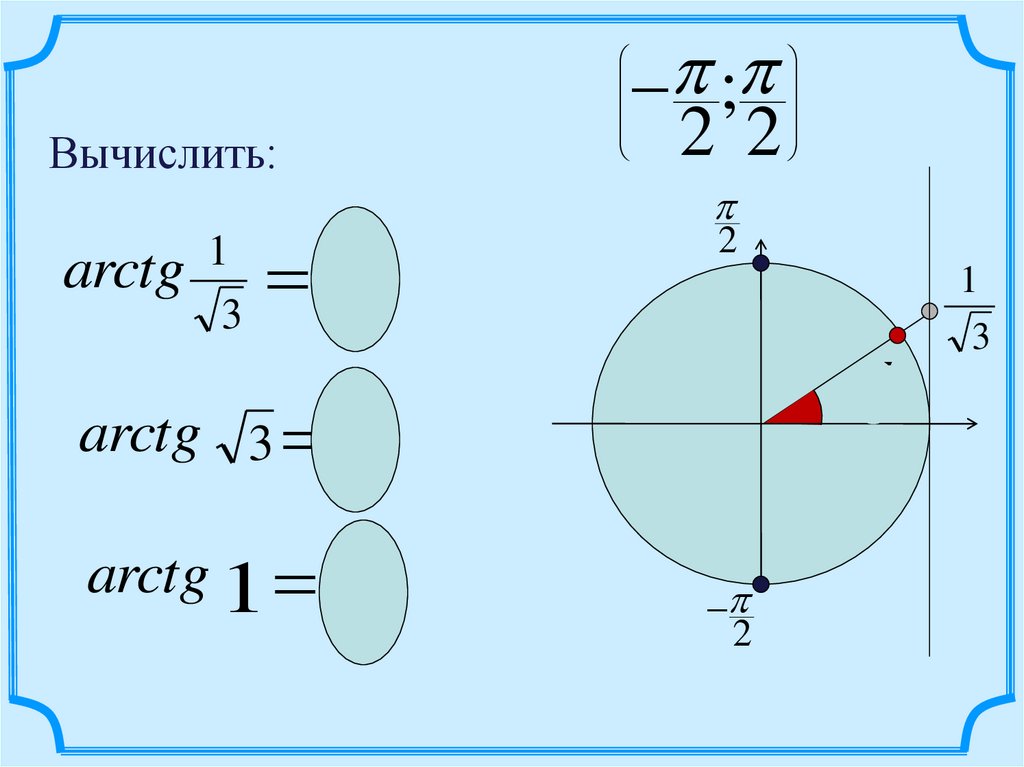
Вычислить:arctg
6
arctg 3
3
arctg 1
4
1
3
;
2 2
2
6
2
1
3
10.
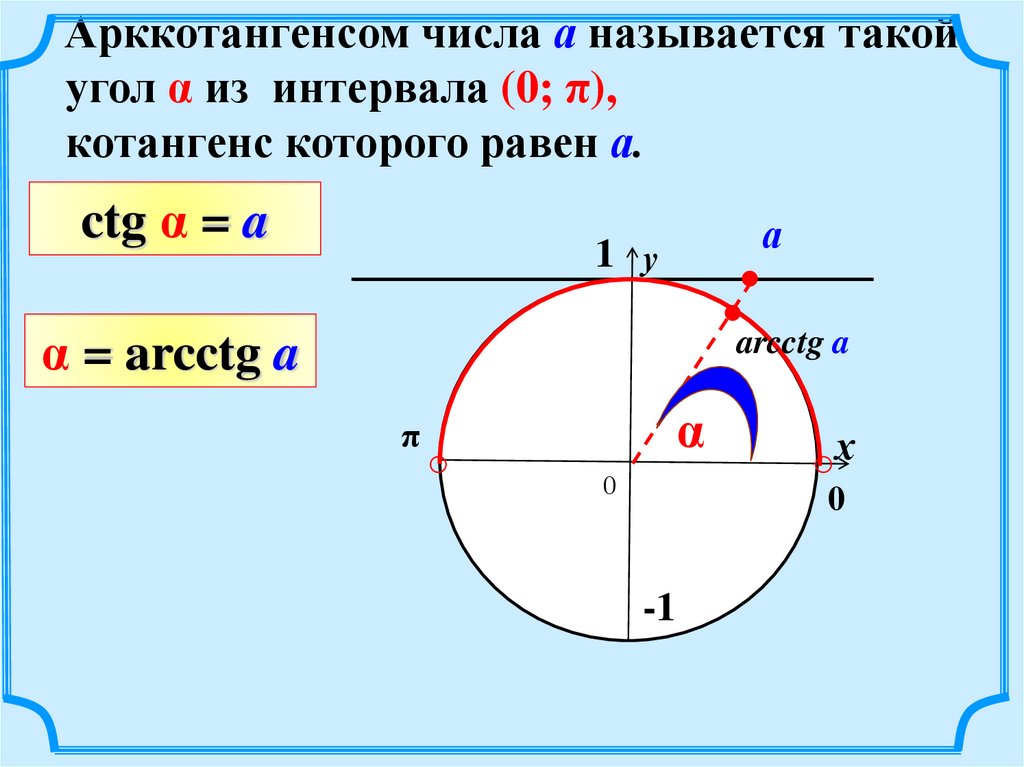
Арккотангенсом числа а называется такойугол α из интервала (0; π),
котангенс которого равен а.
ctg α = a
а
1 у
α = arcctg a
arcctg a
π
○
α
0
○х
0
-1
11.
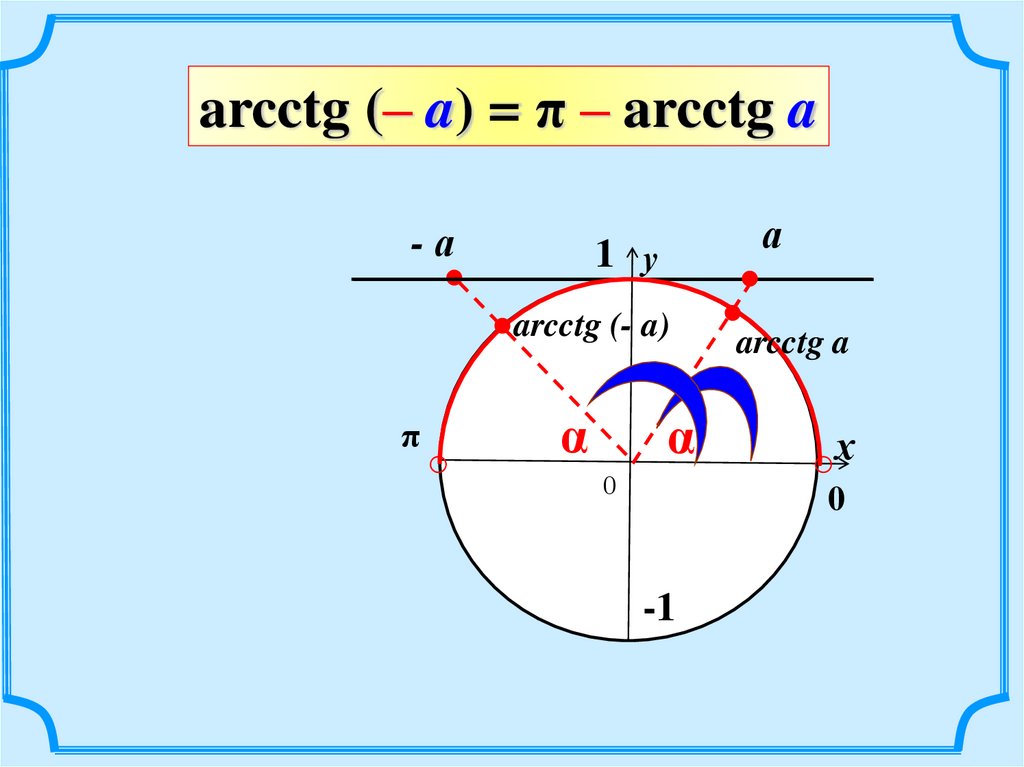
arcctg (– a) = π – arcctg a-а
а
1 у
arcctg (- a)
π
○
α
α
0
arcctg a
○х
0
-1
12.
Формулы для арккотангенса числасtg α = a
α = arсctg a
arcсtg (– a) = – arcсtg a
сtg (arcсtg a) = a
arcсtg (сtg α) = α
13.
14
0
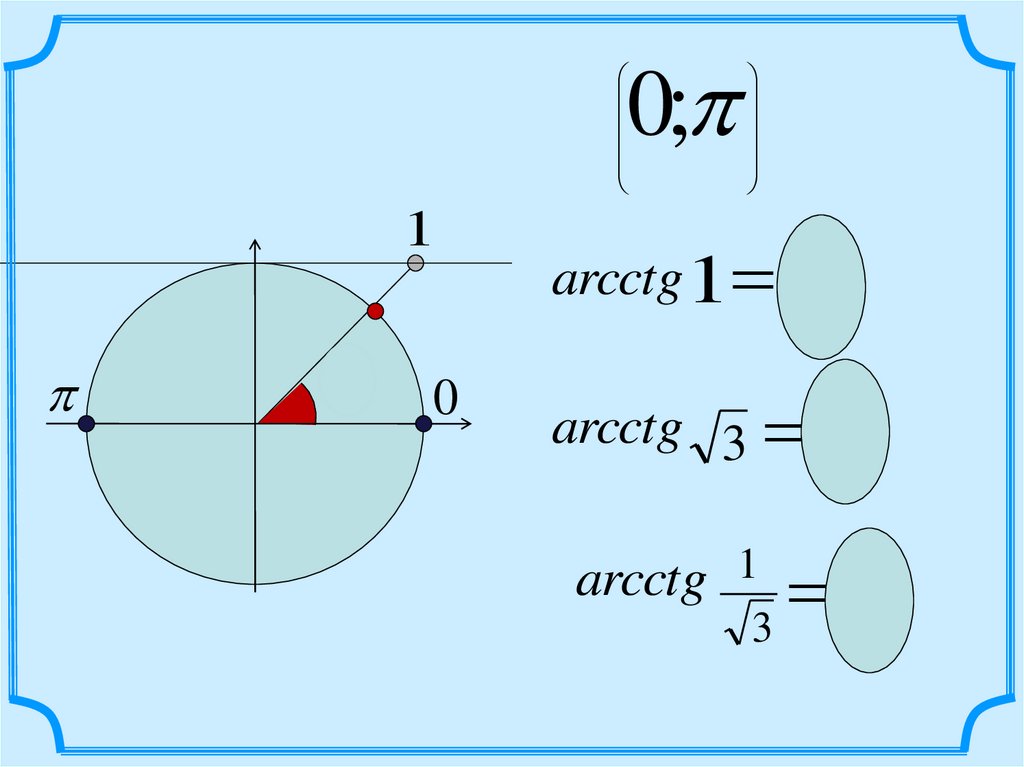
0;
arcctg1
4
arcctg 3
6
1
arcctg
3
3
14.
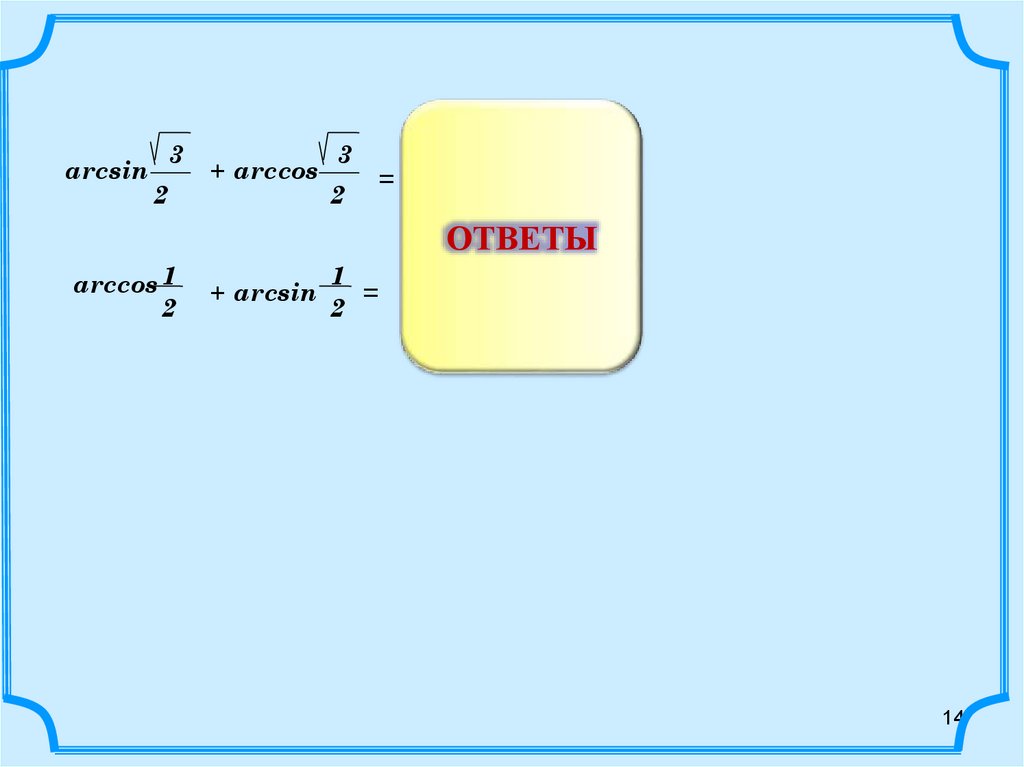
arcsin3
2
+ arccos
3
2
П
=
3
+
П
П
=
6
2
ОТВЕТЫ
arccos 1
2
+ arcsin
1
=
2
П
+ П = П
6
2
3
14
15.
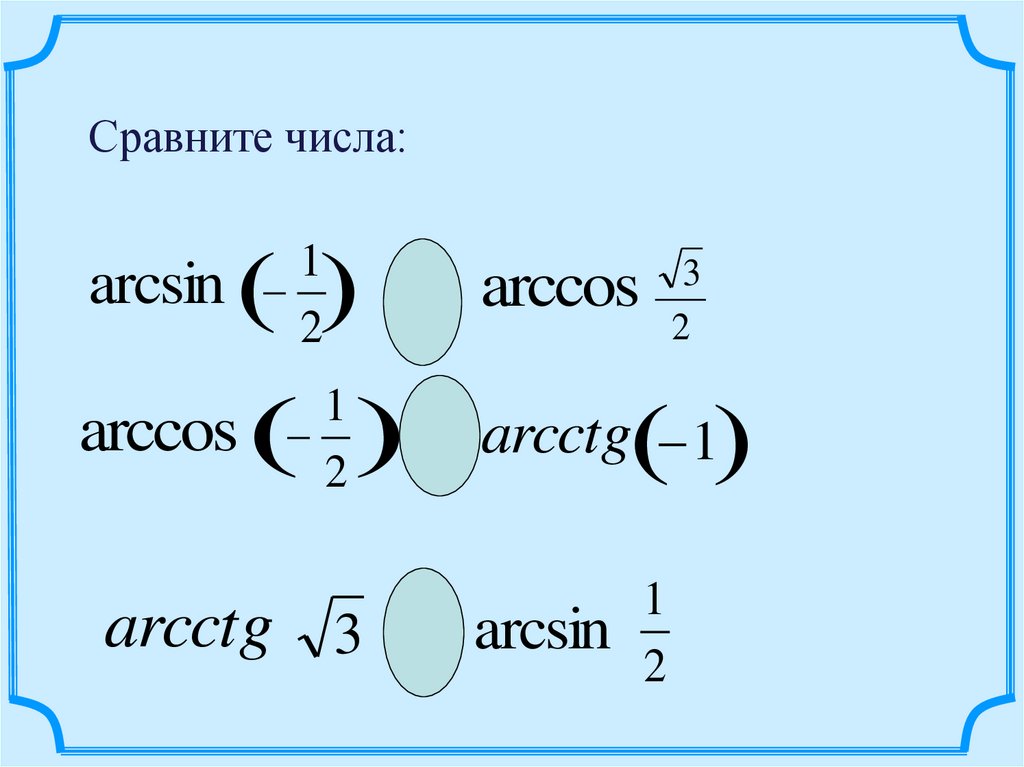
Сравните числа:1
arccos arcctg 1
2
arcsin
1
2
arcctg 3
3
2
arccos
arcsin
1
2
16.
Вычислить2arcsin
arctg 1 arccos 23
2
2
3
2
arcctg
1
1
3arcsin 2 4arccos 2
8
3
3




 Математика
Математика








