Похожие презентации:
Арктангенс и арккотангенс. Решение уравнений
1.
Арктангенс и арккотангенсРешение уравнений
tgx=a, ctgx=a
2.
tgx 2Решить уравнение
х1
arctgb x
x x1 k, k Z
x arctg 2 k , k Z
x ;
2 2
3. Определение арктангенса и арккотангенса
Арктангенс а – это такое число из интервала; , тангенс которого равен а
2 2
tgx a
arctga x
x 2 ; 2
а R
3
3
Вычислить: arctg
, х
х tgx
3
3
6
3
arctg
3
6
4.
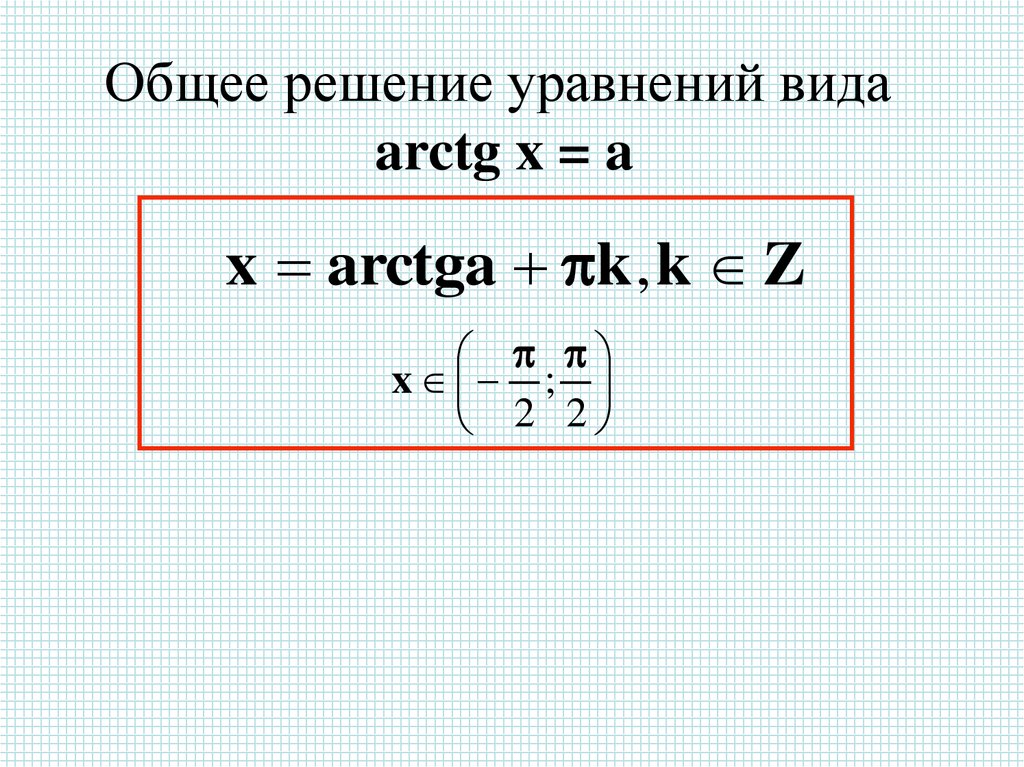
Общее решение уравнений видаarctg x = a
x arctga k , k Z
x ;
2 2
5.
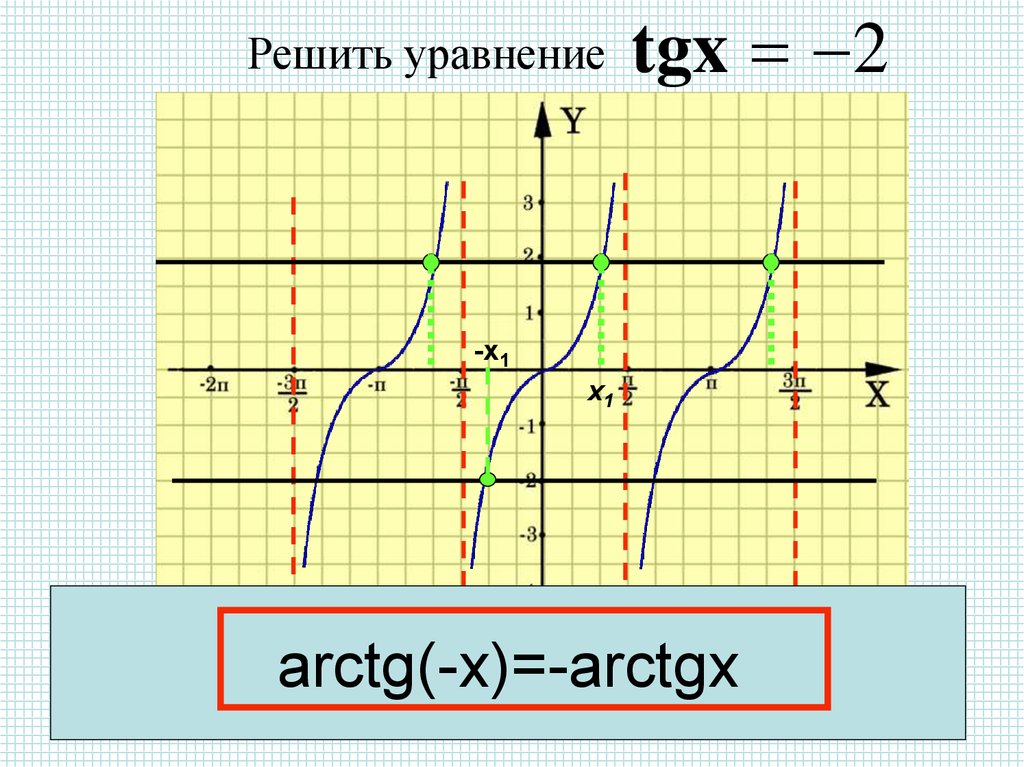
Решить уравнениеtgx 2
-x1
х1
arctgb x
arctg(-x)=-arctgx
6.
Решить уравнениеРешение:
tgx 1
tgx 1
x arctg1 k , k Z
x k , k Z
4
Ответ:
x k , k Z
4
7.
Решить уравнение tgxРешение:
3
tgx 3
x arctg 3 k , k Z
x k , k Z
3
Ответ:
x k , k Z
3
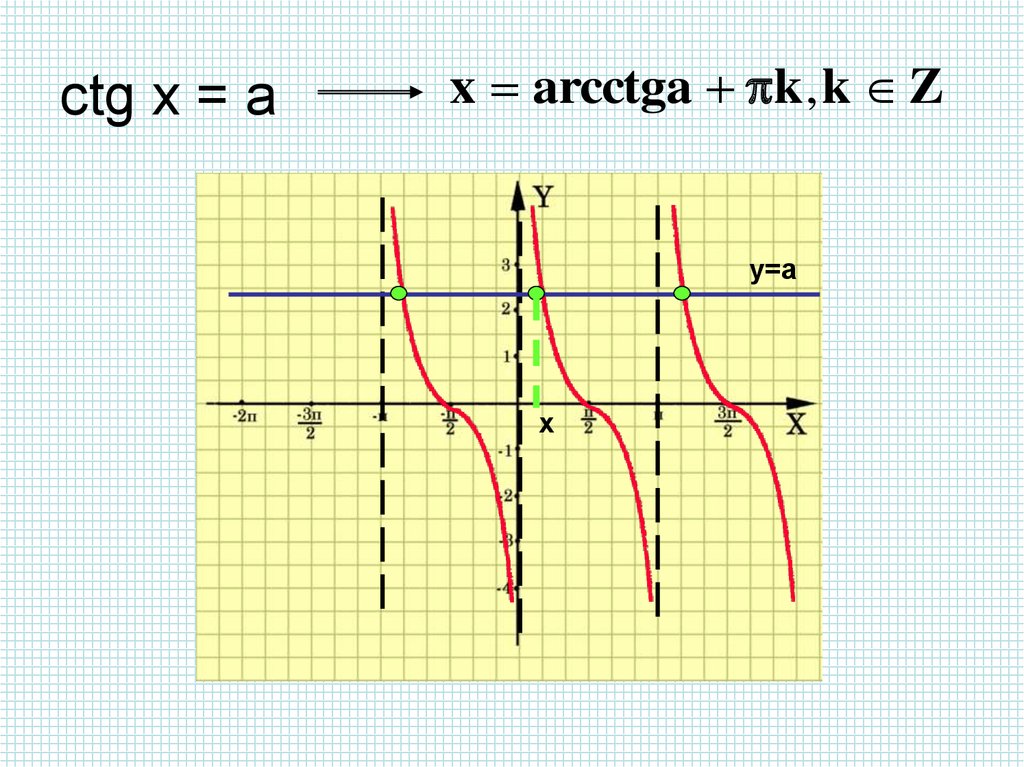
8. ctg x = a
x arcctga k , k Zy=a
x arcctga k , k Z
x arcctga k , k Z
x
9.
Арккотангенс а – это такое число из интервала(0; п), котангенс которого равен а
ctgx a,
arcctga x
x 0;
а R
Вычислить: arcctg 3
x
6
х ctgx 3
arcctg 3
6
10.
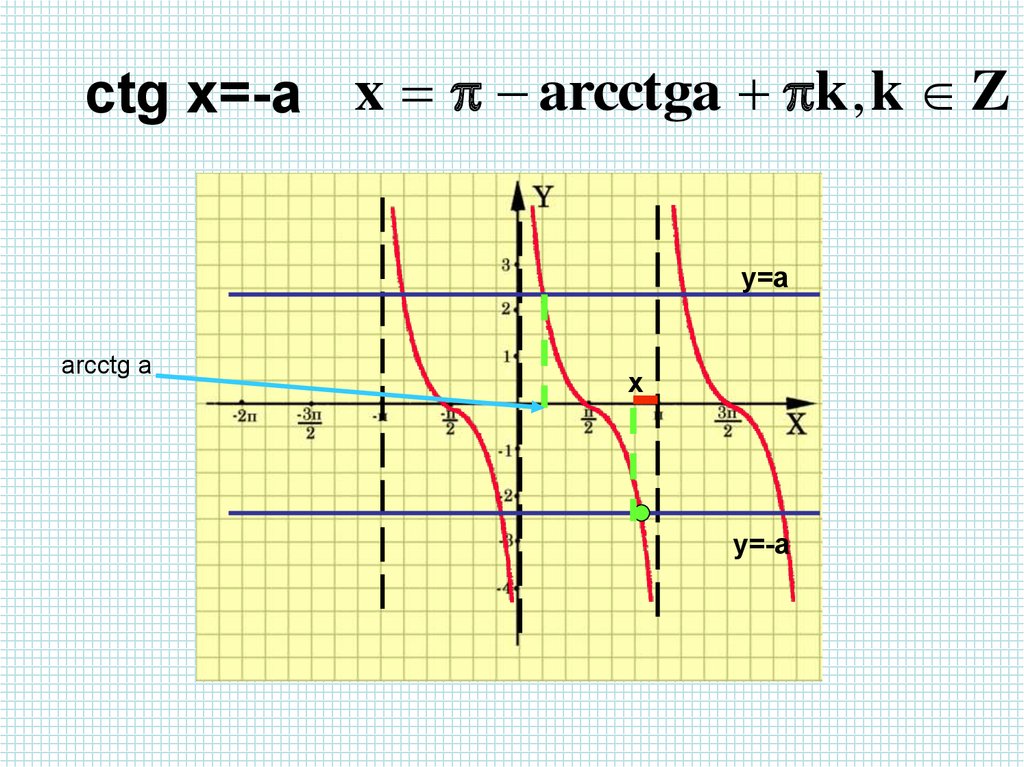
ctg x=-a x arcctga k , k Zy=a
x arcctga k , k Z
arcctg a
x
x arcctga k , k Z
y=-a
11.
Общее решение уравнений видаctgx=a
x arcctga k , k z
arcctg ( a) arcctga
12. ctg x = √3
Решение:ctgx 3
x arcctg 3 k, k Z
x k , k Z
6
Ответ:
x k , k Z
6
13.
3ctgx
3
Решение:
3
ctgx
3
3
k , k z
x arcctg
3
3
x arcctg
k , k Z
3
x k , k Z
3
2
x
k , k Z
3
2
Ответ: x
k , k Z
3







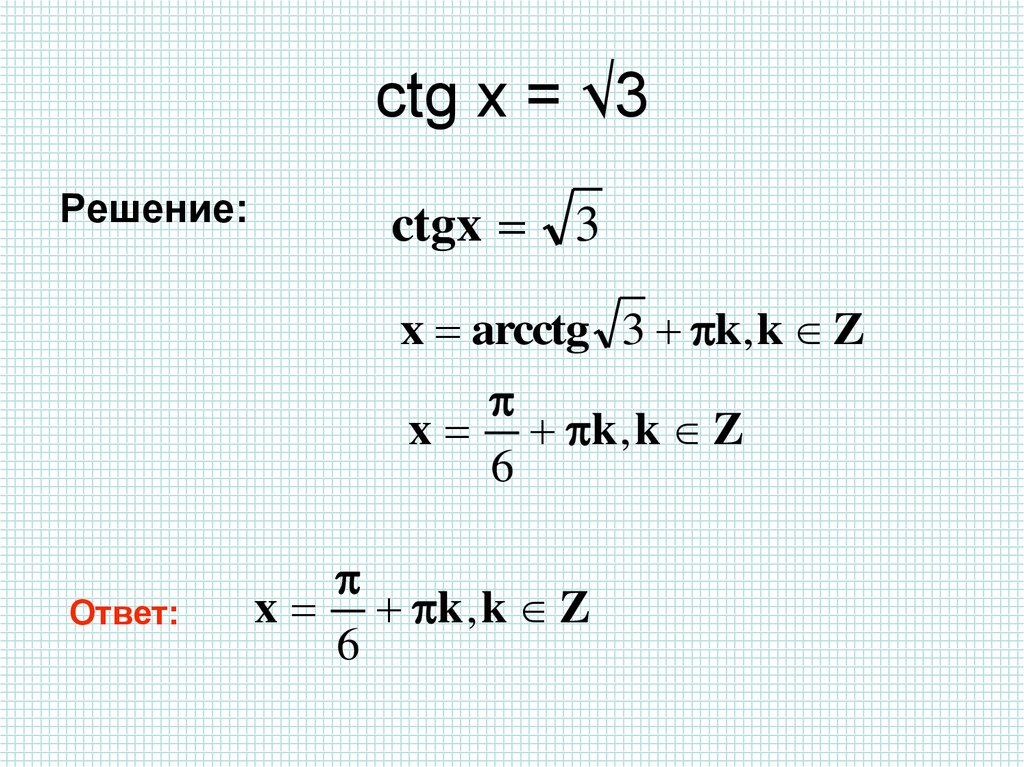

 Математика
Математика








