Площадь криволинейной трапеции и интеграл

1.

у
х

2.

Криволинейная трапеция
Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].
У
0
a
x=b
х=а
y = f(x)
b
Х
Отрезок [a;b] называют основанием
этой криволинейной трапеции

3.

Криволинейная трапеция
х
у
1
У=х²+2х
-2
0
2
у 2
-1
0 1
-1
0
х
-1
0
2

4.

Какие из заштрихованных на рисунке
фигур являются криволинейными
трапециями, а какие нет?
Заполнить таблицу
№1
№2
№3
№4
№5
№6
Да/нет

5.

2
1
Не верно
верно
у
3
у
у
y = f(x)
y = f(x) 3
y = f(x)
У=1
0
0
0
х
4
5
у
верно
х
6
у
y = f(x)
х
y = f(x)
у
y = f(x)
У=3
0
0
х
Не верно
0
х
х
верно
Не верно

6.

Изобразить криволинейную трапецию,
ограниченную графиком функции y = (x-1)2,
осью Ox и прямой x=2.
y x 1
2
1
0
1
01
x=2
y
12
x

7.

Определенный интеграл
b
b
f
(
x
)
dx
F
(
x
)
F
(
b
)
F
(
a
)
a
a
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла заключается в
том, что определенный интеграл равен площади криволинейной
трапеции, образованной линиями:
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.

8.

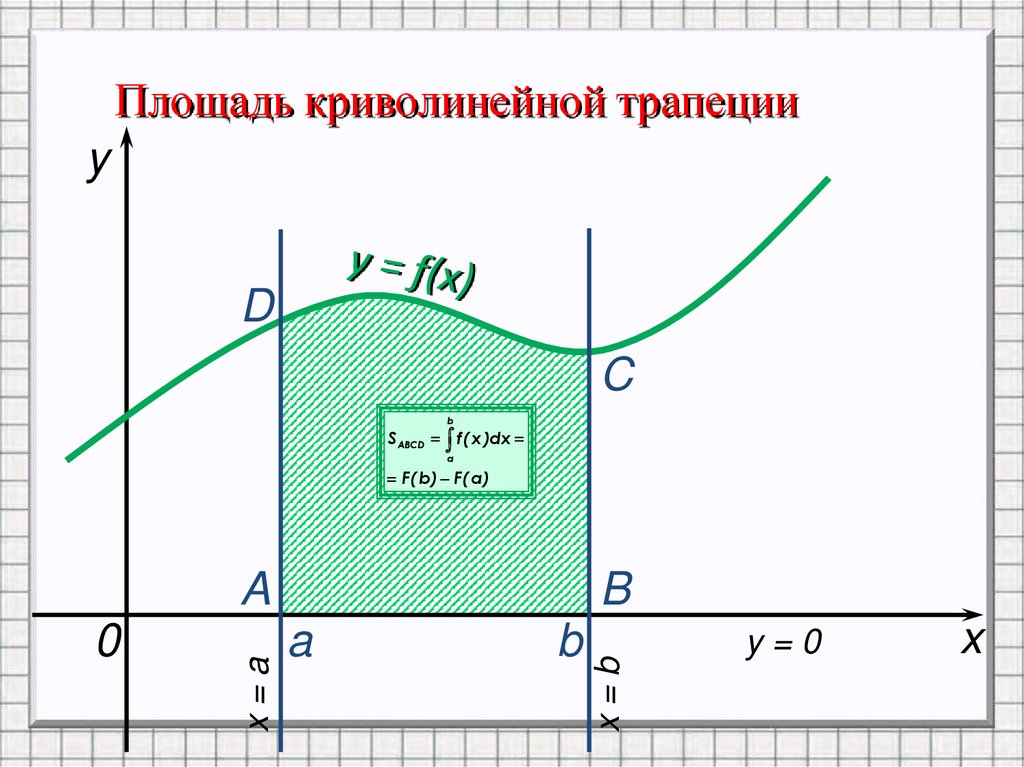
Площадь криволинейной трапеции
y
D
C
b
S ABCD f ( x )dx
a
F( b ) F( a )
B
a
b
x=b
0
x=a
A
y=0
x

9.

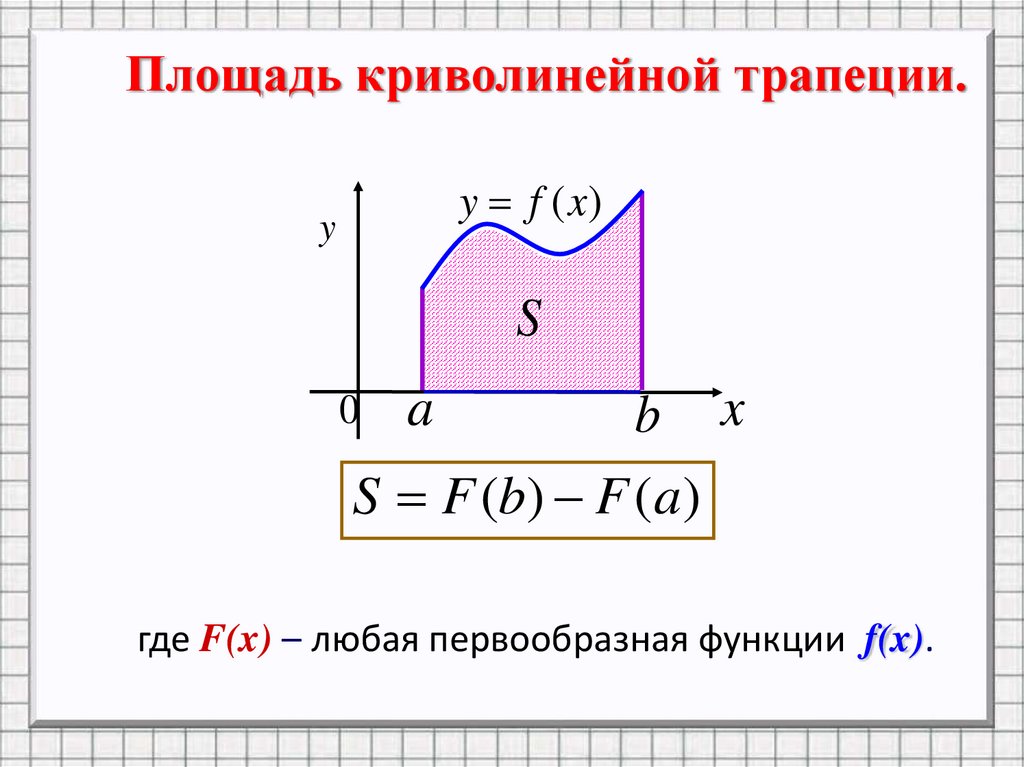
Площадь криволинейной трапеции.
y f (x)
y
S
0
a
b
x
S F (b) F (a)
где F(x) – любая первообразная функции f(x).

10.

Формула Ньютона-Лейбница
S F (b) F (a)
b
f ( x)dx F (b) F (a)
a
b
1643—1727
f ( x)dx F (b) F (a)
a
b
S f ( x)dx
a
1646—1716

11.

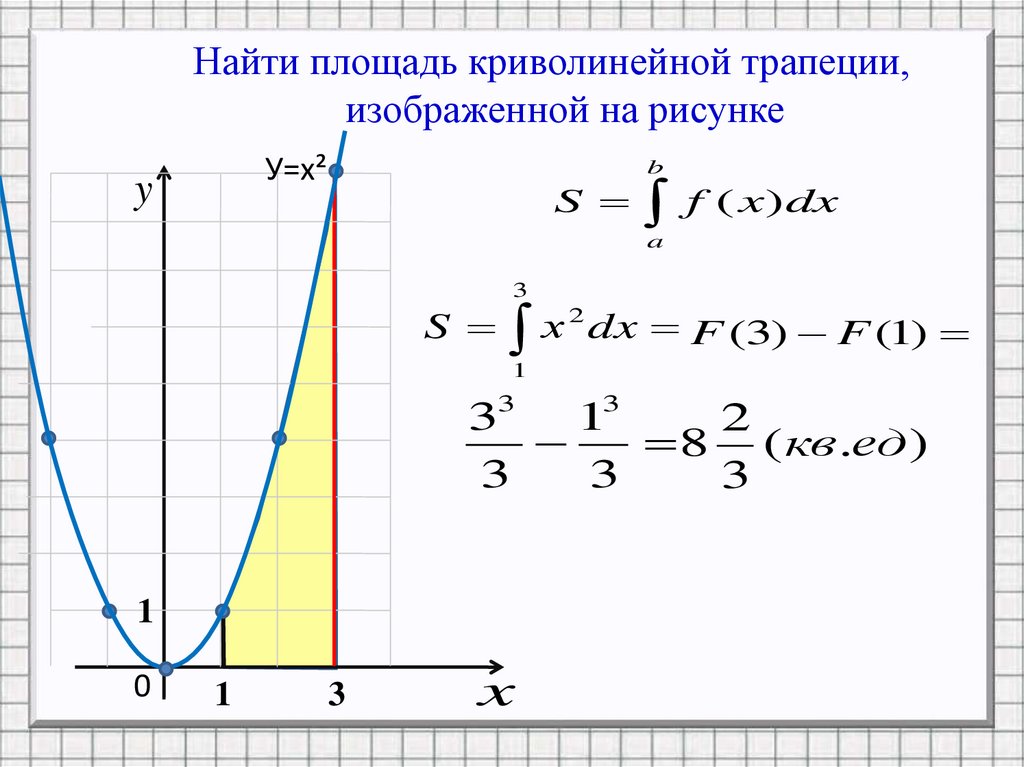
Найти площадь криволинейной трапеции,
изображенной на рисунке
У=х²
y
b
S
f ( x) dx
a
3
S
х 2 dx F (3) F (1)
1
33 13
2
8 ( кв .ед)
3
3
3
1
0
1
3
x