Похожие презентации:
Площадь криволинейной трапеции и интеграл
1.
Площадькриволинейной
трапеции и интеграл.
2.
Площадь криволинейной трапеции.y f (x)
y
S
0
a
b
S F (b) F (a )
где F(x) – любая первообразная функции f(x).
x
3.
Формула Ньютона-ЛейбницаS F (b) F (a )
b
f ( x)dx F (b) F (a)
a
b
1643—1727
f ( x)dx F (b) F (a)
a
b
S f ( x)dx
a
1646—1716
4.
Формула Ньютона-ЛейбницаАлгоритм вычисления площади
криволинейной трапеции:
F(x)=… …
S=F(b) – F(a)=… …
1.
Схематично изобразить график
функции f(x).
2.
Провести прямые x=a и x=b.
3.
Записать одну из
первообразных F(x)
функции f(x).
4.
Составить и вычислить
разность
F(b) – F(a).
5.
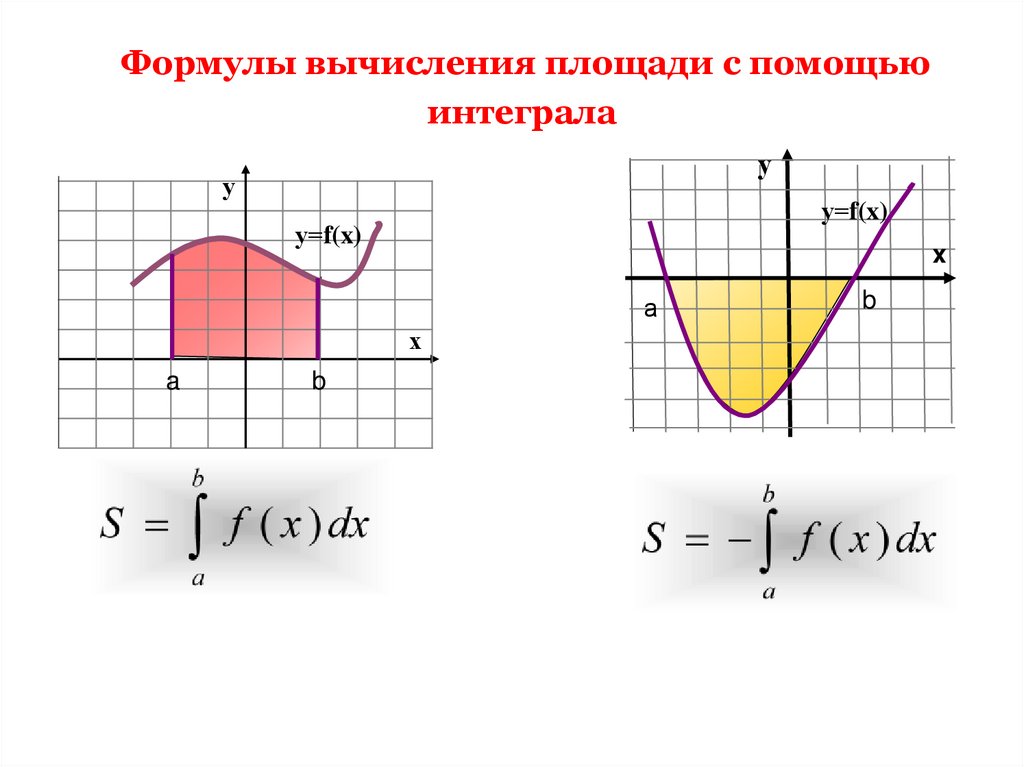
Формулы вычисления площади с помощьюинтеграла
у
у
у=f(x)
у=f(x)
x
а
х
a
b
b
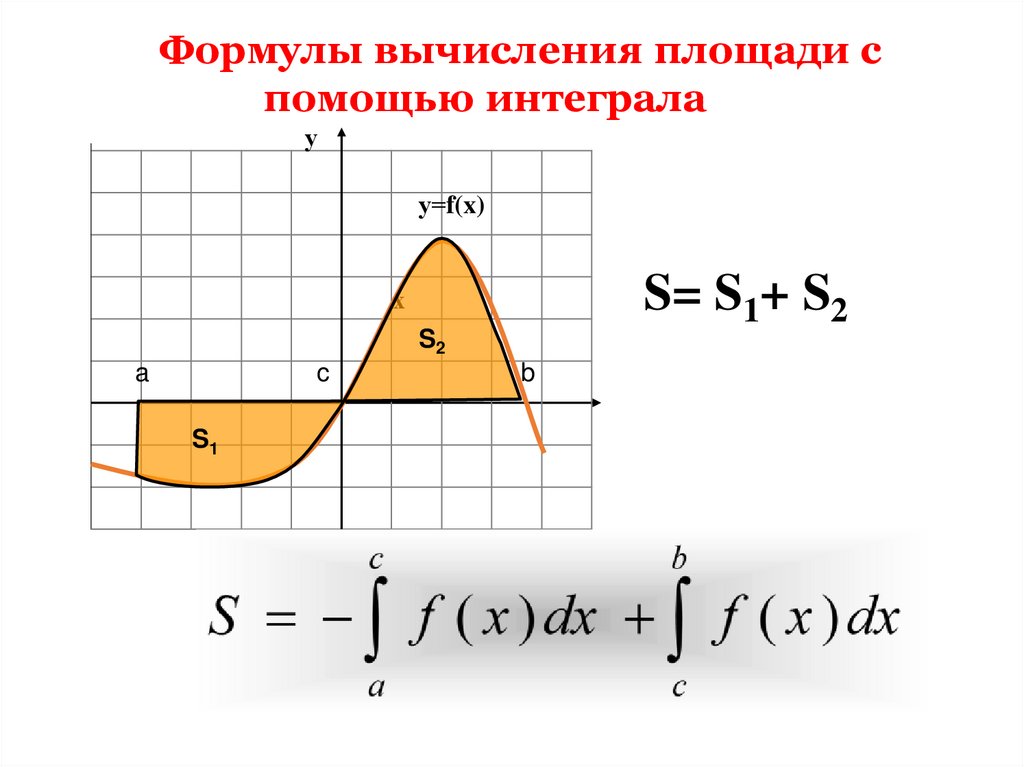
6.
Формулы вычисления площади спомощью интеграла
у
у=f(x)
S= S1+ S2
х
S2
a
c
S1
b
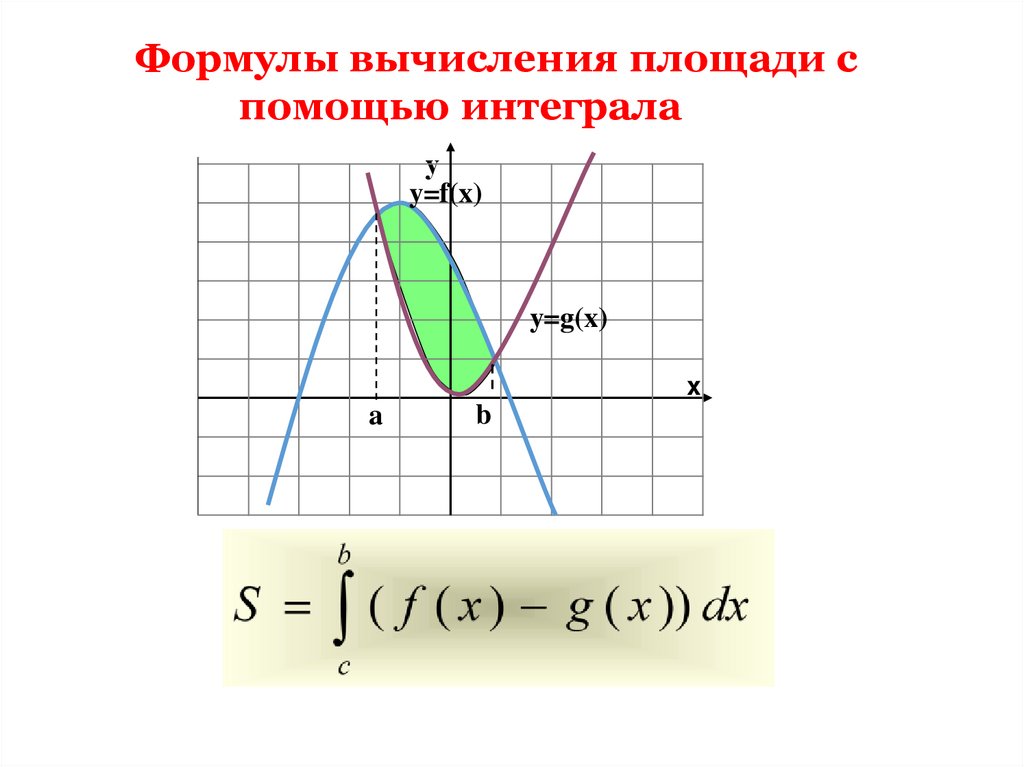
7.
Формулы вычисления площади спомощью интеграла
у
y=f(x)
y=g(x)
x
a
b
8.
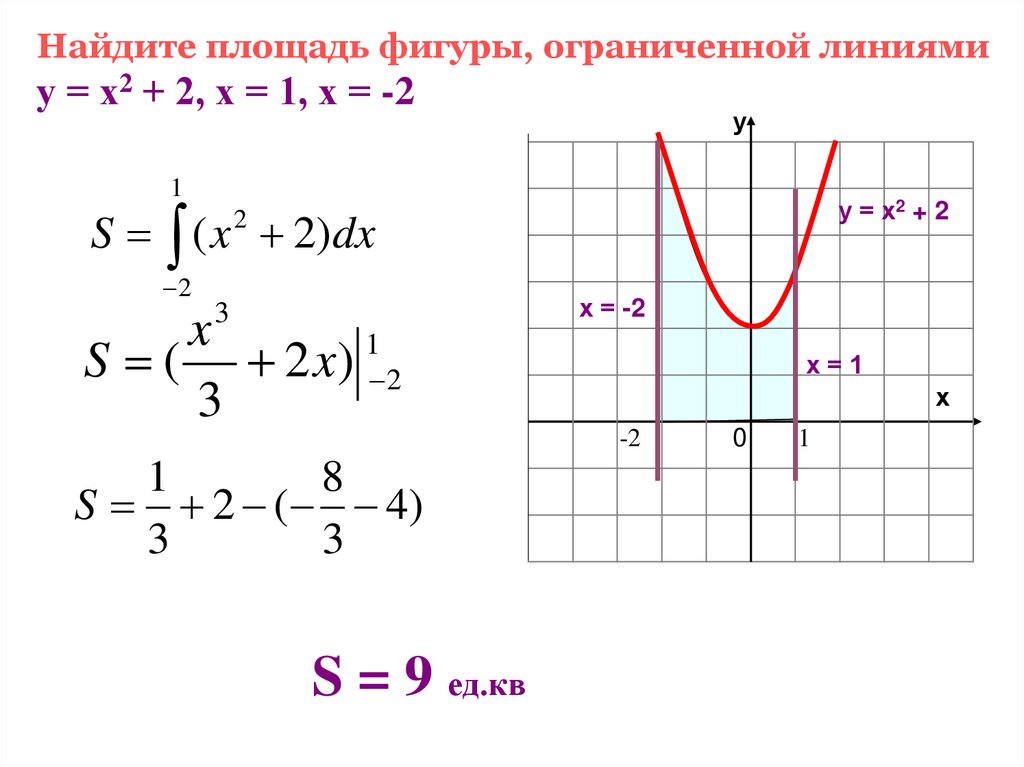
Найдите площадь фигуры, ограниченной линиямиу = х2 + 2, х = 1, х = -2
у
1
S ( x 2)dx
у = х2 + 2
2
2
3
x
1
S ( 2 x) 2
3
х = -2
х=1
х
-2
1
8
S 2 ( 4)
3
3
S = 9 ед.кв
0
1
9.
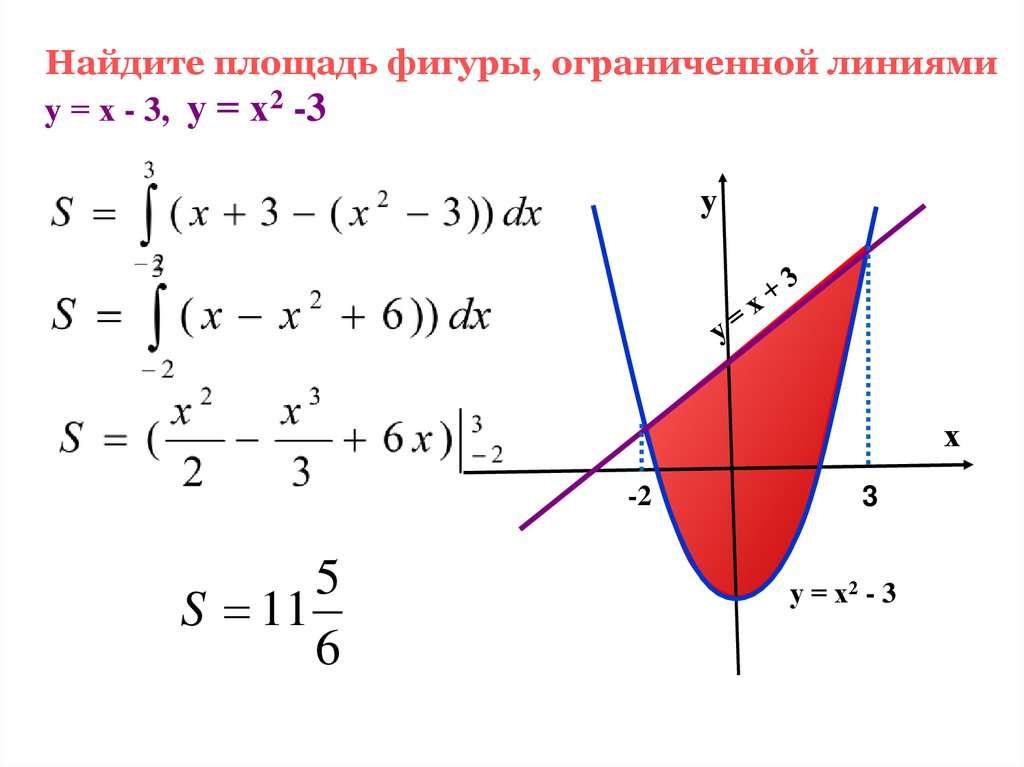
Найдите площадь фигуры, ограниченной линиямиу = х - 3, у = х2 -3
у
х
-2
5
S 11
6
3
у = х2 - 3
10.
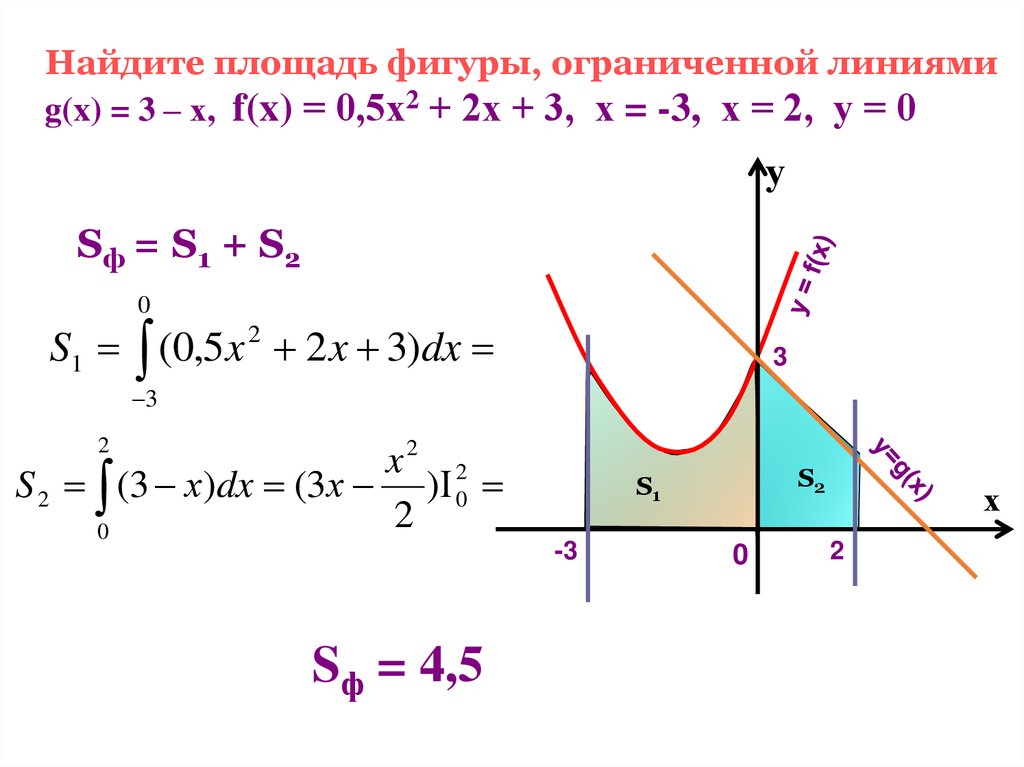
Найдите площадь фигуры, ограниченной линиямиg(x) = 3 – х, f(x) = 0,5х2 + 2х + 3, х = -3, х = 2, у = 0
у
Sф = S1 + S2
0
S1 (0,5 x 2 2 x 3)dx
3
3
2
x2 2
S 2 (3 х)dx (3х ) 0
2
0
Sф = 4,5
S2
S1
-3
0
х
2
11.
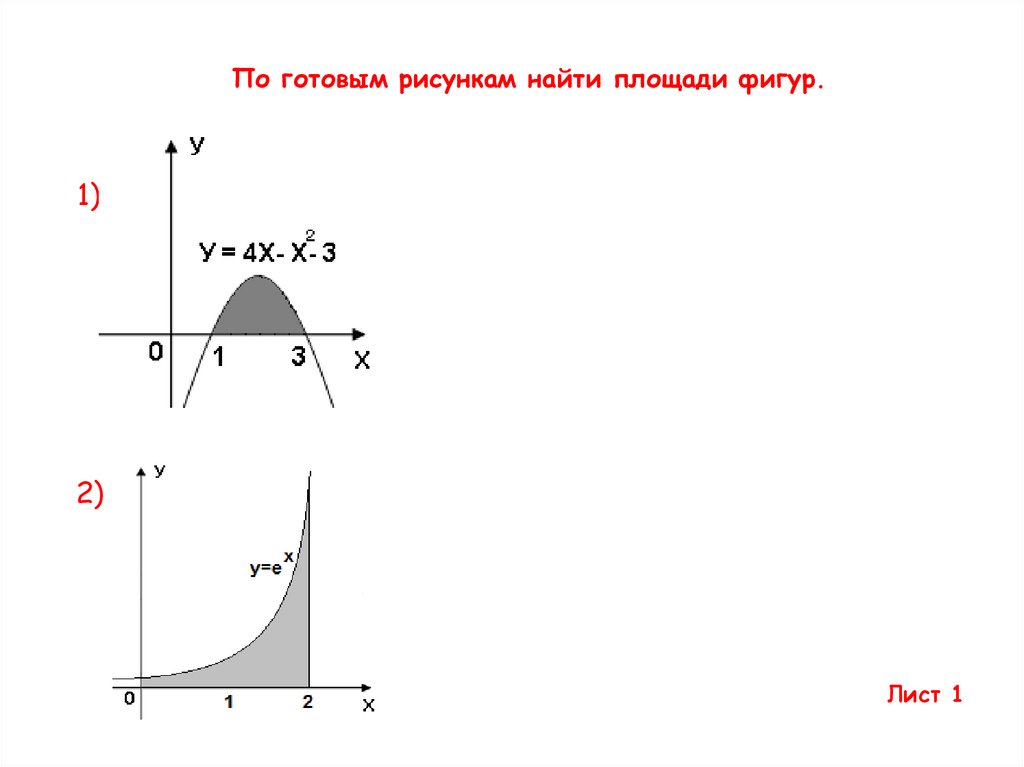
По готовым рисункам найти площади фигур.1)
2)
Лист 1
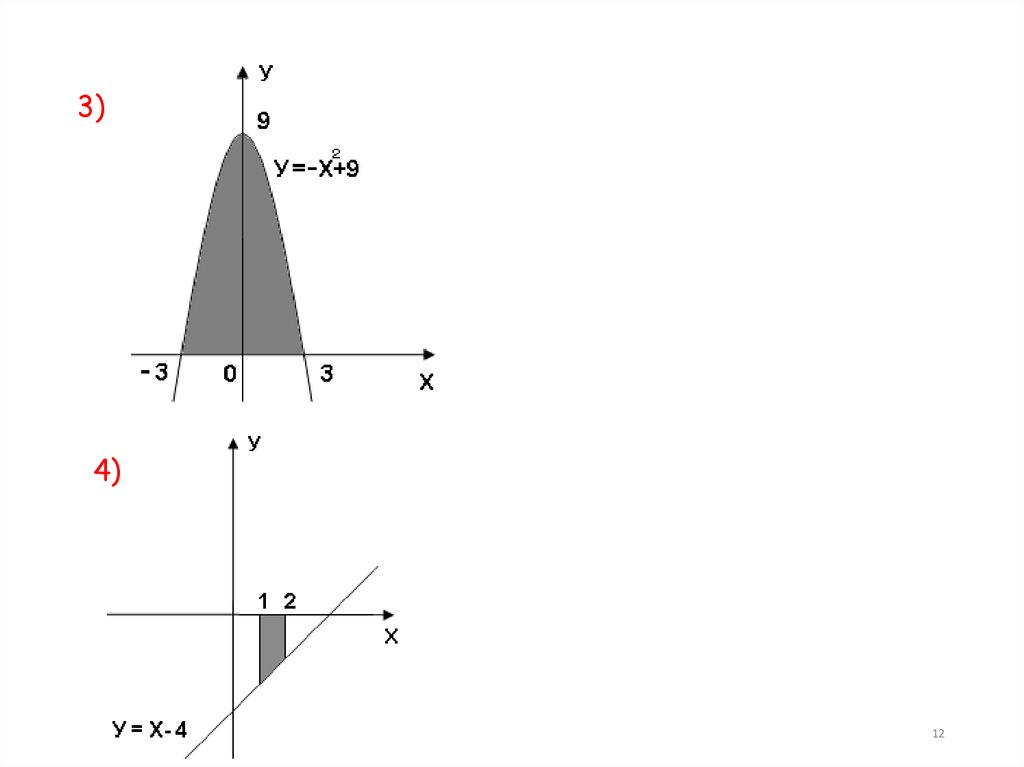
12.
3)4)
12
13.
Задания для закрепления материала1)
3)
2)
4)
14.
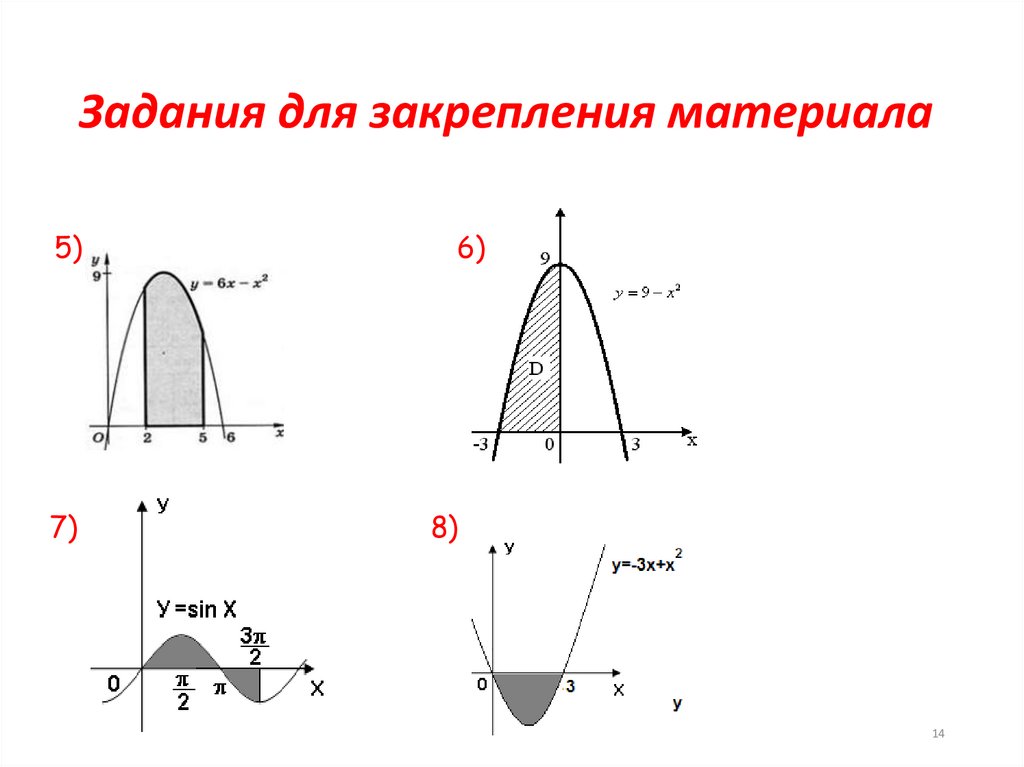
Задания для закрепления материала5)
7)
6)
8)
14
15.
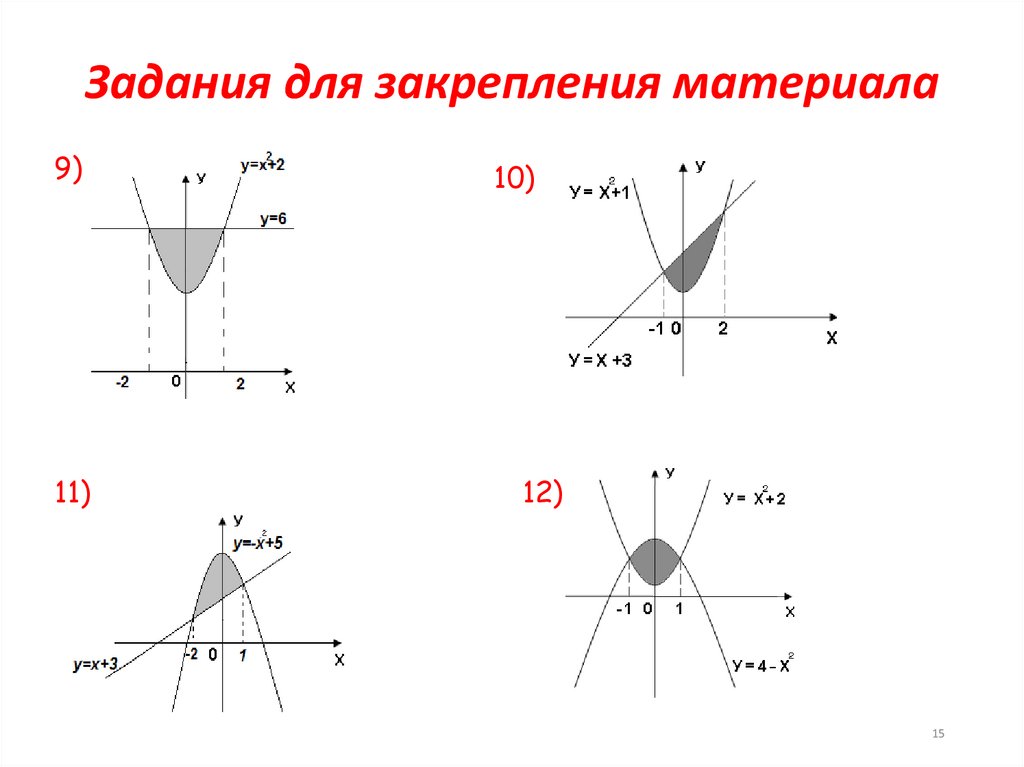
Задания для закрепления материала9)
11)
10)
12)
15





 Математика
Математика








