Площадь криволинейной трапеции и интеграл

1.

Алгебра
«Площадь криволинейной трапеции и интеграл»

2.

Задачи
Рассмотреть криволинейную трапецию
Ввести понятие «интеграл» и его геометрический
смысл
Описать нахождение площади криволинейной
трапеции с помощью формулы Ньютона-Лейбница
Уметь грамотно читать математические записи
Цель урока:
• Рассмотреть применение
первообразной для
нахождения площади
криволинейной трапеции и
познакомиться со
свойствами интеграла

3.

Определение
Криволинейная трапеция
фигура, ограниченная графиком
непрерывной и не меняющей знак
функции f(х), с помощью прямых
х=а, x=b и отрезка [а;b].

4.

Определение
Название
слайда
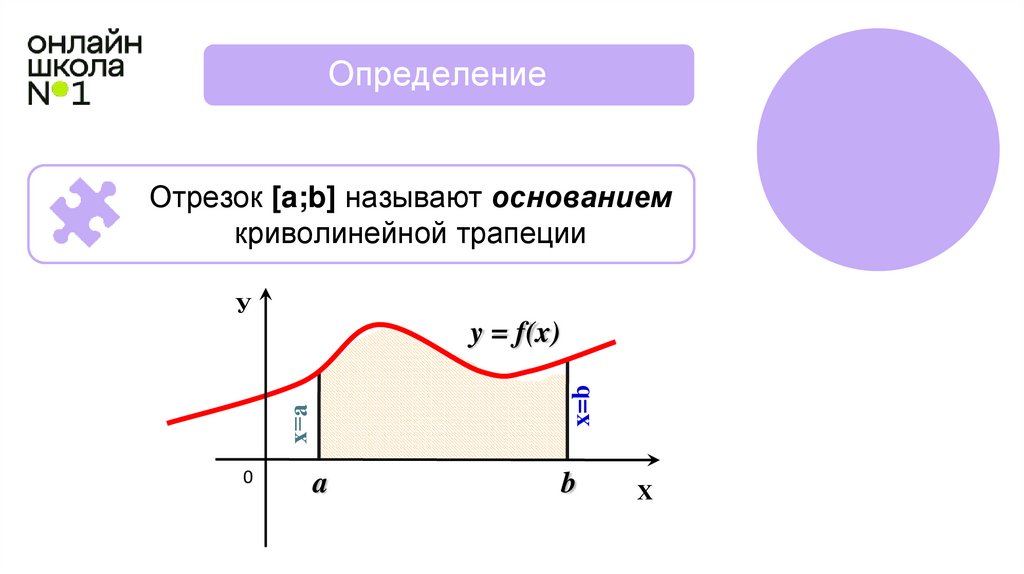
Отрезок [a;b] называют основанием
криволинейной трапеции
У
х=а
x=b
y = f(x)
0
a
b
Х

5.

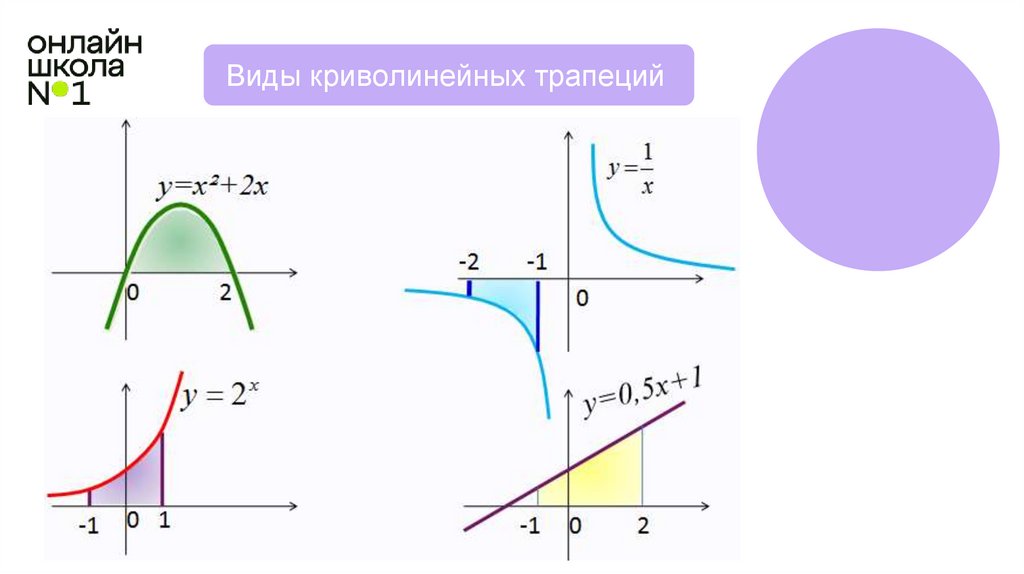
Виды криволинейных трапеций

6.

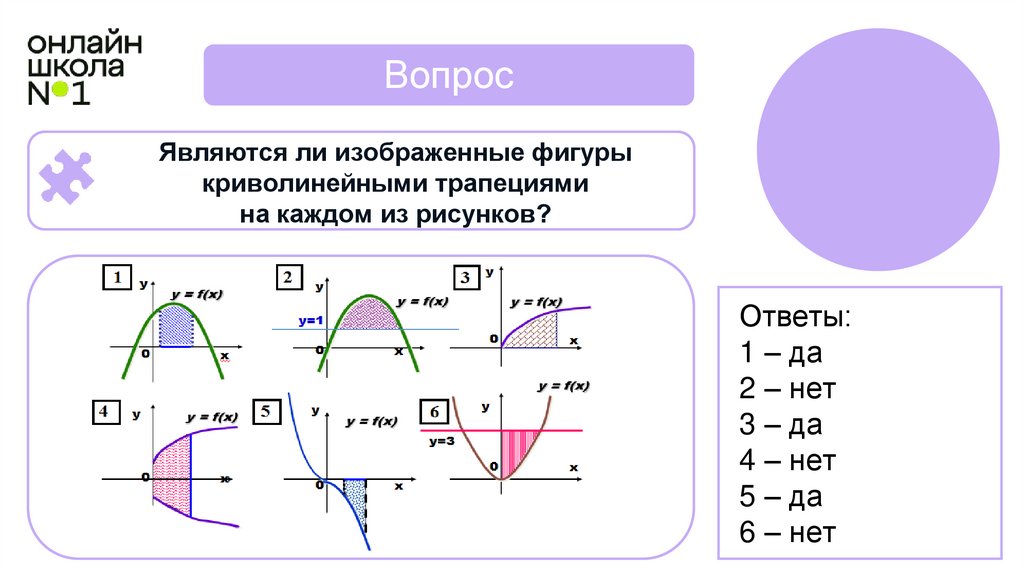
Вопрос
Являются ли изображенные фигуры
криволинейными трапециями
на каждом из рисунков?
Ответы:
1 – да
2 – нет
3 – да
4 – нет
5 – да
6 – нет

7.

Криволинейная
трапеция
Название слайда
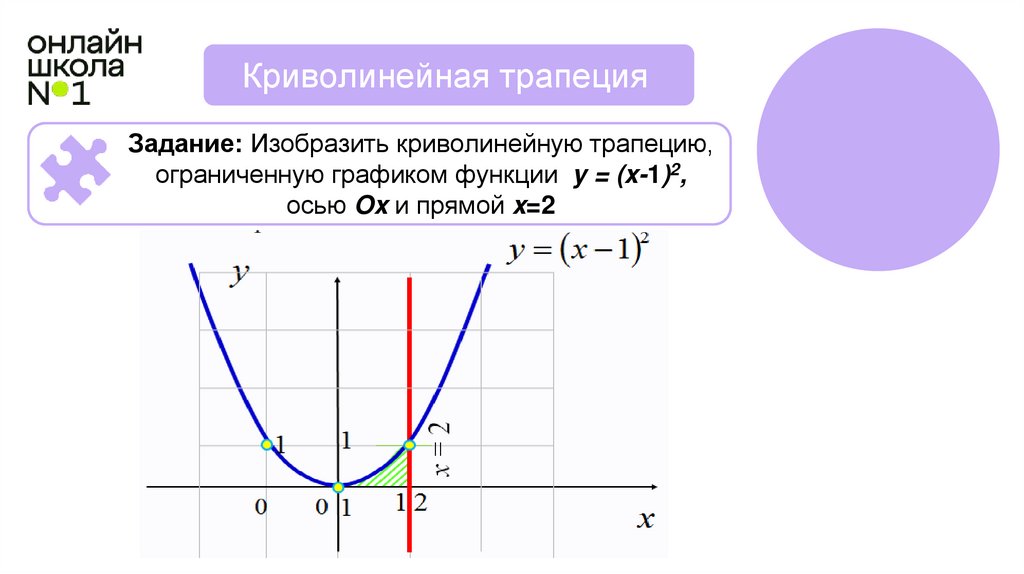
Задание: Изобразить криволинейную трапецию,
ограниченную графиком функции y = (x-1)2,
осью Ox и прямой x=2

8.

Формула площади
криволинейной трапеции
S F (b) F ( a )
где F(x) – любая первообразная функции f(x).

9.

Формула Ньютона-Лейбница
S F (b) F (a)
b
F (b) F (a)
f
(
x
)
dx
a
b
S f ( x)dx
a

10.

Площадь
криволинейной
трапеции
Название
слайда
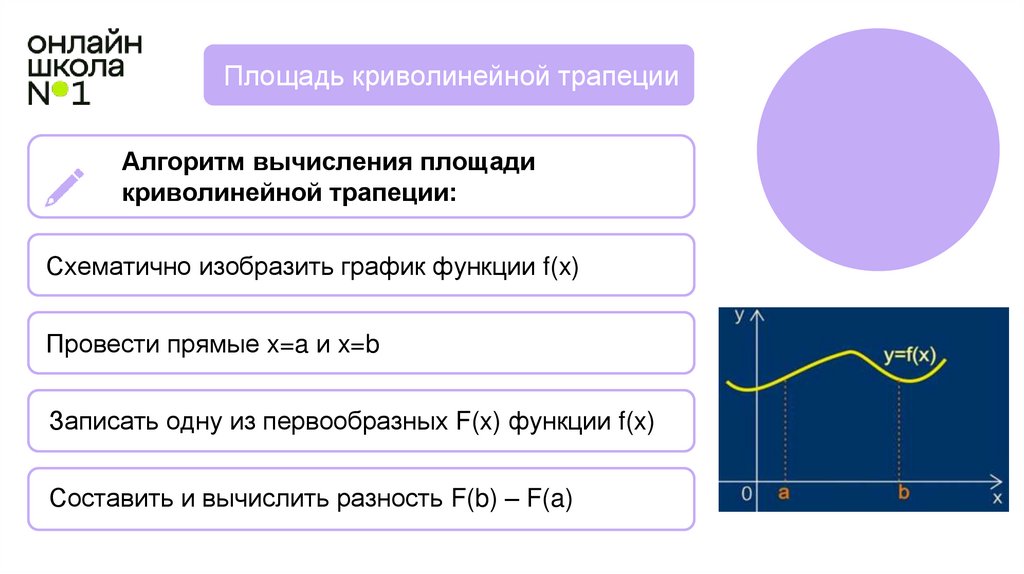
Алгоритм вычисления площади
криволинейной трапеции:
Схематично изобразить график функции f(x)
Провести прямые x=a и x=b
Записать одну из первообразных F(x) функции f(x)
Составить и вычислить разность F(b) – F(a)

11.

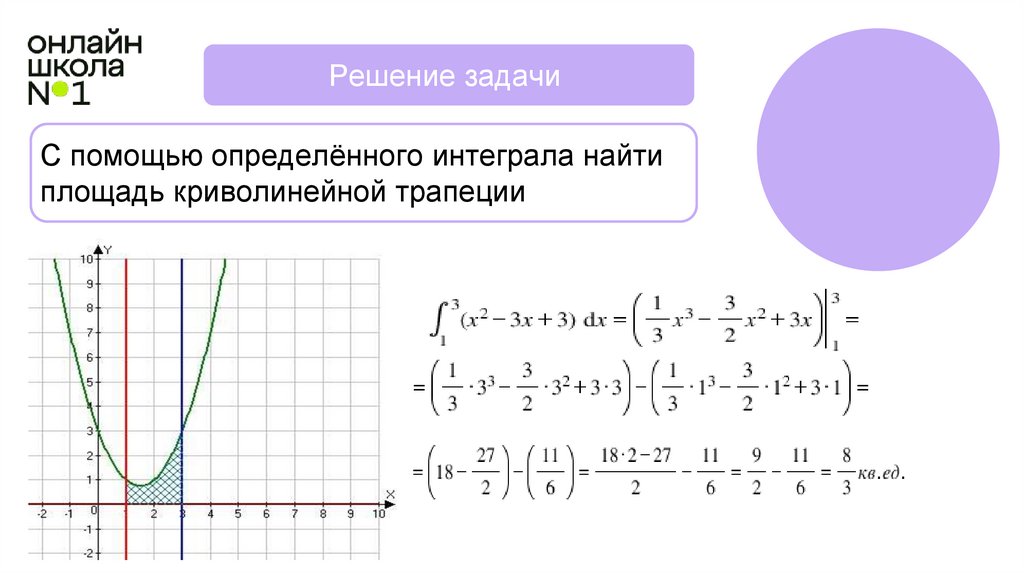
Решение задачи
С помощью определённого интеграла найти
площадь криволинейной трапеции

12.

Закрепление материала
Ответьте на вопросы:
1) Какая трапеция называется криволинейной?
2) С помощью какой формулы находят площадь
криволинейной трапеции?
3) Назовите формулу Ньютона-Лейбница

13.

ПОДВЕДЁМ ИТОГ
ТЕПЕРЬ ВЫ ЗНАЕТЕ:
• Определение «криволинейной
трапеции» и их виды
• Формулы первообразной и
интеграла
• Алгоритм вычисления площади
криволинейной трапеции
ТЕПЕРЬ ВЫ УМЕЕТЕ:
• Находить площадь
криволинейной трапеции с
помощью первообразной
• Вычислять первообразную
функции через интеграл

14.

Спасибо за внимание!
До встречи на следующем уроке!