Похожие презентации:
Решение простейших тригонометрических уравнений
1.
Решение простейшихтригонометрических
уравнений
2.
Уравнение sin х = aа=1,4
y
Число а отмечаем на оси синусов – ось Оу
1
Если а > 1 (а=1,4)
или а < -1 (а = - 1,6)
Нет точек пересечения
с окружностью.
1
о
1
1
Уравнение не имеет решений.
а = - 1,6
x
3.
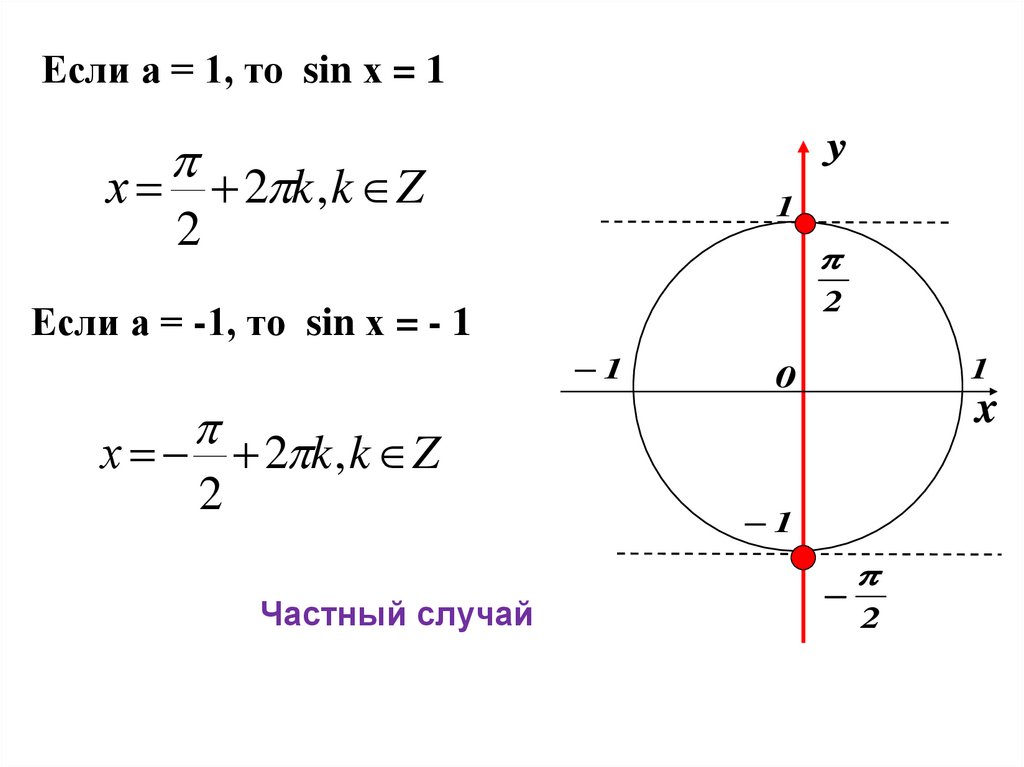
Если а = 1, то sin х = 1y
х 2 k , k Z
2
1
2
Если а = -1, то sin х = - 1
1
х 2 k , k Z
2
Частный случай
1
0
x
1
2
4.
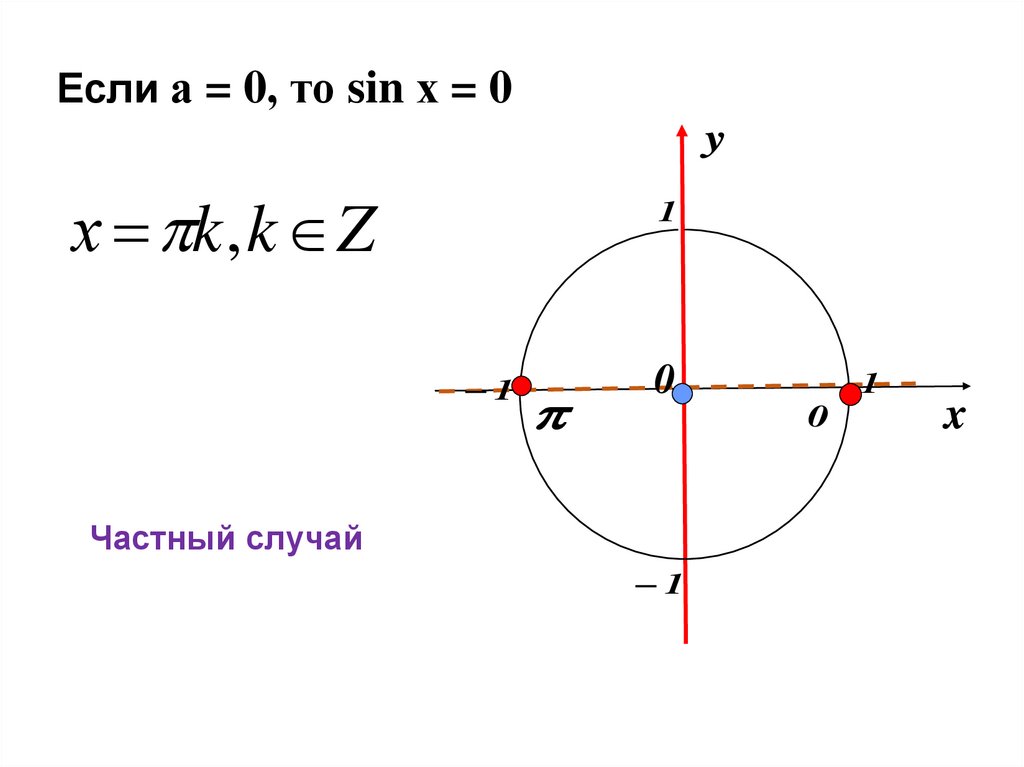
Если а = 0, то sin х = 0y
х k , k Z
1
1
0
1
0
Частный случай
1
x
5.
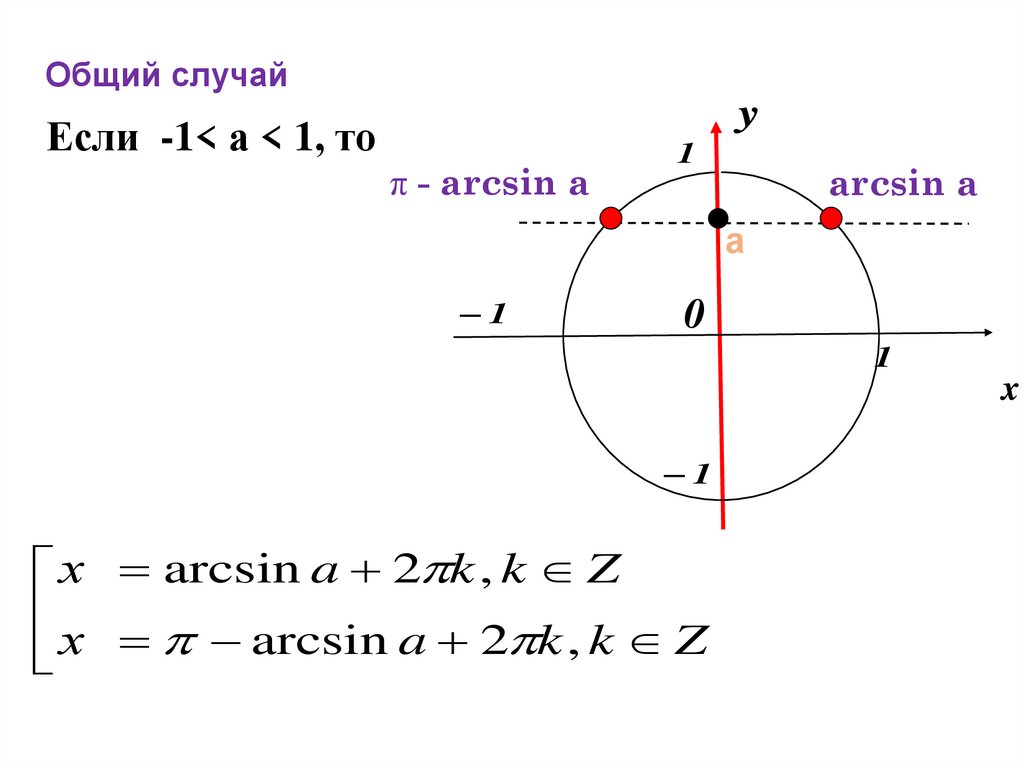
Общий случайЕсли -1< а < 1, то
y
π - arcsin a
1
arcsin а
а
1
а
0
1
x
1
х arcsin a 2 k , k Z
х arcsin a 2 k , k Z
6.
Решение уравнения sin х = aОбщий случай:
-1< а <1
t arcsin a 2 k , k Z
,то
t arcsin a 2 k , k Z
Частный случай:
sin t = 1 , то
t 2 k ,k Z
2
sin t = 0 , то
t k , k Z
sin t = - 1 , то
t 2 k , k Z
2
Если а > 1 или а < -1,то уравнение решений не имеет.
7.
t arcsin a 2 k , k Zt arcsin a 2 k , k Z
1
sin x
2
x
x
x
x
x
x
1
arcsin 2 k ,k Z
2
1
( arcsin ) 2 k ,k Z
2
6
2 k ,k Z
( ) 2 k ,k Z
6
2 k ,k Z
6
5
2 k ,k Z
6
5
Ответ : 2 k ;
2 k , k Z
6
6
8.
sin 4x 0Учащиеся делят обе части на 4
и получают следующее:
sin x 0
Грубая ошибка.
9.
xsin t 1,
sin 1
2
x
2 k , k Z
2 2
x
2
то t
2 2 k 2, k Z
x 4 k , k Z
Ответ : 4 k , k Z
2
2 k , k Z
10.
1sin 4 x
2
t arcsin a 2 k , k Z
t arcsin a 2 k , k Z
1
4 x 6 2 k , k Z
4 x arcsin 2 2 k , k Z
4 x ( arcsin 1 ) 2 k , k Z 4 x ( ) 2 k , k Z
2
6
k
4 x 6 2 k , k Z x 24 2 , k Z
4 x 5 2 k , k Z x 5 k , k Z
6
24 2
k 5 k
Ответ : ,
,k Z
24 2 24 2
11.
t arcsin a 2 k , k Zt arcsin a 2 k , k Z
3
sin( x )
6
2
3
2 k , k Z
x arcsin
2
6
3
) 2 k , k Z
x ( arcsin
2
6
x 6 3 2 k , k Z
x ( ) 2 k , k Z
6
3
x 3 6 2 k , k Z
x 2 2 k , k Z
x 2 2 k , k Z
x 5 2 k , k Z
6
3 6
5
Ответ : 2 k ,
2 k , k Z
2
6
12.
sin x2
2
t arcsin a 2 k , k Z
t arcsin a 2 k , k Z
2
) 2 k , k Z
x arcsin(
arcsin (-a)= - arcsin a
2
2
x ( arcsin( 2 )) 2 k , k Z
2
2 k , k Z
x 2 k , k Z
x arcsin
2
4
2
x ( arcsin 2 ) 2 k , k Z x ( 4 ) 2 k , k Z
x 4 2 k , k Z
x 5 2 k , k Z
4
5
Ответ : 2 k ;
2 k , k Z
4
4
13.
2sin х sin x
sin( x)
2
2
sin x
2
2
sin x
2
2
2
) 2 k , k Z
2 k , k Z
x arcsin(
x arcsin
2
2
2
2
x arcsin( 2 ) 2 k , k Z x arcsin 2 2 k , k Z
x 4 2 k , k Z x 4 2 k , k Z
x 2 k , k Z x 5 2 k , k Z
4
4
5
Ответ : 2 k ;
2 k , k Z .
4
4
14.
Приводим уравнение к стандартному виду:sin х = a
2 sin x 2
sin x 1
2 sin 3x 2
2
sin 3x
2
2 sin 2 x 1 0
2 sin 2 x 1
1
sin 2 x
2
15.
2 sin( x2 sin( x
2 sin( x
sin( x
3
3
3
3
) 1 5
) 5 1
) 4
) 2, т.к. 2 [ 1;1], то
уравнение решений не имеет
Ответ : решений нет.
16.
sin 2x 13
1
sin(
x)
2
2
х
3
sin
5
2
sin 3х 0
2 sin x 2 0
17.
Уравнение cos х = ay
Число а отмечаем на оси косинусов – ось Ох
Если а >1 (а=1,4)
или а < -1 (а = - 1,6)
1
а=1,4
а = - 1,6
Нет точек пересечения
с окружностью
Уравнение не имеет решений
1
о
1
1
x
18.
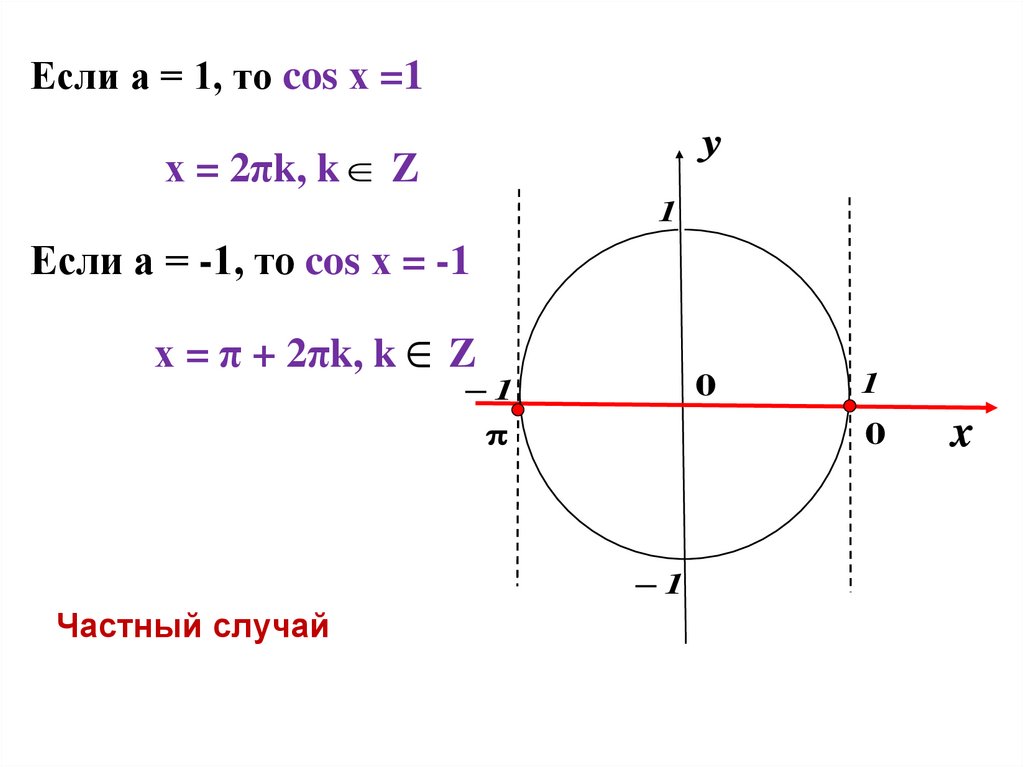
Если а = 1, то cos х =1y
х = 2πk, k Z
1
Если а = -1, то cos х = -1
х = π + 2πk, k Z
1
0
0
1
Частный случай
1
x
19.
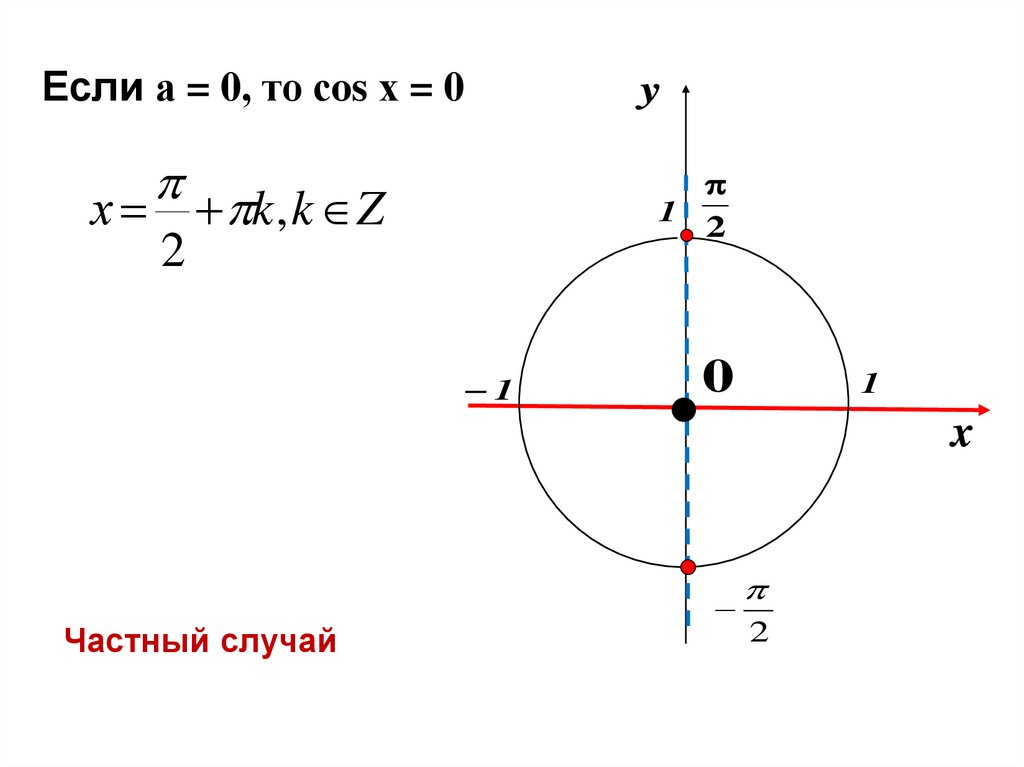
Если а = 0, то сos х = 0y
1
2
х k , k Z
2
1
0
1
x
Частный случай
2
20.
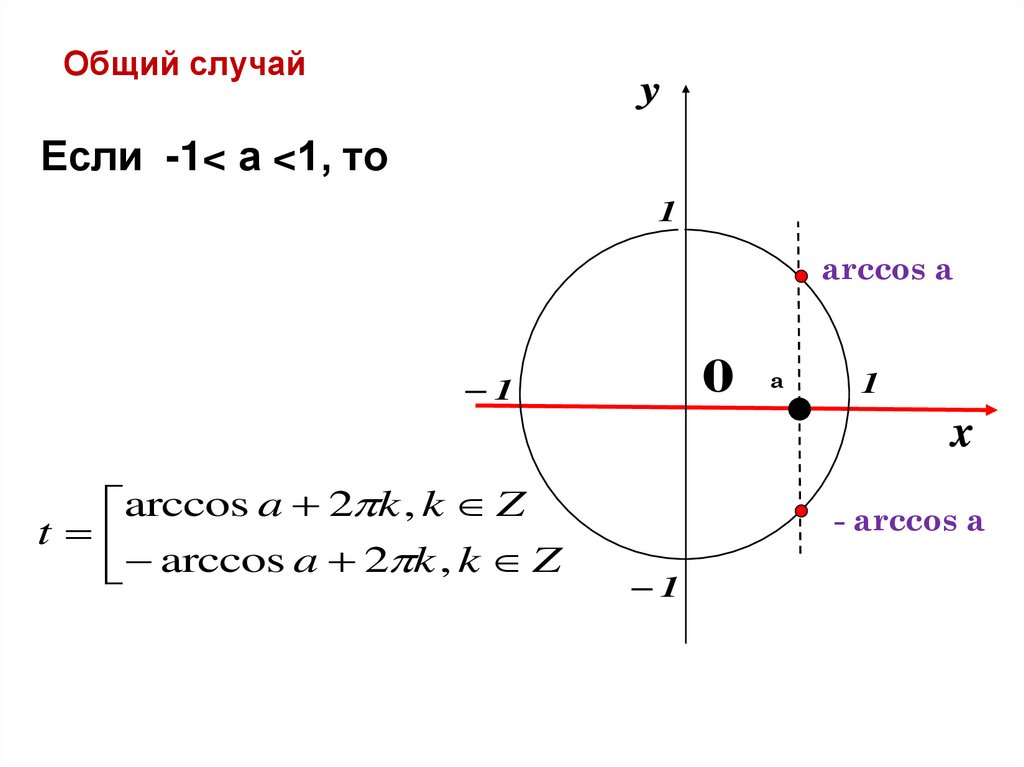
Общий случайy
Если -1< а <1, то
1
arccos а
0
1
а
1
x
arccos a 2 k , k Z
t
arccos a 2 k , k Z
- arccos а
1
21.
Решение уравнения cos х = aОбщий случай:
Частный случай:
t arccos a 2 k , k Z
-1< а <1 ,то
t arccos a 2 k , k Z
cos t = 1 , то
t = 2πk, k Z
cos t = 0 , то
t k , k Z
2
cos t = - 1 , то t = π + 2πk, k Z
Если а 1;1 ,то уравнение решений не имеет.
22.
cos 2 x 12 x 2 k , k Z
2 k
x
,k Z
2
x k , k Z
Ответ : k , k Z
cos( x
x
x
3
) 0
3
2
k , k Z
k , k Z
2 3
3 2
х
k , k Z
6
6
x
6
k , k Z
Ответ :
6
k , k Z
23.
x 1t arccos a 2 k , k Z
cos
t arccos a 2 k , k Z
3 2
1
x
x
arccos
2
k
,
k
Z
2
k
,
k
Z
3
3 3
2
x arccos 1 2 k , k Z x 2 k , k Z
3
3
2
3
x
3
3
2
k
,
k
Z
x 6 k , k Z
3
x 3 3 2 k , k Z x 6 k , k Z
3
Ответ : 6 k ; 6 k , k Z
24.
t arccos a 2 k , k Zt arccos a 2 k , k Z
3
arccos (-a)= π - arccos a
cos х
2
3
3
) 2 k , k Z
х arccos( ) 2 k , k Z х ( arccos
2
2
3
3
) 2 k , k Z
х arccos( ) 2 k , k Z х ( arccos
2
2
5
х ( 6 ) 2 k , k Z х 6 2 k , k Z
х ( ) 2 k , k Z х 5 2 k , k Z
6
6
5
5
Ответ :
2 k ;
2 k , k Z
6
6
25.
2 cos( 5 x) 33
cos( 5 x)
2
3
cos5 x
2
3
3
2 k , k Z
5 x arccos( ) 2 k , k Z 5 x arccos
2
2
3
3
5 x arccos( 2 ) 2 k , k Z 5 x ( arccos 2 ) 2 k , k Z
5
2 k
5 x 6 2 k , k Z 5 x 6 2 k , k Z x 6 5 , k Z
5 x ( ) 2 k , k Z 5 x 5 2 k , k Z x 2 k , k Z
6
6
6
5
2 k 2 k
Ответ :
;
,k Z
6
5
6
5
26.
3 cos( x3 cos( x
3 cos( x
3
3
3
) 2 6
) 6 2
) 8
8
cos( x )
3
3
8
cos( ( x ))
3
3
8
8
cos(x ) , т.к. 1;1 , то
3
3
3
уравнение решений не имеет
Ответ : решений нет.
27.
xcos 0,3
3
x
arccos
0
,
3
2
k
,
k
Z
3
x arccos 0,3 2 k , k Z
3
х 3 аrc cos 0,3 6 k , k Z
х 3 arccos 0,3 6 k , k Z
Ответ : 3 аrc cos 0,3 6 k ; 3 аrc cos 0,3 6 k , k Z
28.
xcos 1
5
2
cos(x )
4
2
1
cos3 x
2
cos 2 x 1 2
cos 2 x 1 2
29.
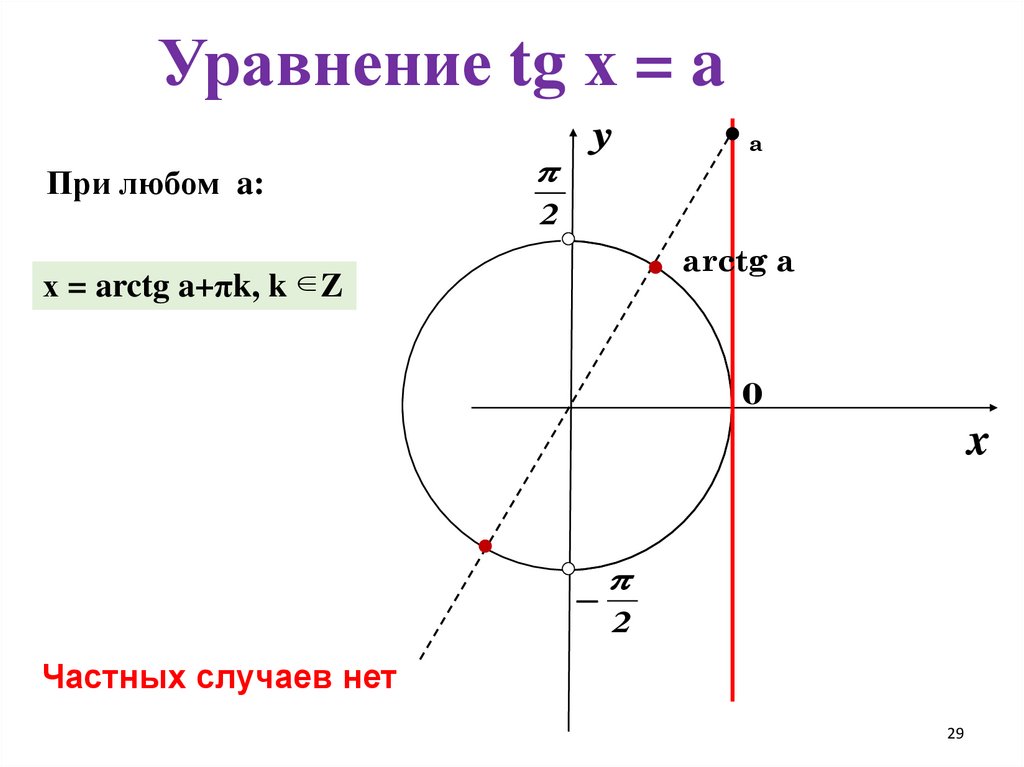
Уравнение tg х = aПри любом a:
y
а
2
arctg a
х = arctg a+πk, k Z
0
x
2
Частных случаев нет
29
30.
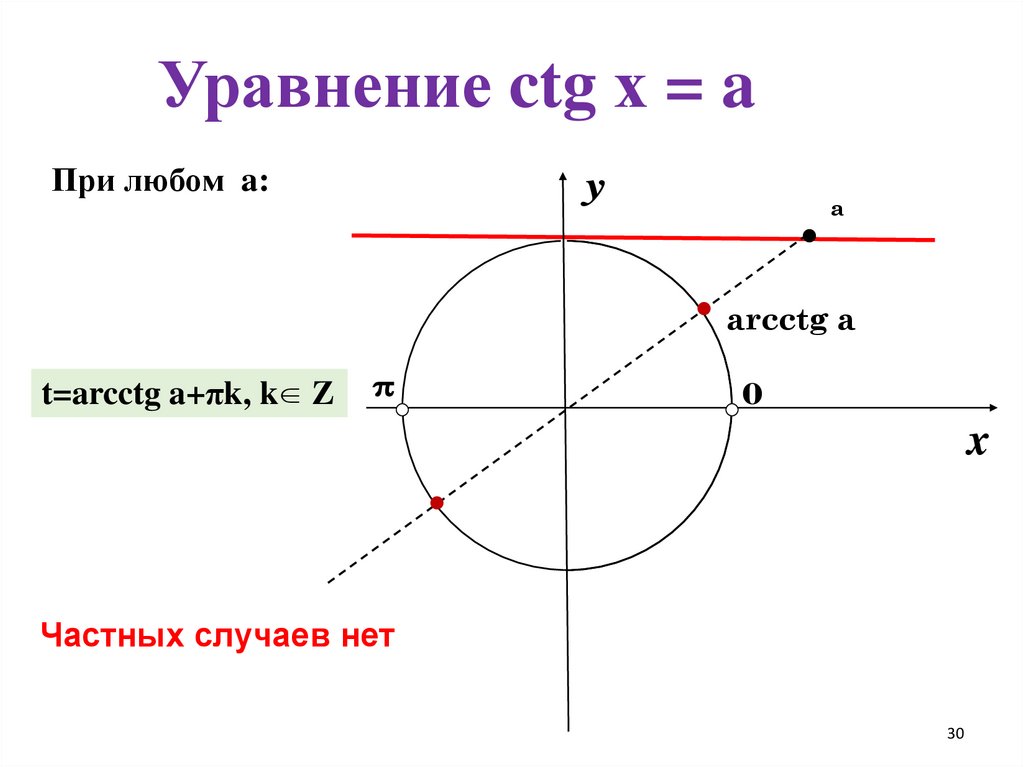
Уравнение ctg х = aПри любом a:
y
а
arcctg a
t=arcctg a+πk, k Z
0
x
Частных случаев нет
30
31.
tgх aсtgх a
х arctga k , k Z
х arcctga k , k Z
tg 2 х 3
2 х arctg 3 k , k Z
2х
х
х
3
k , k Z
3 2
6
k
k
Ответ :
2
6
2
,k Z
,k Z
k
2
,k Z
сtg ( x ) 1
4
x
x
4
4
x
arcctg1 k , k Z
4
k , k Z
k , k Z
4 4
x k , k Z
Ответ : k , k Z
32.
tgх aсtgх a
arctg (-a)= - arctg a
х arctga k , k Z arcctg (-a)= π - arcсtg a х arcctga k , k Z
х
tg 1
5
х
arctg ( 1) k , k Z
5
х
arctg1 k , k Z
5
х
k , k Z
5
4
5
х
5 k , k Z
4
5
Ответ :
5 k , k Z
4
1
сtg ( x )
3
3
1
x arcctg (
) k , k Z
3
3
1
x arcctg
k , k Z
3
3
x
3
3
k , k Z
2
x
k , k Z
3
3
2
x
k , k Z
3 3
x k , k Z
Ответ : k , k Z
33.
tgt at arctga k , k Z
сtgt a
t arcctga k , k Z
tg (-a)= - tg a
2tg ( х) 3
2tgх 3
3
tgx
2
3
х arctg ( ) k , k Z
2
3
х arctg k , k Z
2
3
Ответ : arctg k , k Z
2
x
3
4
x
3
ctg
4
3
x
3
arcctg (
) k , k Z
4
3
x
arcctg 3 k , k Z
4
x
k , k Z
4
6
x 5
k , k Z
4
6
20
x
4 k , k Z
6
10
Ответ :
4 k , k Z
3
3ctg
34.
1cos 3x
3
2
2
cos 2x
2
2
3
sin 4x
0
2
2 cos x 0
cos( x) 1
2 cos 4x 1 0
x
3ctg 3
2
x
3tg 1
3
3tg 4 x 3 0


















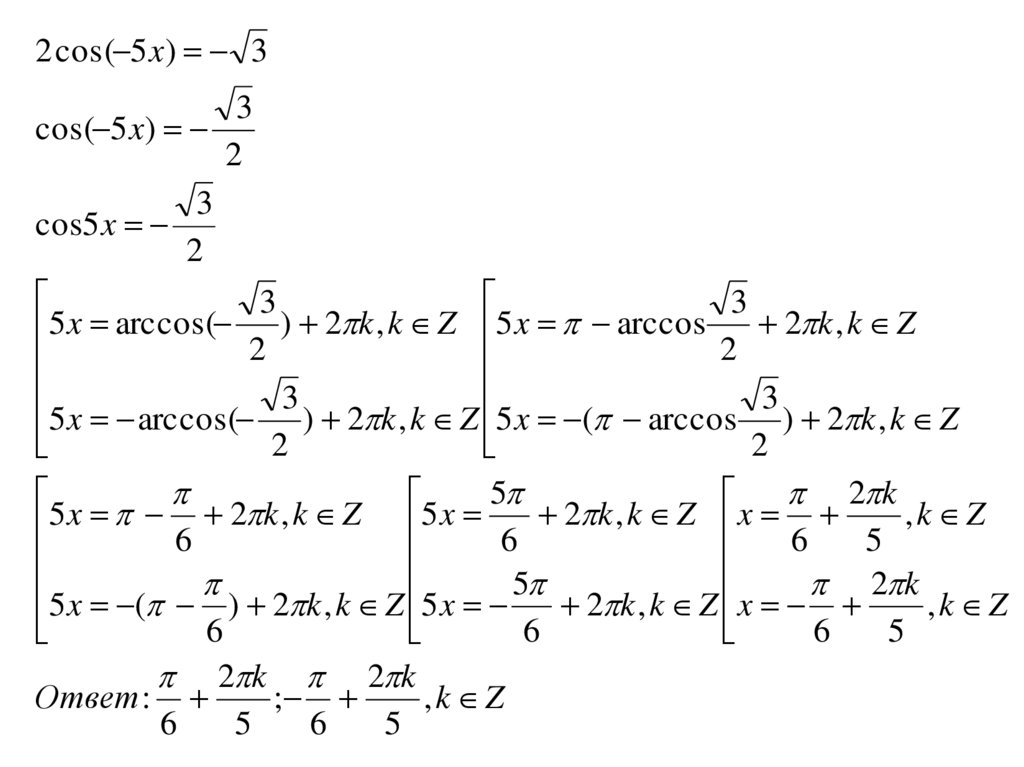


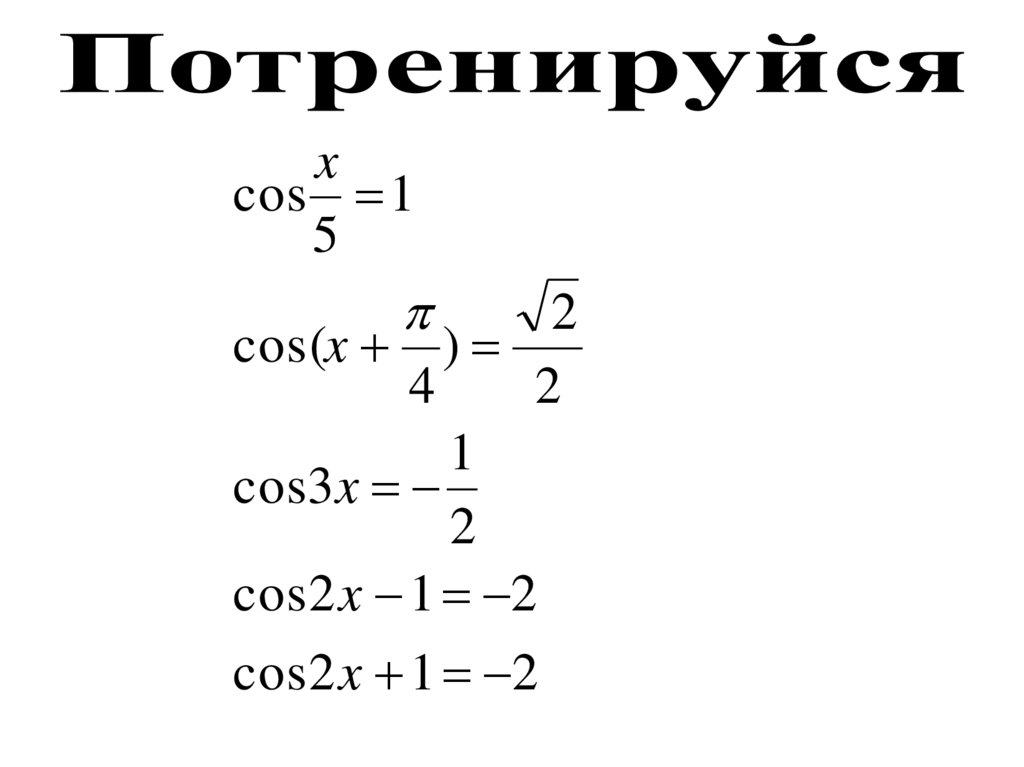



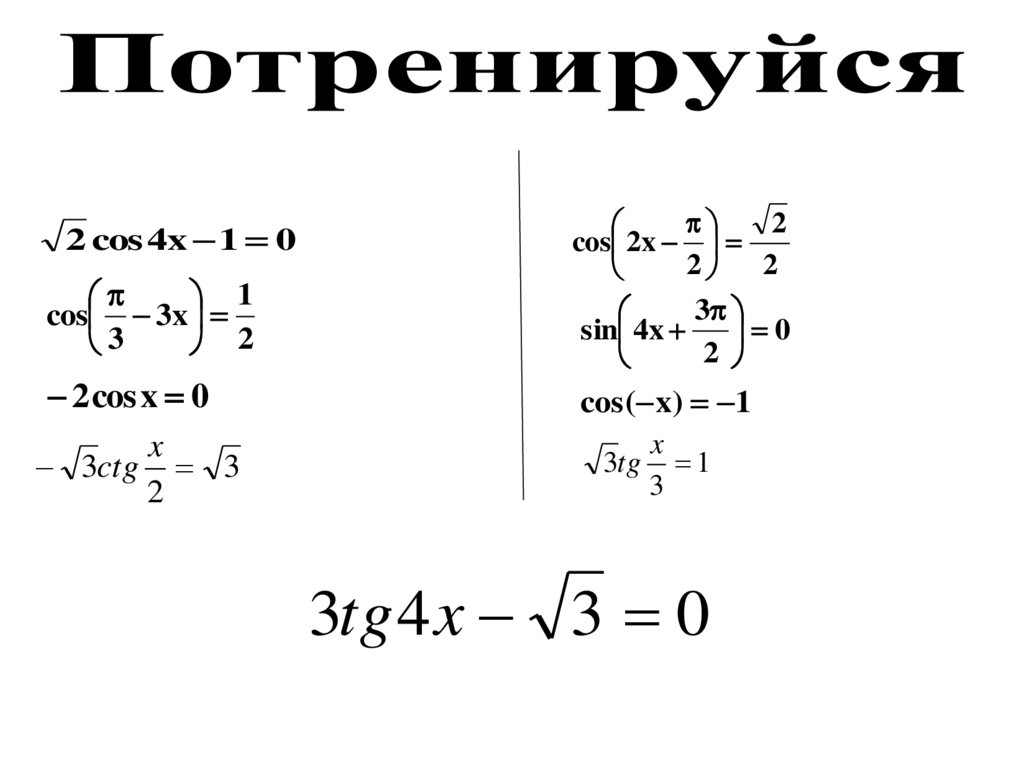
 Математика
Математика








