Простейшие тригонометрические уравнения

1. Простейшие тригонометрические уравнения.

2.

Арккосинусом числа а называют такое число из
промежутка [0;π], косинус которого равен а
arccos?a У
С
D
a
arccos a
B
a
А
Х
Область определения:
1 a 1
Область значений:
0 arccos a
Свойство:
? АС АD СD АD AB arccos a
arccos( a ) arccos a

3.

Арксинусом числа а называют такое число из
промежутка [-π/2;π/2], синус которого равен а
У
a
arcsin a
B
А
a
Область определения:
1 a 1
Х
Область значений:
arcsin a
С ? arcsin a
2
2
Свойство:
АВ СА ? arcsin a
arcsin( a ) arcsin a

4.

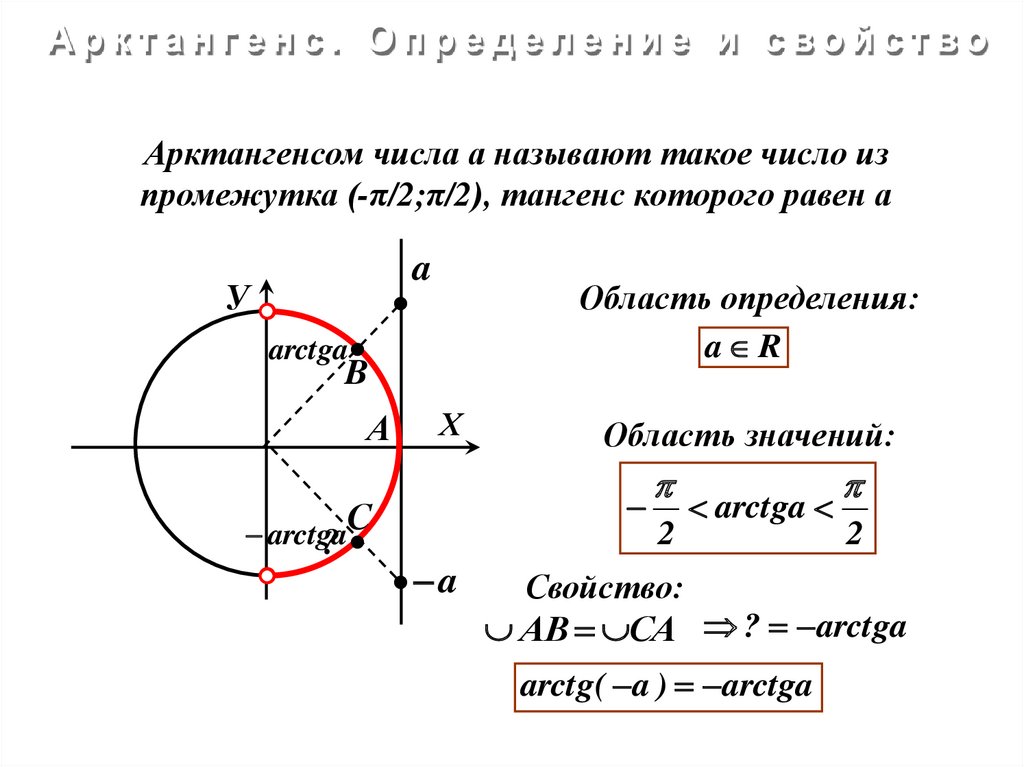
Арктангенсом числа а называют такое число из
промежутка (-π/2;π/2), тангенс которого равен а
a
У
Область определения:
a R
arctga
B
А
С
arctga
?
Х
a
Область значений:
arctga
2
2
Свойство:
АВ СА ? arctga
arctg( a ) arctga

5.

Арккотангенсом числа а называют такое число из
промежутка (0;π), котангенс которого равен а
a
a
У
arcctga
?
D
С
B arcctga
А
Х
Область определения:
a R
Область значений:
0 arcctga
Свойство:
? АС АD СD АD AB arcctga
arcctg ( a ) arcctga

6.

У
cos t a
arccos a
a 2 k
Ответ: tt arccos
или
arccos a 2 k
t
arccos a 2 k
k Z
Точки, симметричные
относительно Ох могут
быть записаны в виде…
a
0
Х
arccos a

7.

У
sin t a
arcsin a
a
arcina
0
k a 2 k
Ответ: tt (arcsin
1
)
arcsin a k
или
t arcsin a 2 k
k Z
Точки, симметричные
относительно Оу могут
быть записаны в виде…
Х

8.

tgt 1,5
Y
1,5
Ответ:
t arctg 1,5 k
arctg 1,5
k Z
X

9.

сtgt 2
Y
2
arcctg ( 2 )
X
Ответ:
( 22) kk
или
tt arcctg
arcctg
k Z

10.

Наша задача: привести уравнение к
простейшему виду

11.

x 1
Пример 1. Решить уравнение sin
4 2
x
Решение: Введем новую переменную t
4
Уравнение уже
является
простейшим
Тогда уравнение примет вид
t1
6
1
sin t
2
2 n, n Z
5
t2
2 n, n Z
6
Возвращаемся к переменной х
x1
2 n, Z
4 6
x2 5
4
6
Со временем, при
наличии опыта,
2 n,промежуточную
Z
переменную можно не
вводить
Осталось умножить обе части каждого равенства на 4
2
x1
8 n, Z
3
10
x2
8 n, Z
3

12.

Пример 2. Решить уравнение
cos 4x 0
Решение: Мы знаем, что решения
уравнения cos t 0
имеют вид
t
2
n, n Z
Для данного примера это означает, что
4x
2
n, n Z
Разделим обе части этого равенства на 4
x
Ответ:
8
8
n
4
n
4
,n Z
,n Z
Уравнение является
простейшим. Применяем
формулу для частного
случая

13.

Пример 3. Решить уравнение 2 cos
3x 2
4
Решение: Приведем уравнение к стандартному виду. Для этого
разделим обе части равенства на 2.
Воспользуемся тем,
что cos t cos t
2
cos 3x
4
2
2
cos 3x
4 2
3x
3x
4
4
3x
arccos
4
4
4
Решениями уравнения
Являются числа видв
2
2 n, n Z
2
cos t a
t arccos a 2 n, n Z
2 n, n Z
2 n, n Z
2 n
x
,n Z
12 12
3

14. Домашнее задание

№22.18 а)б)
№22.19 а)
№22.20 б)
№22.21 б)