Матрицы и определители

1. Тема: «МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ»

Вопросы:
1. Понятие матрицы
2. Операции над матрицами
3. Определители второго и третьего порядков,
их
свойства
4. Понятие определителя n-го порядка
5. Ранг матрицы
6. Обратная матрица
7. Собственные числа и собственные векторы матриц

2. 1. Понятие матрицы

Матрицей называется прямоугольная таблица чисел,
содержащая m строк одинаковой длинны (или n столбцов
одинаковой длинны). Матрица записывается в виде
а11 а12
а21 а22
А
...
...
а
m1 аm 2
... а1n
... а2 n
... ...
... аmn
или, сокращённо, А аij , где i 1, m строки, j 1, n - номер столбца.
номер

3.

Матрицу А называют матрицей размера m×n и
пишут Am×n. Числа aij, составляющие матрицу,
называются её элементами.
Матрицы равны между собой, если равны все
соответствующие элементы этих матриц, т. е. A=B, если
aij= bij.
Диагональная матрица, у которой каждый элемент
главной диагонали равен единице, называется
единичной.
Е3 3
1 0 0
0 1 0
0 0 1

4.

Матрица, содержащая один столбец или одну
строку, называется вектором (или вектор-столбец, или
вектор-строка, соответственно).
а1
а2
А
а
m
В b1 b2 bn
Матрица, полученная из данной заменой каждой её
строки столбцом с тем же номером, называется матрицей
транспонированной к данной. Обозначается АТ.
Так, если
1 2
,
А
3 4
то
1 3
А
2 4
Т
.

5. 2. Операции над матрицами

Суммой (разностью) двух матриц Аm×n и Вm×n
называется матрица Сm×n такая, что сij = аij + bij
(сij = аij – bij ), (i = 1, 2, ..., m; j = 1, 2, ..., n). Сумма
( разность) матриц А и В обозначается А + В ( А – В).
Произведением матрицы Аm×n на число α называется
матрица Вm×n такая, что bij = αaij и обозначается αА.
Матрица –А называется противоположной А.
Произведением матрицы Аm×n
называется матрица Сm×k такая, что
на матрицу Вn×k
n
cij aisbsj .
s 1

6.

Получение элемента сij схематично изображается так:
i
k
Справедливо: A∙E=E∙A=A, где А – квадратная матрица,
Е – единичная матрица того же размера.
а11 а12
а21 а22
b11 b12
а13
b21 b22
а23
b
b
31 32
a11b11 a12b21 a13b31 a11b12 a12b22 a13b32
a21b11 a22b21 a23b31 a21b12 a22b22 a23b32

7.

Операции сложения матриц и умножения матрицы
на число обладают следующими свойствами:
1. A+B=B+A;
2. A+(B+C)=(A+B)+C;
3. A+O=A;
4. A-A=O;
5. 1∙A=A;
6. α∙(A+B)=αA+αB;
7. (α+β)∙A=αA+βA;
8. α∙(βA)=(αβ)∙A,
где А, В, С – матрицы, α и β – числа.

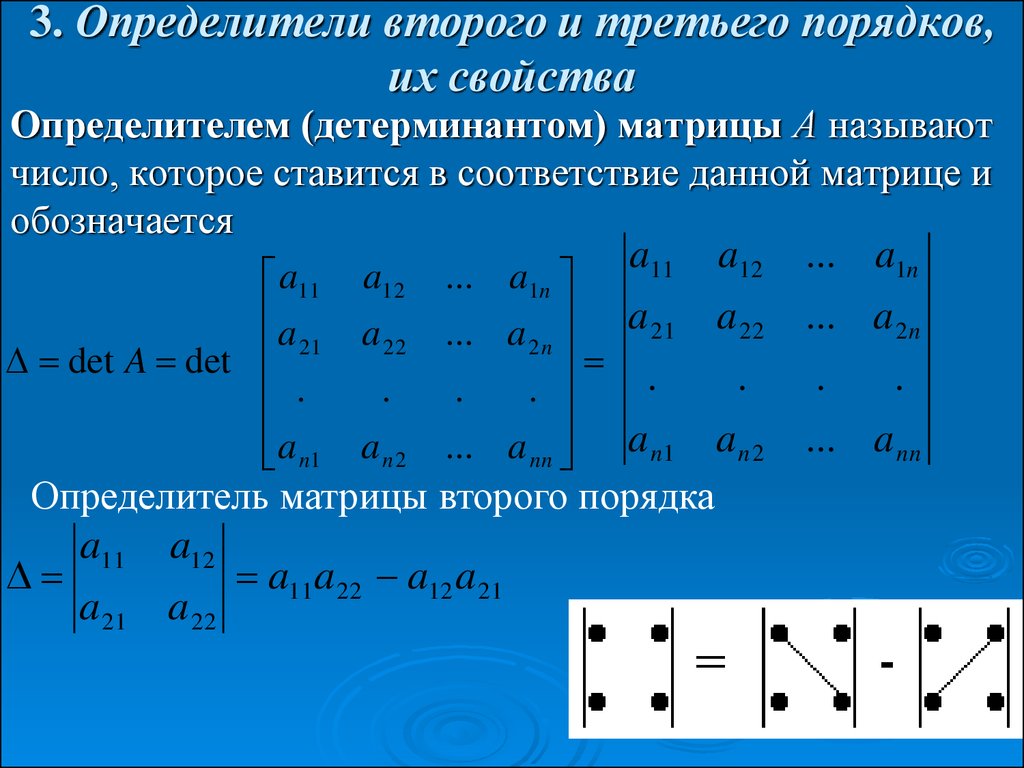
8. 3. Определители второго и третьего порядков, их свойства

Определителем (детерминантом) матрицы А называют
число, которое ставится в соответствие данной матрице и
обозначается
a11 a12 ... a1n
a11
a
det A det 21
.
a n1
a12
a 22
.
an2
... a1n
... a 2 n a 21
.
.
.
a
... a nn
n1
Определитель матрицы второго порядка
a11 a12
a11a 22 a12 a 21
a 21 a 22
a 22
... a 2 n
.
.
.
... a nn
an2

9.

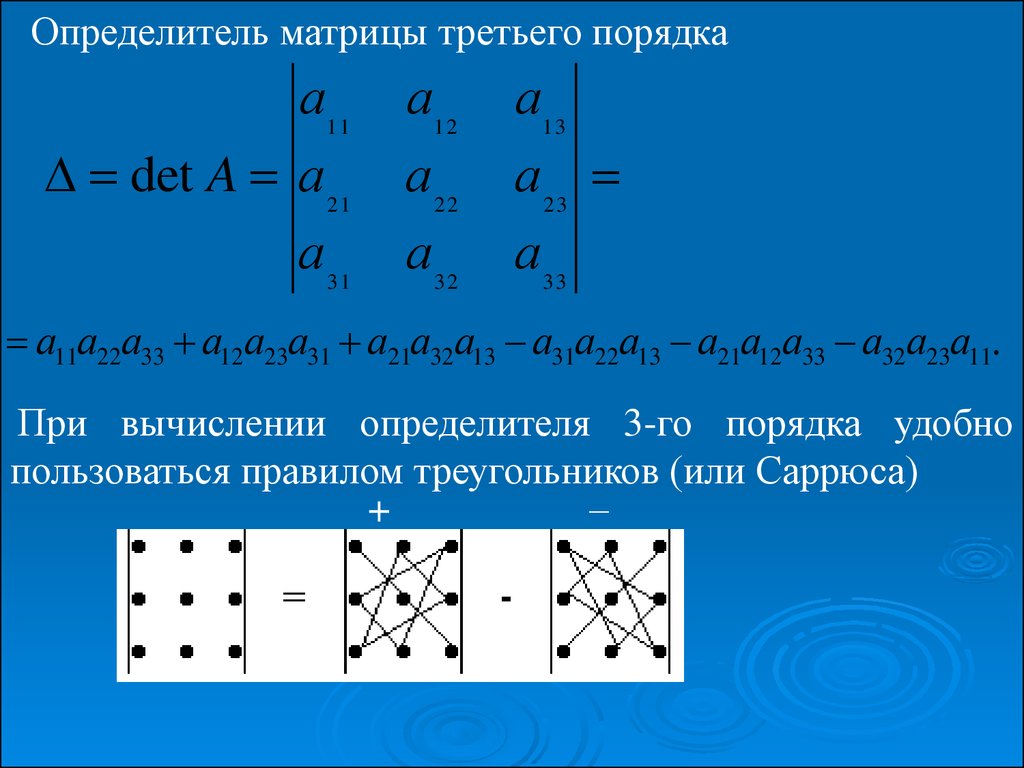
Определитель матрицы третьего порядка
а11
det A а 21
а12
а 22
а13
а 23
а 31
а 32
а 33
а11а22а33 а12а23а31 а21а32а13 а31а22а13 а21а12а33 а32а23а11.
При вычислении определителя 3-го порядка удобно
пользоваться правилом треугольников (или Саррюса)
+
–

10.

Минором элемента аij определителя
n-го порядка
называется определитель n-1-го порядка, полученный из
исходного путём вычёркивания строки и столбца, на
пересечении которых находится выбранный элемент.
Алгебраическим дополнением Аij элемента aij
называется минор этого элемента, умноженный на (–1)i+j
Ai j = (–1)i+ j Mi j.
Т. Сумма произведений элементов какой-нибудь строки
(столбца) на их алгебраические дополнения равна
определителю матрицы.

11.

4. Понятие определителя n-го порядка
Определителем n-го порядка квадратной матрицы А
называется
алгебраическая
сумма
n!-слагаемых
(n! = 1 ∙2∙…·n) вида, a1 1 a2 2 ...an n состоящих из n
сомножителей, взятых по одному из каждой строки и из
каждого столбца. При этом слагаемые, у которых вторые
индексы сомножителей образуют четную перестановку,
берутся со знаком «+», нечетную перестановку – со знаком
«–».
( 1) a1 1 a2 2 ...an n
t

12.

5. Ранг матрицы
Рангом матрицы rА называется наибольший из порядков
ее миноров, отличных от нуля.
Если все миноры матрицы равны нулю, то ранг матрицы
считается равным нулю.
Если ранг квадратной матрицы А порядка n равен r, то
n – r называют дефектом матрицы А. Если А –
невырожденная (det A ≠ 0), то r = n и дефект матрицы А
равен нулю.

13.

6. Обратная матрица
Матрица называется невырожденной, если ее
определитель отличен от нуля.
Матрица А-1 называется обратной квадратной матрице А,
если АА-1= = А-1А = Е.
Теорема. Для того, чтобы обратная матрица к А,
существовала, необходимо и достаточно, чтобы А была
невырожденной.
Теорема. Для невырожденной матрицы существует
единственная обратная матрица.
A11 A21 ... An1
A
A
...
A
1 12
22
n2
1
A
.
.
.
det A .
A1n A2 n ... Ann

14.

7. Собственные числа и собственные векторы матриц
Всякий ненулевой вектор-столбец х , называется
собственным вектором квадратной матрицы А, если
найдется такое число λ, что будет выполняться равенство
Ах х или (А - λ Е) х = 0
Характеристическим уравнением матрицы А, а его
корни
–
характеристическими числами или
собственными значениями матрицы А
a11
A - E
a 21
...
a n1
a12
...
a1n
a 22 ...
...
...
a 2n
...
an2
... a nn
0.