Гомотетия. Подобие фигур

1.

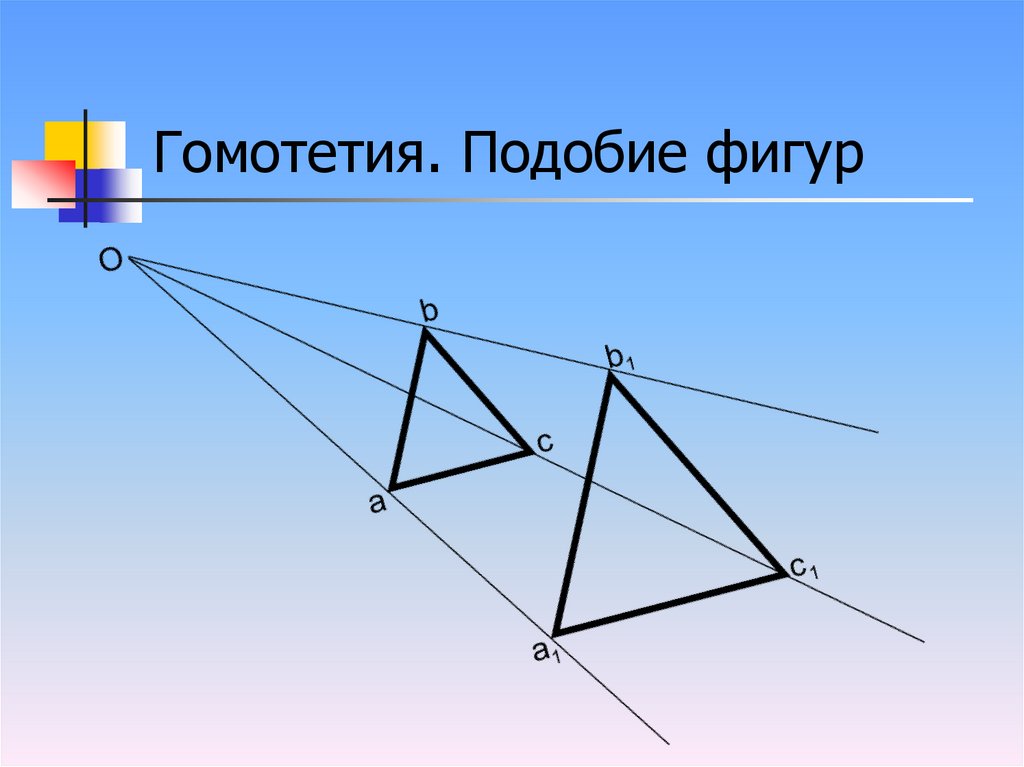
Гомотетия. Подобие фигур

2.

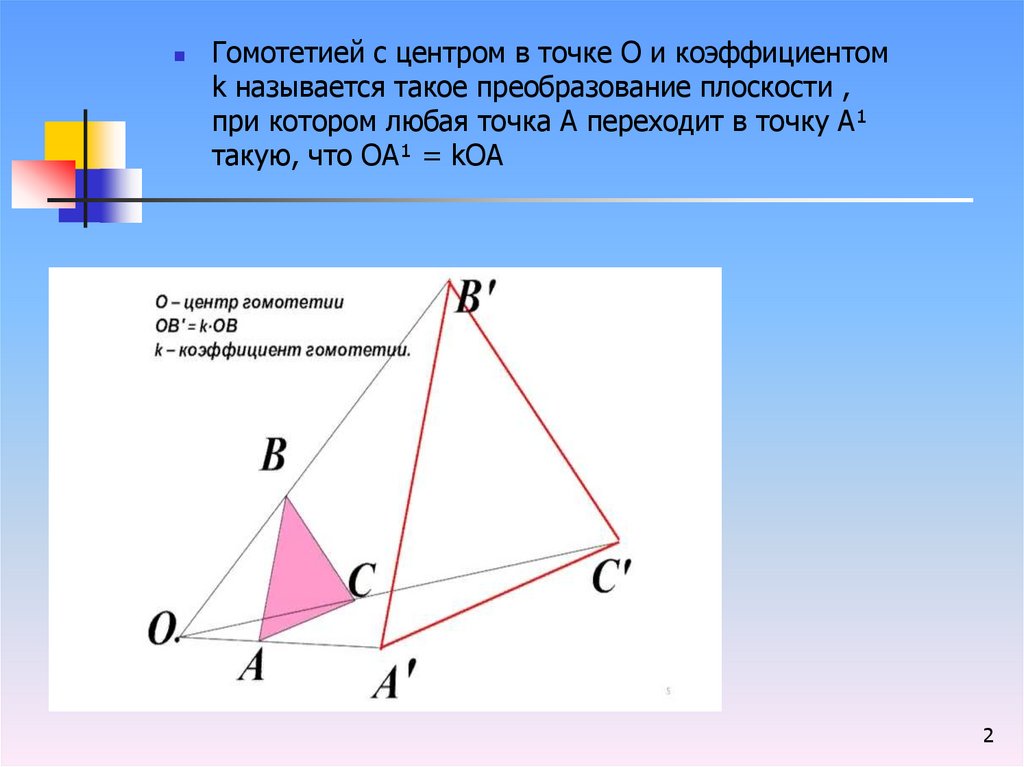
Гомотетией с центром в точке О и коэффициентом
k называется такое преобразование плоскости ,
при котором любая точка А переходит в точку А¹
такую, что ОА¹ = kOA
2

3.

Как построить гомотетичную
фигуру
Построим треугольник А1В1С1,
гомотетичный данному треугольнику abc,
с коэффициентом гомотетии:
k=2
Центр гомотетии - точка O.
3

4.

Шаг 1
Проведём прямые через вершины треугольника и точку О.
4

5.

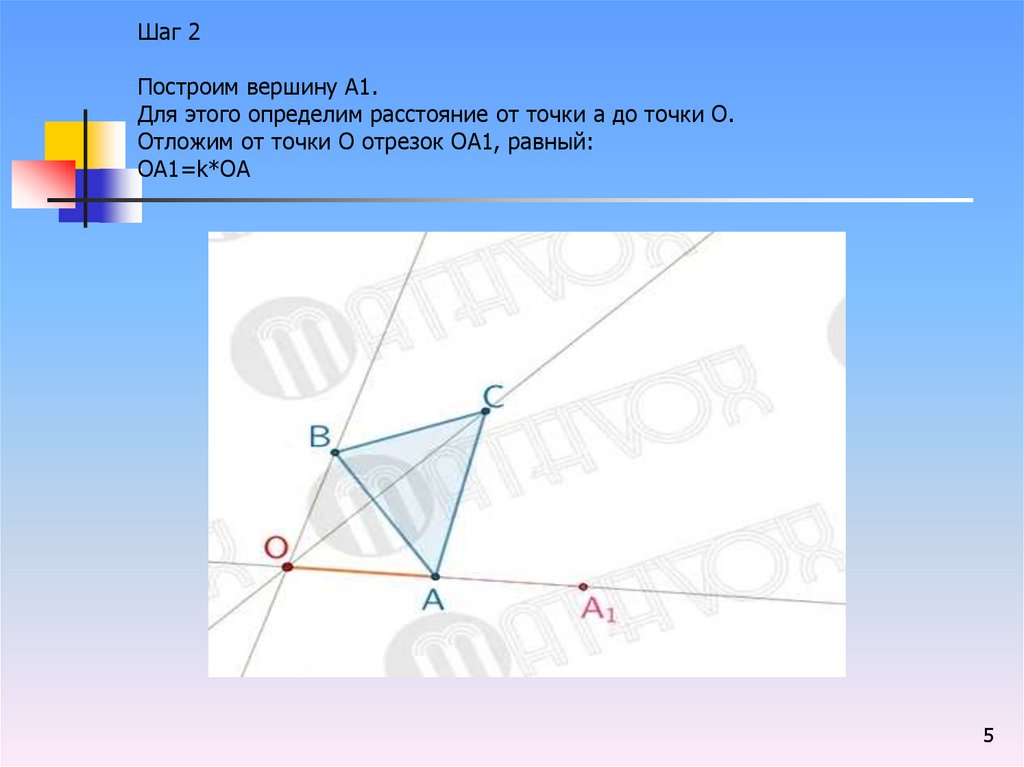
Шаг 2
Построим вершину А1.
Для этого определим расстояние от точки а до точки О.
Отложим от точки О отрезок ОА1, равный:
ОА1=k*ОА
5

6.

Шаг 3
Построим вершину В1, аналогично тому, как мы построили вершину А1.
Для этого определим расстояние от точки В до точки О.
Отложим от точки О отрезок ОВ1, равный:
ОВ1=k*ОВ
6

7.

Шаг 4
Построим вершину С1 аналогично тому, как мы построили вершины А1 и В1:
ОС1=k*OC
7

8.

Шаг 5
Соединим вершины А1,В1,С1.
Таким образом, построили треугольник А1В1С1, который является
гомотетичным треугольнику АВС.
8

9.

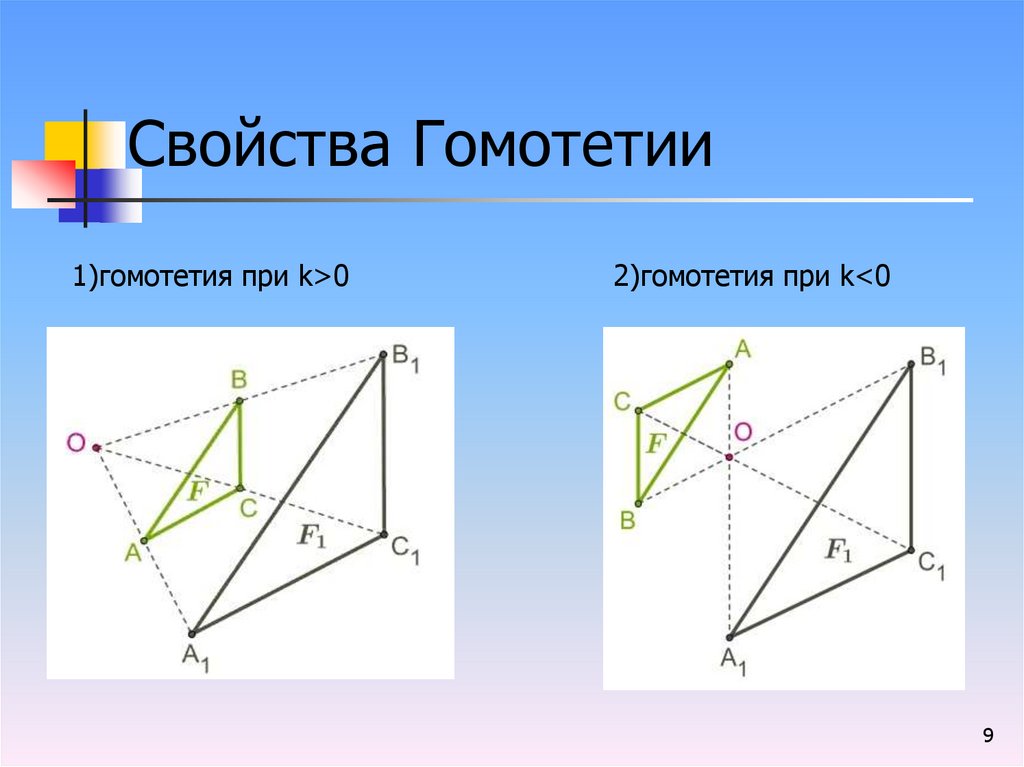
Свойства Гомотетии
1)гомотетия при k>0
2)гомотетия при k<0
9

10.

Свойства Гомотетии
3)гомотетия при k = -1 - это центральная 4)гомотетия при k = 1 - это
симметрия или поворот на 180 градусов тождественное преобразование
5)Прямая переходит в прямую, отрезок в отрезок, угол - в равный ему угол,
окружность - в окружность.
6)Гомотетия является преобразованием
подобия.
10

11.

Отношение площадей подобных многоугольников равно
квадрату коэффициента подобия.
Отношение периметров подобных многоугольников равно
коэффициенту подобия
11

12.

Преобразование подобия в
real life
12