Похожие презентации:
Построение и свойства гомотетии
1. Гомотетия
Подготовила: Карсанова Саидаученица 9 Б класса МОУ СОШ №5
2. Гомотетия с коэффициентом k > 0
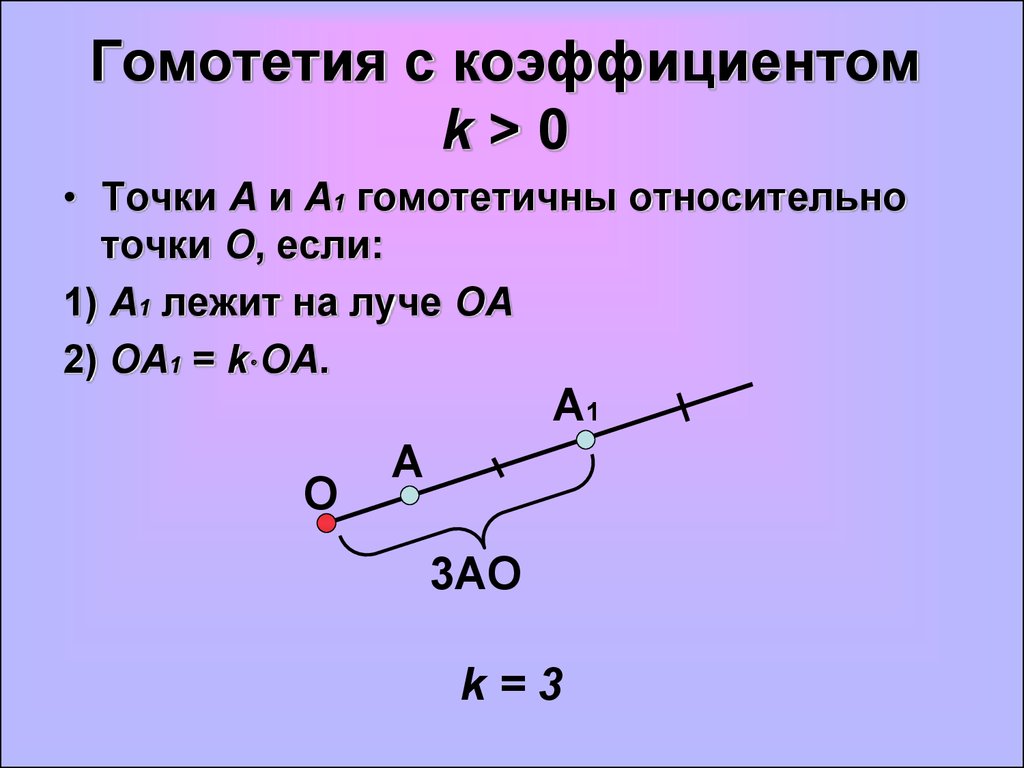
Гомотетия с коэффициентомk>0
• Точки A и А1 гомотетичны относительно
точки О, если:
1) А1 лежит на луче ОА
2) ОА1 = k ОА.
А1
О
А
3АО
k=3
3. Построение гомотетии с коэффициентом k = 1/4
ОВ1
В
1
ОВ
4
4. Построение гомотетии.
yky1
ky2
y1
y2
x
x1 x2
kx1
kx2
5.
• Из определения гомотетии следует, чтопри k = 1 гомотетия является
тождественным преобразованием.
• При k = –1 гомотетия
центральной симметрией.
становится
• Две гомотетии с центром в O и
коэффициентами k и 1/k являются
взаимно обратными. Это означает, что
если одна из них переводит точку A в
точку A1, то другая переводит A1 в A.
6. Свойства гомотетии с коэффициентом k.
• Прямая переходит в параллельную прямую.• Угол переходит в равный ему угол.
• Отрезок переходит в отрезок.
Длины всех отрезков изменяются в k раз.
7. A => A1 B => B1 C => C1 ABC => A1B1C1
A => A1 B => B1 C => C1ABC => A1B1C1
А1
В1
А
В
О
С
С1
8. Задача:
Дано: OMPПостроить: квадрат ABCD, A OM, B MP, C OP, D OP
Решение:
1) Строим квадрат A1B1C1D1:
A1 OM, C1 OP, D1 OP
2) OB1 ∩ MP = B
M
3) BC OP, BA || OP, AD OP
A
4) ABCD – искомый квадрат
A1
O
D1
B
B1
C1
D
C
P







 Математика
Математика








