Теорема о сумме углов треугольника

1.

Теорема о сумме углов
треугольника

2.

180°
Блез Паскаль – французский мыслитель,
математик и физик XVII века

3.

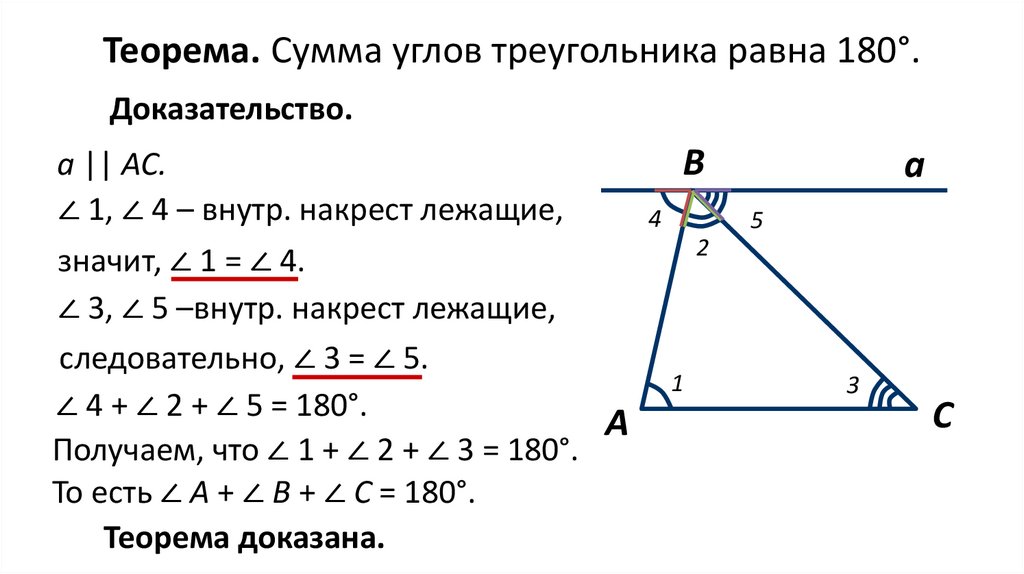
Теорема. Сумма углов треугольника равна 180°.
Доказательство.
а || АС.
∠ 1, ∠ 4 – внутр. накрест лежащие,
значит, ∠ 1 = ∠ 4.
∠ 3, ∠ 5 –внутр. накрест лежащие,
следовательно, ∠ 3 = ∠ 5.
∠ 4 + ∠ 2 + ∠ 5 = 180°.
А
Получаем, что ∠ 1 + ∠ 2 + ∠ 3 = 180°.
То есть ∠ А + ∠ В + ∠ С = 180°.
Теорема доказана.
В
4
а
5
2
1
3
С

4.

Углы равностороннего треугольника равны по 60°.
60°
60°
60°

5.

Сумма острых углов прямоугольного треугольника
равна 90°.
1
2
∠ 1 + ∠ 2 = 90°

6.

Внешним углом треугольника называют угол, смежный
с каким-либо углом треугольника.
В
1
А
2
С

7.

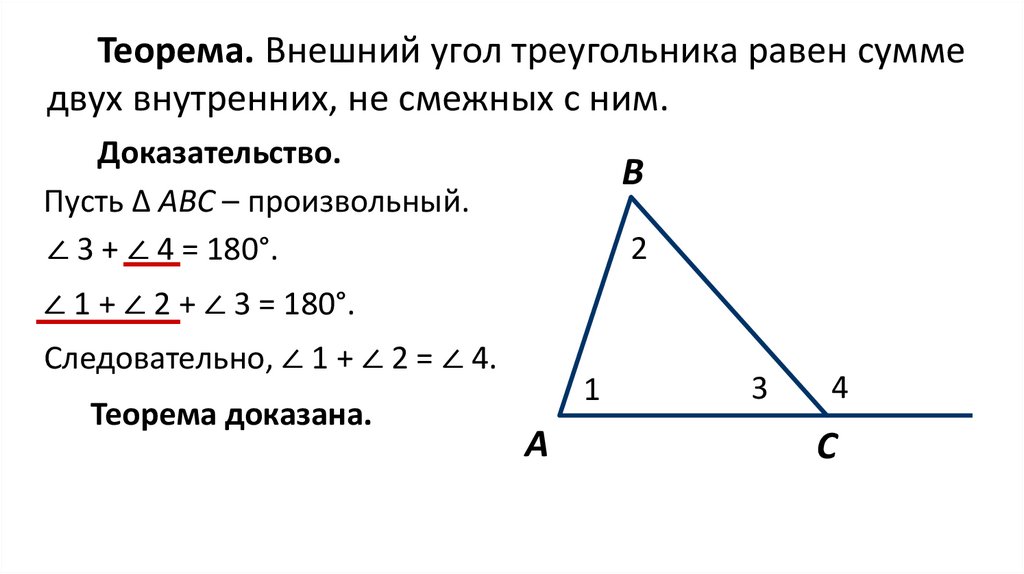
Теорема. Внешний угол треугольника равен сумме
двух внутренних, не смежных с ним.
Доказательство.
Пусть ∆ АВС – произвольный.
∠ 3 + ∠ 4 = 180°.
В
2
∠ 1 + ∠ 2 + ∠ 3 = 180°.
Следовательно, ∠ 1 + ∠ 2 = ∠ 4.
Теорема доказана.
1
А
3
4
С

8.

Задача. Стороны АВ и ВС треугольника АВС равны.
Угол А равен 42°. Чему равна градусная мера угла В?
Решение.
Так как АВ = ВС,
то ∆ АВС – равнобедренный.
Значит, ∠ С = 42°.
∠ А + ∠ В + ∠ С = 180°,
∠ В = 180° – ∠ А – ∠ С,
∠ В = 180° – ∠ 42° – ∠ 42°,
∠ В = 96°.
Ответ: 96°.
В
42°
А
С

9.

Задача. На рисунке ∠ ВСD равен 110°, а ∠ ВАС равен
45°. Найдите градусную меру ∠ АВЕ.
Решение.
Так как ∠ BCD, ∠ BCA – смежные,
то ∠ BCD + ∠ BCA = 180°.
Тогда ∠ BCА = 180° – 110° = 70° .
∠ АBЕ – внешний, смежный с ∠ АBС,
значит, ∠ АBЕ = ∠ ВАС + ∠ АСВ.
Следовательно, ∠ АBЕ = 45° + 70°, А
∠ АBЕ = 115°.
Ответ: 115°.
Е
45°
В
110°
С
D

10.

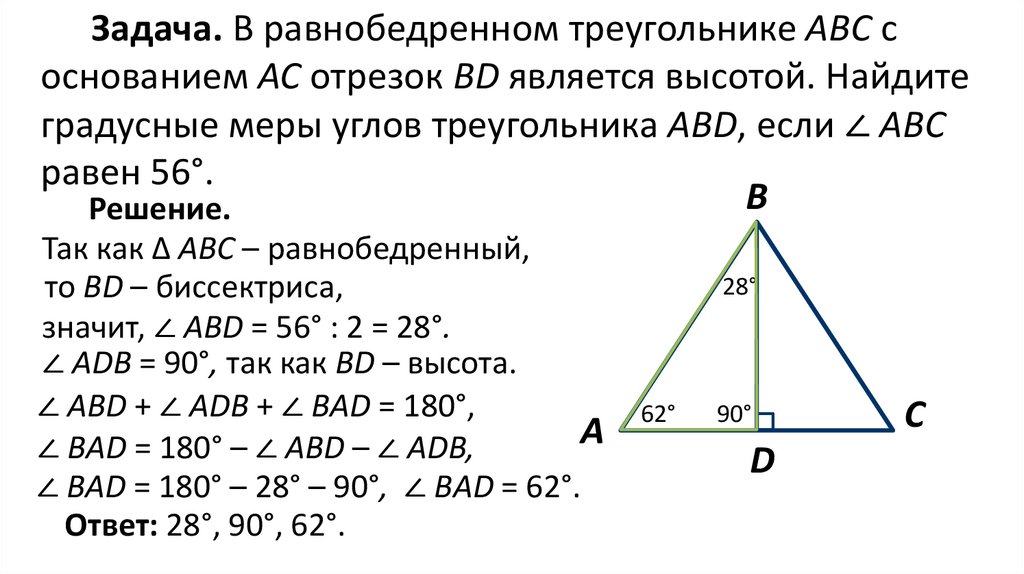
Задача. В равнобедренном треугольнике АВС с
основанием АС отрезок ВD является высотой. Найдите
градусные меры углов треугольника ABD, если ∠ АВС
равен 56°.
В
Решение.
Так как ∆ АВС – равнобедренный,
то ВD – биссектриса,
значит, ∠ АBD = 56° : 2 = 28°.
∠ АDВ = 90°, так как ВD – высота.
∠ АВD + ∠ АDB + ∠ ВAD = 180°,
А
∠ ВAD = 180° – ∠ АВD – ∠ АDB,
∠ ВAD = 180° – 28° – 90°, ∠ ВAD = 62°.
Ответ: 28°, 90°, 62°.
28°
62°
90°
D
С