Внутренний угол треугольника. Теорема о внешнем угле треугольника. Сумма углов треугольника

1.

Внутренний угол
треугольника.
Теорема о внешнем
угле треугольника.
Сумма углов
треугольника

2.

№1 Найти сумму
углов 1,2 и 3.
1
2 3
• 180◦
№2 Найти равные углы
3
1
1
2
4
3
4
2

3.

Найти градусную меру всех углов
в треугольнике, а так же сумму углов
в треугольнике.
70◦
1
30◦
80◦
2

4.

Попробуем геометрически
найти сумму углов в B
< 1 + < 2 + < 3 = 180о
треугольнике!
3
<А+<В+<С=?
< А + < В + < С = 180о
A
1
2
C
Случайно ли сумма углов в треугольнике АВС равна 180
градусов? Или этим свойством обладает любой
треугольник?

5.

Теорема.
Сумма углов треугольника равна 180о.
В
b
4 2 5
АВС
Доказать < А + < В + < С = 180о
1
3
1) Д.п.: b
AC; B b
А
Дано:
С
Доказательство.
2) < 1 и < 4 – накрест лежащие при АС
b и секущей АВ
<1=<4
3) < 3 и < 5 – накрест лежащие при АС
b и секущей BC
<3=<5
4)
< 4 + < 2 + < 5 = 180о ( развернутый угол)
< 1 + < 2 + < 3 = 180о
< А + < В + < С = 180о

6.

Чему равна градусная мера
неизвестного угла
треугольника
изображенного на
рисунке.
1.
х
Чему равна градусная мера
неизвестного угла
треугольника
изображенного на рисунке
1.
60°
х
80°
а)50º б)45º в)40º
2.
110°
40°
б) 40º в)30º
а) 35º
2.
х
х
40°
а) 90º б) 100º в)70º
35°
а)100º б)110º в)90º

7.

Пифагор
• Первое доказательство теоремы
о сумме углов треугольника было
сделано еще Пифагором (V в. до
н.э.). Великий ученый Пифагор
родился около 570 г. до н.э. на
острове Самосе. Отцом
Пифагора был Мнесарх, резчик
по драгоценным камням. Имя же
матери Пифагора неизвестно. По
многим античным
свидетельствам, родившийся
мальчик был сказочно красив, а
вскоре проявил и свои
незаурядные способности.

8.

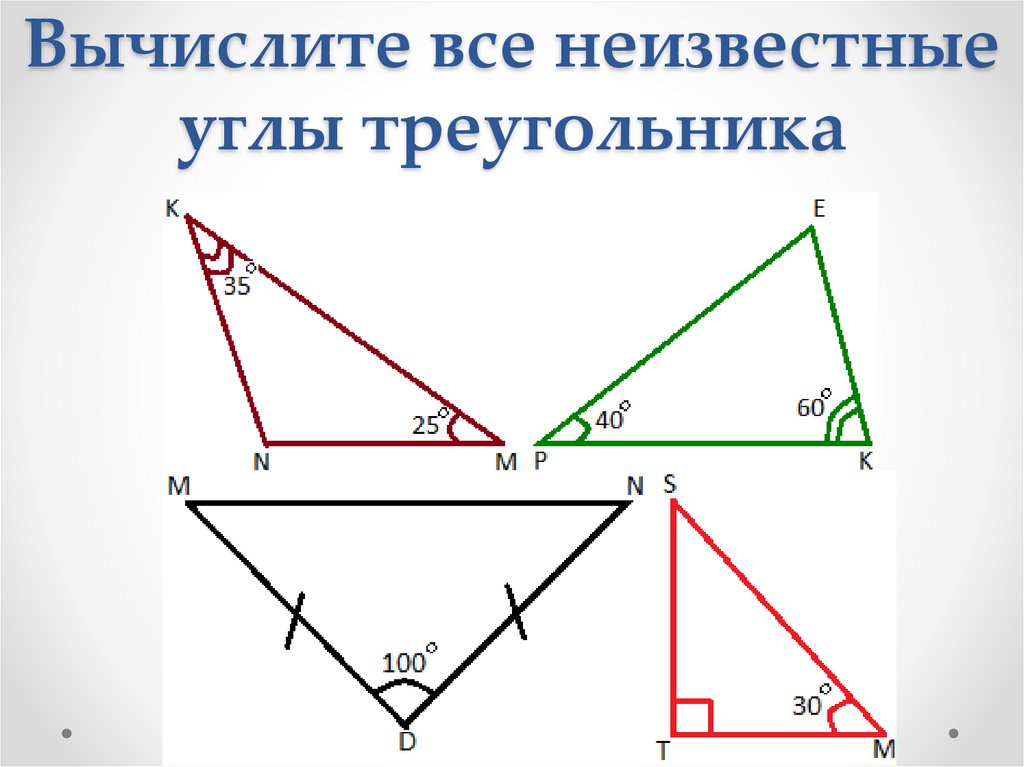
Вычислите все неизвестные
углы треугольника

9.

Вычислите все неизвестные
углы треугольника

10.

Виды углов
Острый
Прямой
Развернутый
Тупой

11.

Виды углов
Вертикальные углы. 1= 2, 3= 4
Смежные углы
1+ 2=180
Накрест лежащие углы. 1= 2
Односторонние углы. 2+ 3=180
Соответственные углы. 2= 4

12.

Определение внешнего
угла треугольника
• Внешним углом треугольника называется
угол смежный с каким-нибудь углом
треугольника.

13.

Теорема о внешнем
угле треугольника
• Внешний угол треугольника равен сумме
двух углов треугольника, не смежных с
ним.
Дано: ∆ABC, 4 – внешний.
Доказать: 4= 1+ 2.
Доказательство:
1. 4 – внешний угол,
смежный с 3
2. 4+ 3=180
3. ( 1+ 2)+ 3=180
4. 4= 1+ 2

14.

Назвать внешние углы в треугольнике
АВС.
В
6
7
2
4
1
А
9
3
5
8
С
Сколько можно построить внешних углов в
треугольнике?
Какую особенность в отношении внешних углов
вы заметили на чертеже?

15.

Повторение.
А
А
< 90о
Виды углов.
B
90о < B < 180о
Острый
угол
Тупой
угол
D
D = 180о
Развернутый угол
C
С = 90о
Прямой
угол
Теорема. Сумма углов треугольника равна 180о.
В
< А + < В + < С = 180о
А
С

16.

B
C
Треугольник, у которого все три угла острые.
называется остроугольным.
A
А
Треугольник, у которого один угол тупой,
называется тупоугольным.
B
C
А
Катет
Треугольник, у которого один угол прямой,
называется прямоугольным.
Гипотенуза лежит против прямого угла.
Катеты образуют прямой угол.
C
Катет
B

17.

По углам.
B
1. Остроугольный треугольник.
Все три угла острые.
C
A
A
2. Тупоугольный треугольник.
Один угол тупой, остальные - острые.
C
B
A
C
B
3. Прямоугольный треугольник.
а) Один угол прямой, остальные – острые.
б) Гипотенуза лежит против прямого угла.
в) Катеты образуют прямой угол.

18.

По сторонам.
1. Равнобедренный треугольник.
B
A
а) Треугольник, у которого 2 стороны
равны, называется равнобедренным.
б) Углы при основании равны.
в) Биссектриса, проведенная к основанию,
является медианой и высотой.
С
2.Равносторонний треугольник.
B
60o
A
60o
60o
C
B
A
а) Треугольник, у которого все стороны
равны, называется равносторонним.
б) Все углы по 60о.
в) Выполняется свойство биссектрисы
равнобедренного треугольника.
3. Разносторонний треугольник.
Все стороны разной длины.
C