Похожие презентации:
Интегральное исчисление
1.
Дисциплина: «Математика»Специальность: «Лечебное дело»
Курс: 1
2.
Функция F(x) называется первообразной дляфункции f(x), если выполняется равенство
F’(x)=f(x)
Нахождение первообразной для данной функции
называется интегрированием функции
Свойства первообразной
1. Если F(x) является первообразной для функции
f(x), то и функции F(x)+c тоже является
первообразной для f(x), где c–это константа.
2. Если F1 (x) и F2(x) первообразные функции f(x),
то они отличаются на константу, т. е. F1(x)-F2(x)
=c
3.
Совокупность всех первообразных называетсянеопределенным интегралом
f ( x)dx F ( x) c
Свойства неопределенного интеграла:
1.
сf
(
x
)
dx
с
f
(
x
)
dx
4.
2.( f ( x) g ( x))dx f ( x)dx g ( x)dx
3.
4.
F
'
(
x
)
dx
F
(
x
)
c
d ( f ( x)dx) f ( x)dx
5.
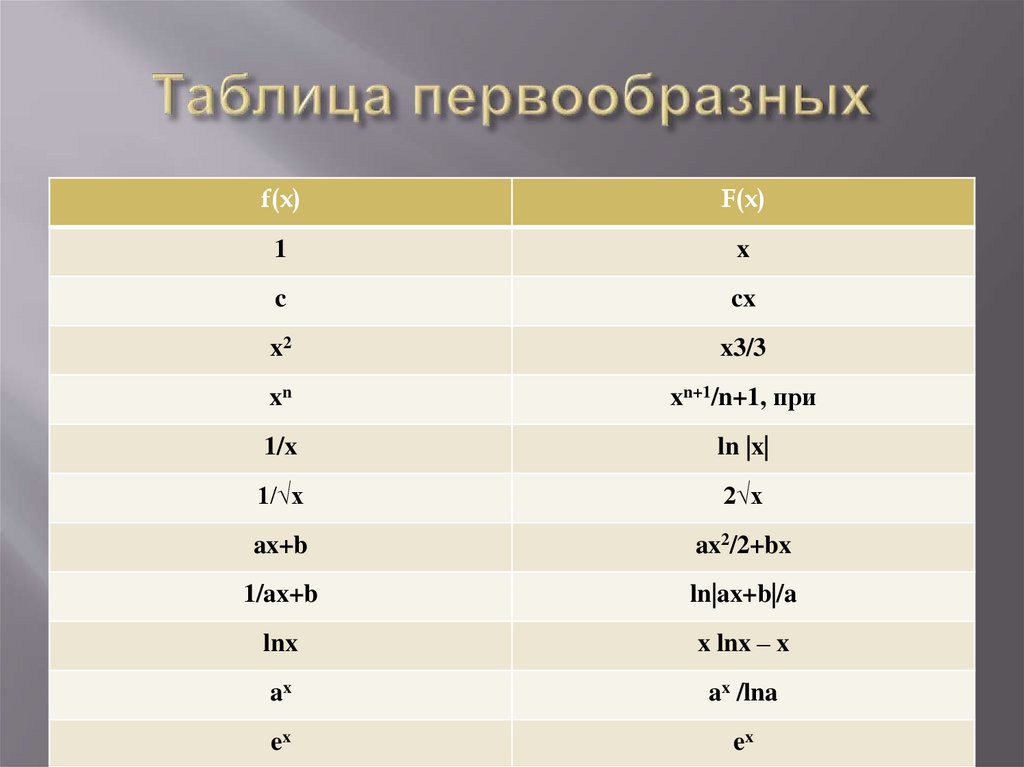
f(x)F(x)
1
x
c
cx
x2
x3/3
xn
xn+1/n+1, при
1/x
ln |x|
1/√x
2√x
ax+b
ax2/2+bx
1/ax+b
ln|ax+b|/a
lnx
x lnx – x
ax
ax /lna
ex
ex
6.
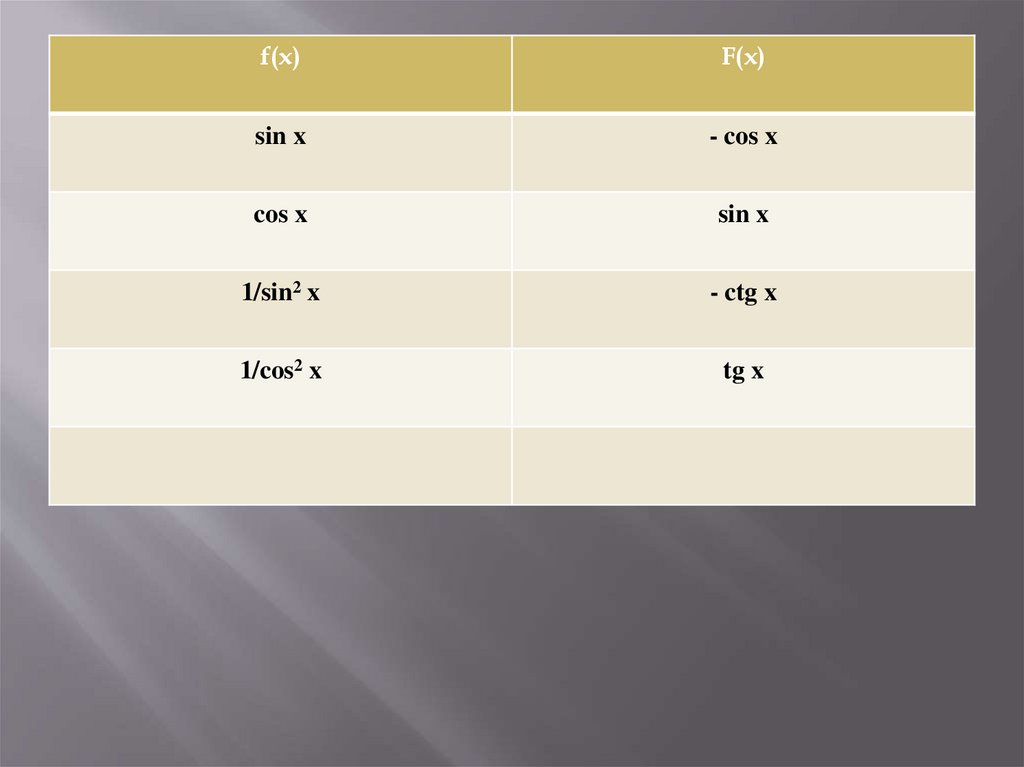
f(x)F(x)
sin x
- cos x
cos x
sin x
1/sin2 x
- ctg x
1/cos2 x
tg x
7.
Непосредственное интегрированиеИнтегралы вычисляются с помощью свойств и
табличных формул
Пример:
1.
(
3
sin
x
5
x
e
)
dx
9
x
8.
2. Замена переменнойДля вычисления интегралов вводится новая
переменная t, через которую выражается исходная
функция f(x) и исходный дифференциал dx.
Вычисляется интеграл относительно новой
переменной t, получается первообразная F(t) и
делается обратная замена – выражаем t через
выражение содержащее x
Пример:
(
5
x
8
)
dx
7
9.
3. Интегрирование по частямДля вычисления интегралов используется формула:
udv
uv
vdu
где u и dv части исходного интеграла. Чтобы
применить формулу необходимо найти v и du,
применяя формулы для нахождения дифференциала
и интеграла
Пусть u = f(x), тогда du = f’(x)dx;
dv = g(x)dx, следовательно v = ∫g(x)dx
10.
Пример:e
sin
xdx
x
u = sin x | du = (sin x)’dx = cos x dx
dv = exdx | v = ∫exdx = ex
11.
Интеграл взятый на определенном отрезкеназывается определенным интегралом
b
f ( x) dx
a
a и b – пределы интегрирования, a – нижний
предел, b – верхний предел (a < b)
Для решения определенного интеграла применяется
формула Ньютона-Лейбница:
b
a
f ( x)dx F ( x)
b
a
F (b) F (a)
12.
1.2.
3.
b
b
a
a
c f ( x)dx c f ( x)dx
b
b
b
a
a
a
( f ( x) g ( x))dx f ( x)dx g ( x)dx
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx
4. Если f(x) ≤ g(x) на интервале [a; b], то
b
a
b
f ( x)
g ( x)
a
13.
1.Нахождение площади фигуры, ограниченной
функцией (функциями):
b
S
f ( x) dx
a
b
S
a
b
f ( x)dx g ( x)dx
a
где f(x) ограничивает фигуру сверху, g(x)
ограничивает фигуру снизу
14.
2. Нахождение объёма тела вращения,ограниченного функцией:
b
V f ( x)dx
2
a
3. Нахождение длины дуги кривой:
b
L ( f ' ( x)) 1
2
a
15.
Уравнения содержащие аргумент, функцию и еёпроизводные называются дифференциальными
уравнениями
Решением дифференциального уравнения является
функция y = φ (x; c), где c – константа.
При решении дифференциального уравнения
производная заменяется на отношение
дифференциалов:
dy
y'
dx
16.
Чтобы выразить функцию через аргументнеобходимо избавиться от дифференциалов. Для
этого необходимо проинтегрировать выражение.
Результатом будет функция y = φ (x; c), которая
называется общим решением дифференциального
уравнения (т.к. вместо с можно подставить любое
число). Если константа принимает конкретное
числовое значение, то из общего решения
выделяется частное решение дифференциального
уравнения. Для этого необходимо знать начальные
условия: y = y0 при x = x0 или y0 = f (x0)



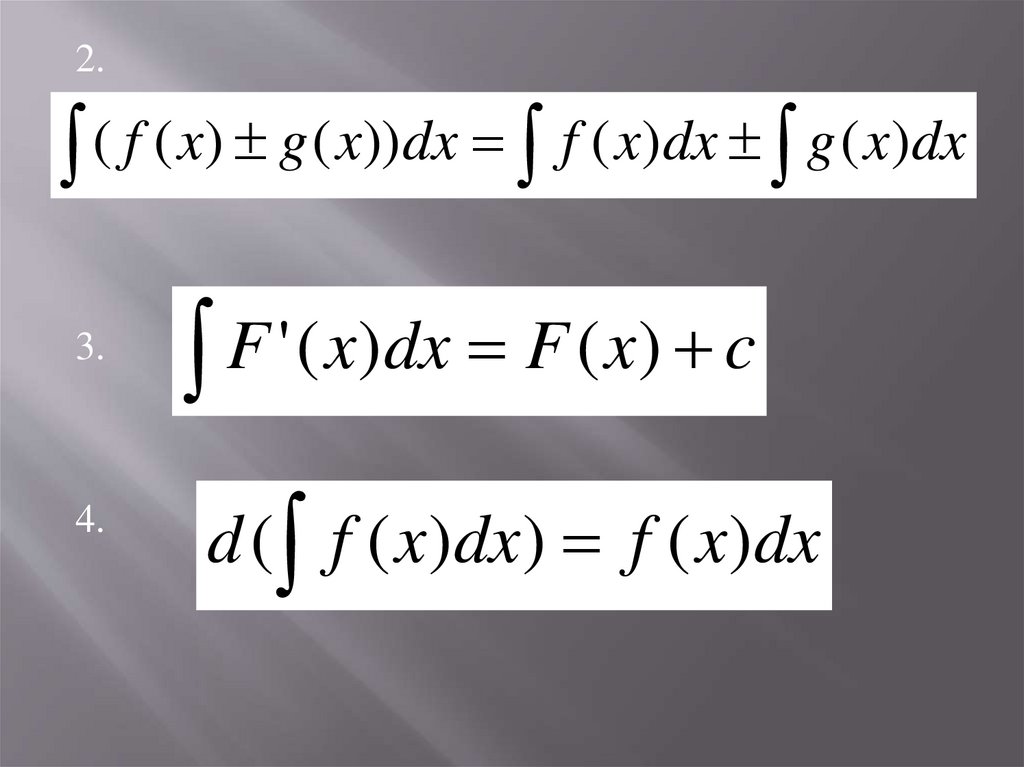










 Математика
Математика








