Магнитное поле. Тема 7

1.

Тема 7
Магнитное поле
1

2.

ПЛАН ЛЕКЦИИ
1.Магнитное поле. Вектор магнитной индукции.
Поток вектора магнитной индукции.
2. Закон Ампера. Контур с током в магнитном
поле.
3. Напряженность магнитного поля. Закон Био—
Савара— Лапласа.
4. Применение закона Био—Савара— Лапласа к
расчету магнитного поля.
5. Закон полного тока.
6. Действие магнитного поля на движущийся
заряд. Сила Лоренца.
7. Эффект Холла.
2

3.

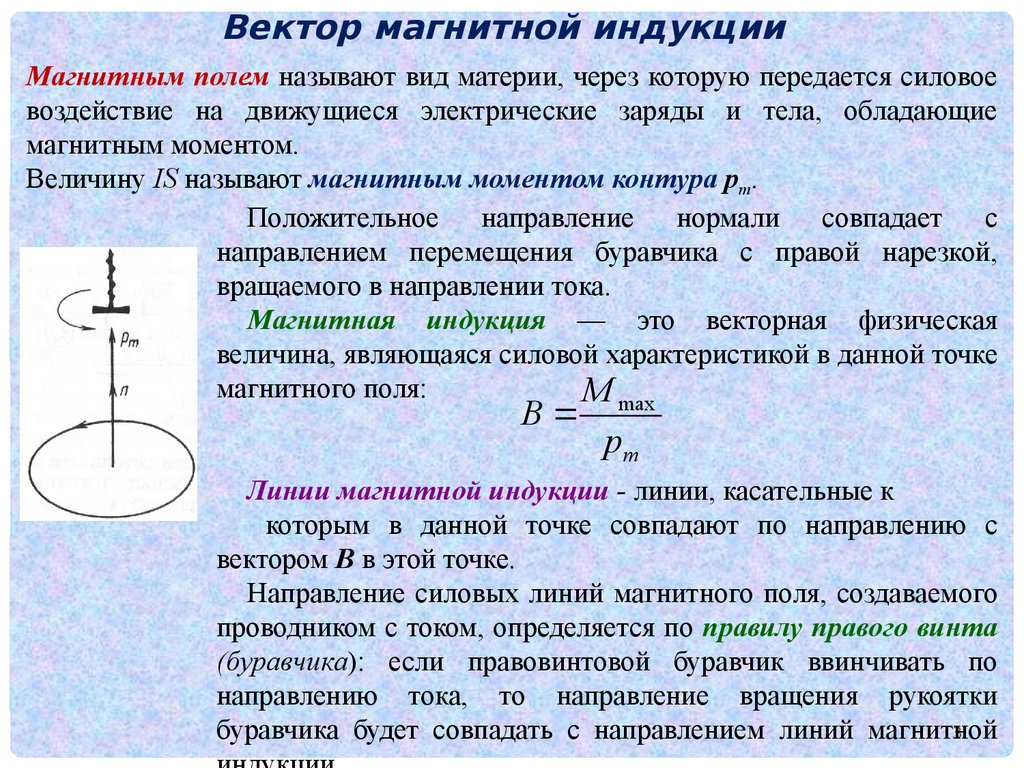
Вектор магнитной индукции
Магнитным полем называют вид материи, через которую передается силовое
воздействие на движущиеся электрические заряды и тела, обладающие
магнитным моментом.
Величину IS называют магнитным моментом контура pm.
Положительное направление нормали совпадает с
направлением перемещения буравчика с правой нарезкой,
вращаемого в направлении тока.
Магнитная индукция — это векторная физическая
величина, являющаяся силовой характеристикой в данной точке
магнитного поля:
M max
B
pm
Линии магнитной индукции - линии, касательные к
которым в данной точке совпадают по направлению с
вектором В в этой точке.
Направление силовых линий магнитного поля, создаваемого
проводником с током, определяется по правилу правого винта
(буравчика): если правовинтовой буравчик ввинчивать по
направлению тока, то направление вращения рукоятки
буравчика будет совпадать с направлением линий магнитной
3

4.

Линии магнитной индукции прямого проводника с током представляют
концентрические окружности, лежащие в плоскости, перпендикулярной току.
Центр этих окружностей находится на оси проводника.
Линии магнитной индукции всегда замкнуты и охватывают проводники с
токами. Это отличает их от линий напряженности электрического поля.
Замкнутость линий магнитной индукции говорит о том, что в природе не
существует магнитных зарядов, на которых бы они начинались или кончались.
Такие поля называют соленоидальными или вихревыми.
Циркуляция вектора магнитной индукции по любому замкнутому контуру
не равна нулю:
(2)
⃗
∮ В d r⃗ ≠ 0
В отличие от потенциального, каким является электростатическое поле
∮ E r dr =0
Магнитное поле называют однородным, если векторы магнитной индукции во
всех его точках одинаковы:
В=const.
(3)
Примером однородного магнитного поля может служить поле внутри
соленоида, т.е. катушки, длина которой много больше ее диаметра. Линии
магнитной индукции однородного поля параллельны, и их густота везде
одинакова.

5.

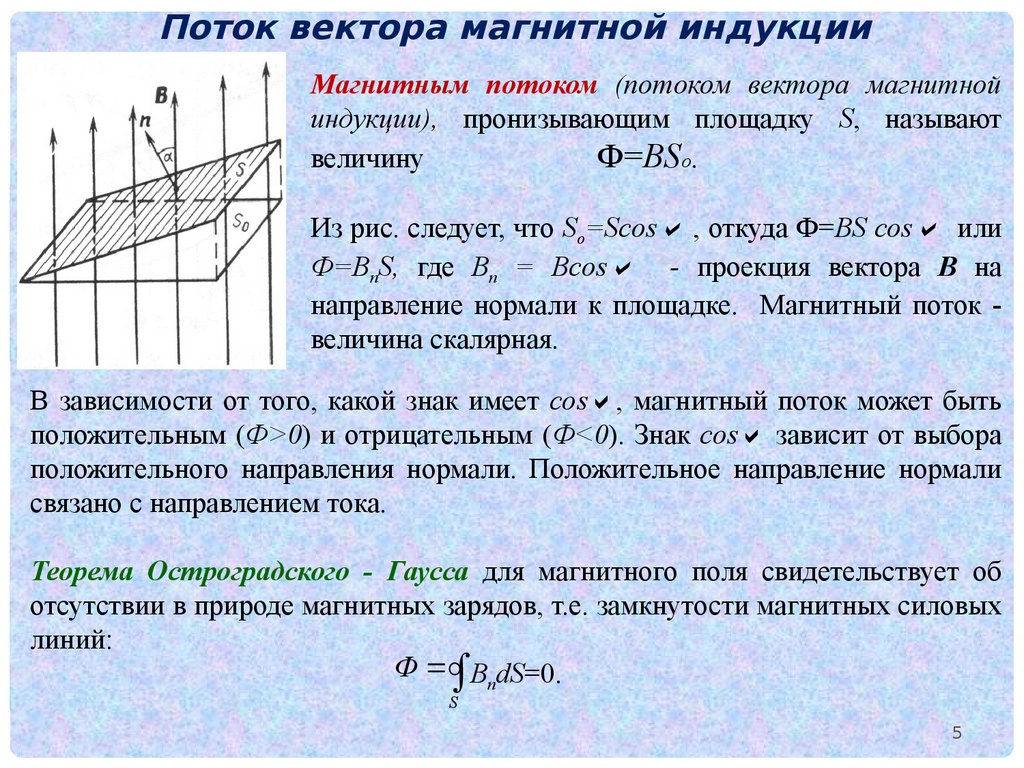
Поток вектора магнитной индукции
Магнитным потоком (потоком вектора магнитной
индукции), пронизывающим площадку S, называют
величину
Ф=BSо.
Из рис. следует, что Sо=Scos , откуда Ф=BS cos или
Ф=ВnS, где Bn = Bcos - проекция вектора В на
направление нормали к площадке. Магнитный поток величина скалярная.
В зависимости от того, какой знак имеет cos , магнитный поток может быть
положительным (Ф>0) и отрицательным (Ф<0). Знак cos зависит от выбора
положительного направления нормали. Положительное направление нормали
связано с направлением тока.
Теорема Остроградского - Гаусса для магнитного поля свидетельствует об
отсутствии в природе магнитных зарядов, т.е. замкнутости магнитных силовых
линий:
Ф ВndS=0.
S
5

6.

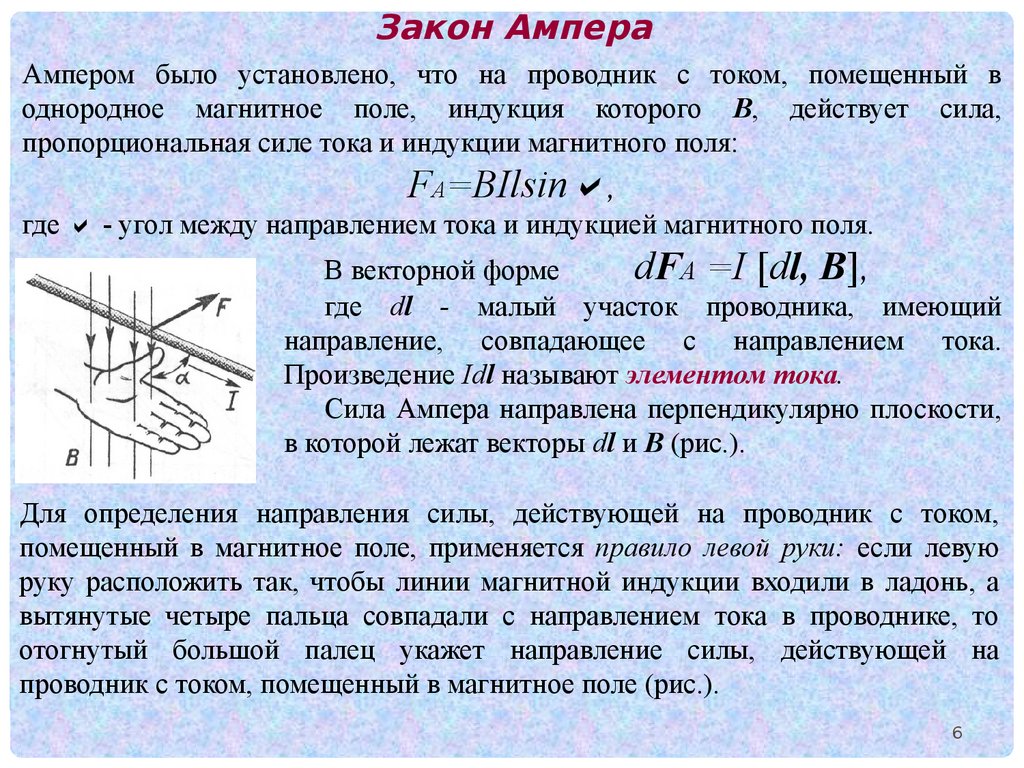
Закон Ампера
Ампером было установлено, что на проводник с током, помещенный в
однородное магнитное поле, индукция которого В, действует сила,
пропорциональная силе тока и индукции магнитного поля:
FА=BIlsin ,
где - угол между направлением тока и индукцией магнитного поля.
В векторной форме
dFА =I [dl, B],
где dl - малый участок проводника, имеющий
направление, совпадающее с направлением тока.
Произведение Idl называют элементом тока.
Сила Ампера направлена перпендикулярно плоскости,
в которой лежат векторы dl и В (рис.).
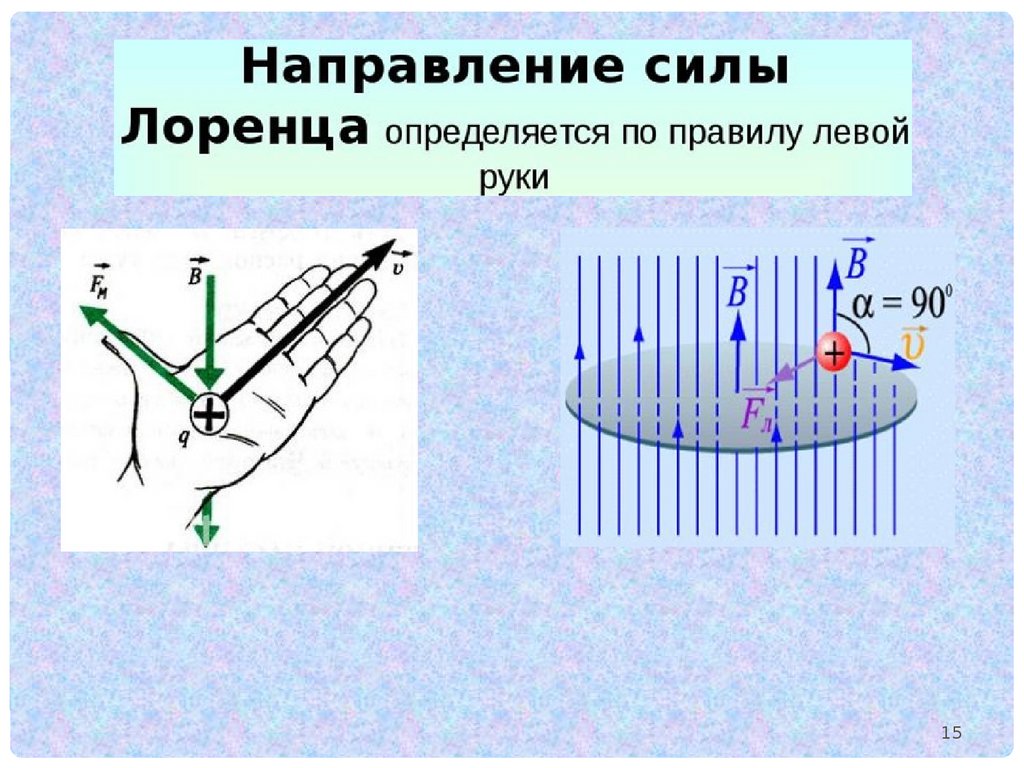
Для определения направления силы, действующей на проводник с током,
помещенный в магнитное поле, применяется правило левой руки: если левую
руку расположить так, чтобы линии магнитной индукции входили в ладонь, а
вытянутые четыре пальца совпадали с направлением тока в проводнике, то
отогнутый большой палец укажет направление силы, действующей на
проводник с током, помещенный в магнитное поле (рис.).
6

7.

Контур с током в магнитном поле
Контур с током, имеющий стороны а и l, помещен
в магнитное поле (рис.). На каждую сторону
контура
действует
сила
Ампера.
На
горизонтальные стороны l контура действуют
силы, которые растягивают или сжимают контур,
не поворачивая его. На каждую из вертикальных
сторон а действует сила F=IBa.
Эти силы создают пару сил, момент которой
M = Fl cos ,
где — угол между вектором В и стороной контура l.
Момент сил стремится повернуть контур так, чтобы поток Ф, пронизывающий
контур, был максимальным.
Подставляя выражение для силы в формулу для момента силы:
М = IBal cos ,
где al=S, IS=pm, cos =cos( 2 ) sin , тогда M = Bpm sin .
Механический момент М, действующий на контур с током в однородном
магнитном поле, пропорционален магнитному моменту pm, контура, индукции
В магнитного поля и синусу угла между направлением векторов pm и В.
В векторной форме соотношение имеет вид: М=[pm, В].
7

8.

Напряженность магнитного поля.
Закон Био – Савара - Лапласа
Величина, показывающая, во сколько раз магнитная индукция в данной
однородной изотропной среде больше или меньше, чем в вакууме, называется
относительной магнитной проницаемостью среды: В
Во
Магнитное поле в вакууме принято характеризовать не индукцией Во, а
напряженностью Н магнитного
поля. Эти две физические величины связаны
Bo или
между собой:
H
Bo o H , где o=4 10-7 Гн/м - магнитная
o
постоянная.
Обобщая экспериментальные данные французских физиков
Био и Савара, Лаплас (французский математик) предложил
формулу, по которой можно вычислять напряженность поля,
создаваемого элементом тока в точке М, расположенной от
этого элемента на расстоянии r :
Idl sin
dH
4 r
2
.
Напряженность Н в любой точке магнитного поля проводника с
током I равна векторной сумме напряженностей dH,
элементарных полей, создаваемых всеми участками проводника
(принцип суперпозиции полей): n
H H i
i 1
8

9.

Применение закона Био – Савара - Лапласа
к расчету магнитного поля
1. Магнитное поле прямолинейного бесконечно длинного
проводника с током
Из рис. видно, что
dl sin dl cos dS
d ,
r
r
r
r
ro
cos
Подставляя эти выражения в формулу Био – Савара Лапласа,
находим,
напряженность,
создаваемая
элементом тока Idl:
dH
Idl sin
I
cos d
2
4 r
4 ro
Чтобы определить напряженность магнитного поля, создаваемого бесконечно
длинным прямолинейным проводником с током, нужно проинтегрировать
последнее выражение в пределах от - /2 до + /2:
I
H
4 ro
/2
cos d
/2
I
4 ro
9

10.

Применение закона Био – Савара - Лапласа
к расчету магнитного поля
2. Магнитное поле в центре кругового тока
Пусть ток протекает по окружности. В этом случае все
элементы проводника перпендикулярны радиусу - вектору
r и sin =l. Расстояние всех элементов проводника до
центра одинаково и равно r. Поэтому напряженность поля
в центре кругового проводника: dH Idl
4 r 2
Так как все элементы тока создают поле, напряженность которого одинаково
направлена, то напряженность поля в центре кругового проводника:
I
H
4 r 2
2 r
dl
0
I
I
2
r
2r
4 r 2 o
3. Магнитное поле движущегося заряда
Рассмотрим отрезок проводника длиной dl с током I. Он создает в некоторой
точке, удаленной на расстояние r, поле напряженностью
Idl sin
dH
Напряженность поля, создаваемого одной заряженной
4 r 2
частицей:
e [⃗υ r⃗ ]
e sin
⃗
H=
H
3
2
4
πr
10
4 r

11.

Закон полного тока
Циркуляцией вектора Н по замкнутому контуру называется интеграл
Hdl H e dl ,
L
L
где dl - вектор элементарной длины контура, направленной вдоль обхода контура,
Не=Нcos - составляющая вектора Н в направлении касательной к контуру, угол между векторами В и dl.
Выберем в магнитном поле бесконечно прямолинейного проводника с током I
произвольный контур, совпадающий с одной из силовых линий, охватывающих
ток. Силовые линии бесконечно длинного прямолинейного проводника
представляют собой концентрические окружности.
В каждой точке этого контура вектор Н одинаков по модулю, следовательно,
2 ro
циркуляция вектора Н:
I
I
Hdl 2 r
L
L
o
dl
2 ro
dl I ,
0
I
где ro — радиус выбранной силовой линии, т.е. окружности:
2 ro
Соотношение связывает циркуляцию вектора напряженности магнитного поля и
ток и называется законом полного тока.
n
Циркуляция вектора напряженности магнитного
Hdl I i
поля по контуру равна алгебраической сумме токов,
11
i 1
L
охватываемых этим контуром:
H

12.

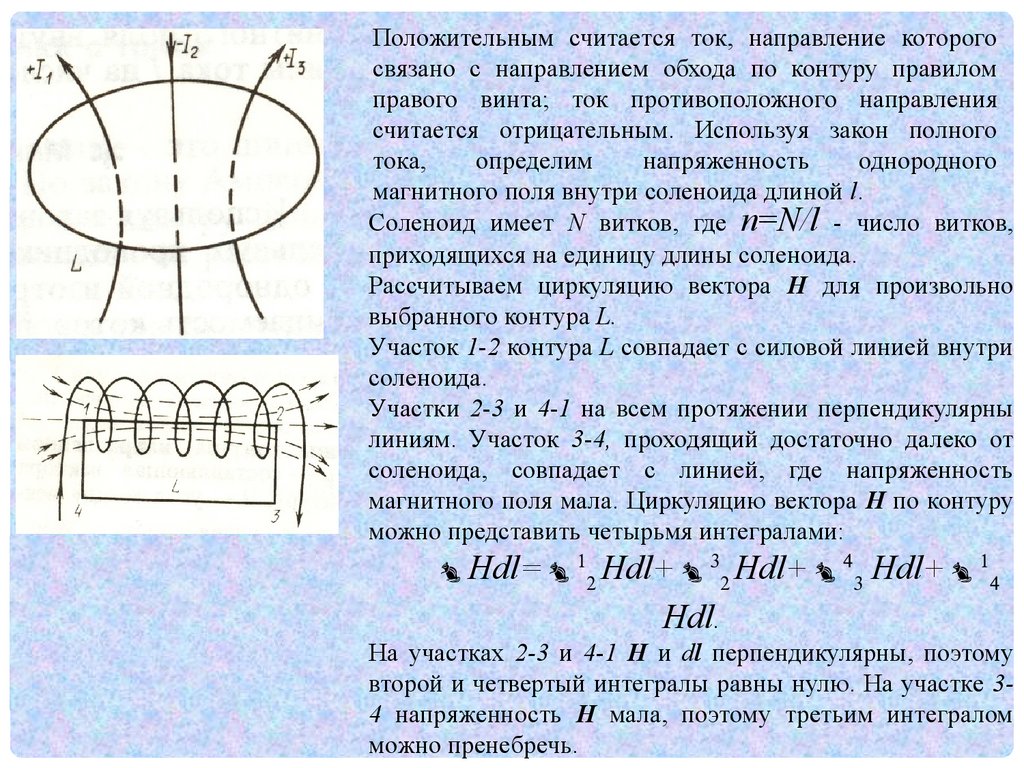
Положительным считается ток, направление которого
связано с направлением обхода по контуру правилом
правого винта; ток противоположного направления
считается отрицательным. Используя закон полного
тока,
определим
напряженность
однородного
магнитного поля внутри соленоида длиной l.
Соленоид имеет N витков, где п=N/l - число витков,
приходящихся на единицу длины соленоида.
Рассчитываем циркуляцию вектора Н для произвольно
выбранного контура L.
Участок 1-2 контура L совпадает с силовой линией внутри
соленоида.
Участки 2-3 и 4-1 на всем протяжении перпендикулярны
линиям. Участок 3-4, проходящий достаточно далеко от
соленоида, совпадает с линией, где напряженность
магнитного поля мала. Циркуляцию вектора Н по контуру
можно представить четырьмя интегралами:
Hdl= 12 Hdl+ 32 Hdl+ 43 Hdl+ 14
Hdl.
На участках 2-3 и 4-1 H и dl перпендикулярны, поэтому
второй и четвертый интегралы равны нулю. На участке 34 напряженность Н мала, поэтому третьим интегралом
можно пренебречь.

13.

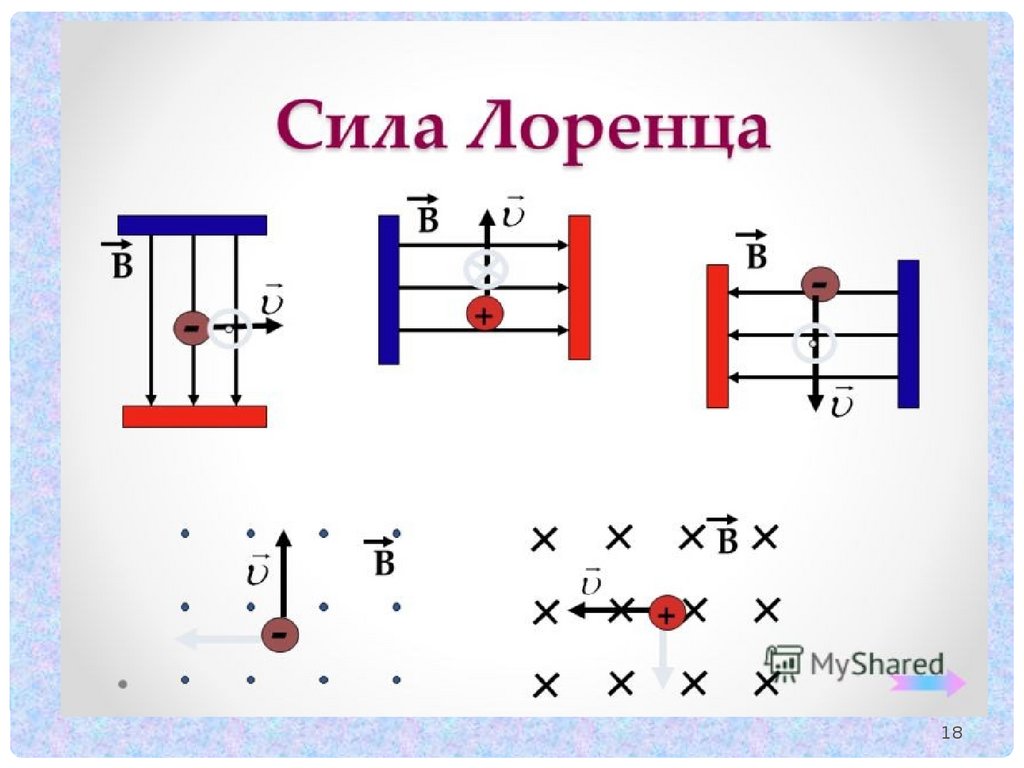
Действие магнитного поля на движущийся заряд.
Сила Лоренца
13

14.

Действие магнитного поля на движущийся заряд.
Сила Лоренца
14

15.

15

16.

Действие магнитного поля на движущийся заряд.
Сила Лоренца
16

17.

Действие магнитного поля на движущийся заряд.
Сила Лоренца
17

18.

18

19.

19

20.

Эффект Холла
Американский
ученый
Э.
Холл
обнаружил,
что
в
проводнике,
помещенном
в
магнитное
поле,
возникает
разность
потенциалов
(поперечная)
в
направлении,
перпендикулярном вектору магнитной
индукции В и току I, вследствие
действия силы Лоренца на заряды,
движущиеся в этом проводнике.
Опыт показывает, что поперечная разность потенциалов пропорциональна
плотности тока j, магнитной индукции и расстоянию а между электродами:
U=RаjB,
где R — постоянная Холла, зависящая от рода вещества,
R=1/пе.
Постоянная Холла зависит от концентрации
электронов. Поэтому, измеряя постоянную R,
можно определить концентрацию электронов
внутри проводника.
20