C38. Задача с прямоугольным параллелепипедом

1.

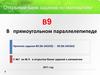
Дан прямоугольный параллелепипед ABCDA1B1C1D1, длины ребер
которого АВ = 2, AD = AA1 = 1. Найдите угол между плоскостями
CD1B1 и CDA1.
Построим сечения параллелепипеда заданными плоскостями.
B1C1D1 = CDD1, по катетам. Сечение CD1B1 – это равнобедренный
треугольник, СD1 = D1B1.
C1
D1 CDA1 – диагональное сечение,
прямоугольник CDA1B1.
Построим линейный угол двугранного
B1
A1
угла D1BCD (ВС – ребро).
Медиана D1F равнобедренного
1 треугольника является и высотой.
a
N
F
C
D
1
B
2
A
Из точки F в прямоугольнике проведем
линию параллельно стороне
прямоугольника СD. Она будет
перпендикулярна сторонам В1С и А1D.
Точки F и N – это точки пересечения
диагоналей граней ВСС1В1 и ADD1A1.
FN ADD1 FN ND1

2.

Дан прямоугольный параллелепипед ABCDA1B1C1D1, длины ребер
которого АВ = 2, AD = AA1 = 1. Найдите угол между плоскостями
CD1B1 и CDA1.
Из
В
FD
Из FND
Из
C ВD
Из BCВ11
2
2 2
2
2
FN2 BВ 2 ;
D11D
В11
В
FD
В
C FВ
C1 D
1 1; ; cos
CВ1a BC
;
1
2
FD
2
2
2
2
В1 D12 1 22 ; 2 CВ1 12 112 ;
;
2
D1 5 2 FD1
2
В1 D1 5;
CВ1a 2;3 ;
2 cos
2 51;
В
D
CВ1 22;
1
1
FD
;
A1
1 5
2
В1 D1 5.
CВ1 2 . 2
cos a 2
;
1
1
3 2 .
FD1 4 ;
Тогда
FВ
1
2
N
2 2 2
cos a
.
9
3
FD1 ;
2
2 2
a
arccos
.
D
3
3
FD1
1
2
1 11 11
22
1 11
C1
2
1
5
B1
3
2
2
2
a
F
C
B
2
2
A