Похожие презентации:
Прямоугольный параллелепипед. Задача
1.
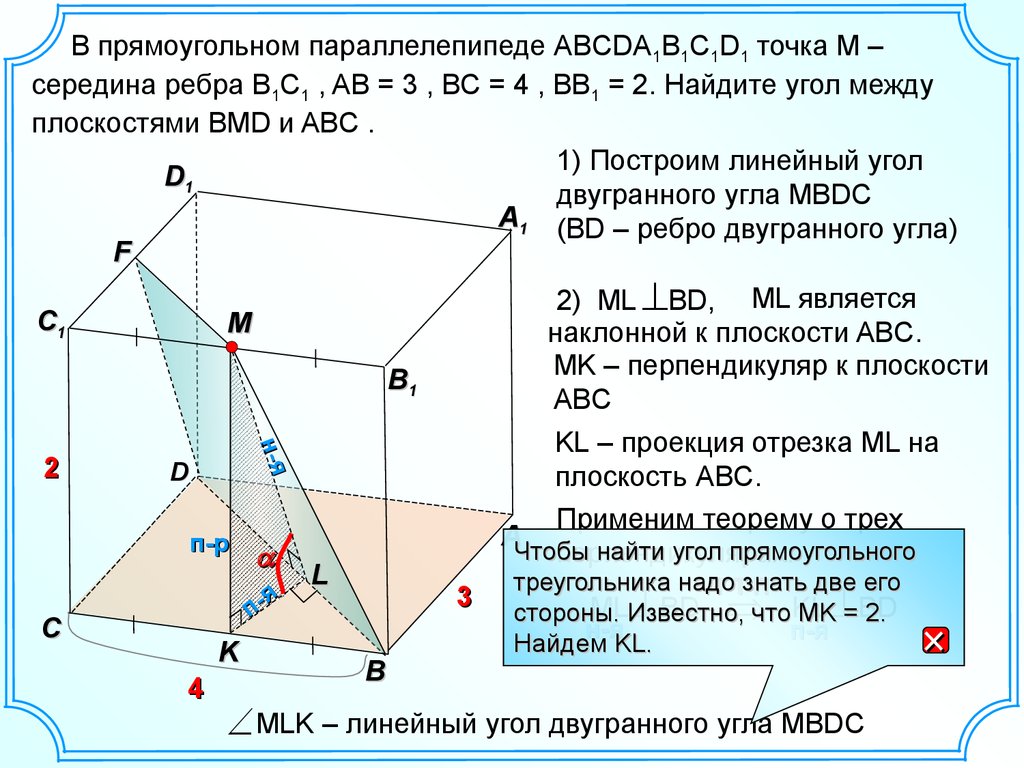
В прямоугольном параллелепипеде ABCDA1B1C1D1 точка M –середина ребра B1C1 , AB = 3 , BC = 4 , BB1 = 2. Найдите угол между
плоскостями BMD и ABC .
1) Построим линейный угол
D1
двугранного угла MBDC
A1 (BD – ребро двугранного угла)
F
C1
2) ML BD, ML является
наклонной к плоскости ABC.
MK – перпендикуляр к плоскости
ABC
KL – проекция отрезка ML на
плоскость ABC.
Применим теорему о трех
AЧтобы найти угол прямоугольного
перпендикулярах.
M
B1
н-я
2
D
п-р
я
п-
C
K
4
L
3
B
треугольника надо
две его
Т Тзнать
П
MLИзвестно,
BD чтоKL
стороны.
MK
=BD
2.
н-я
п-я
Найдем KL.
MLK – линейный угол двугранного угла MBDC
2.
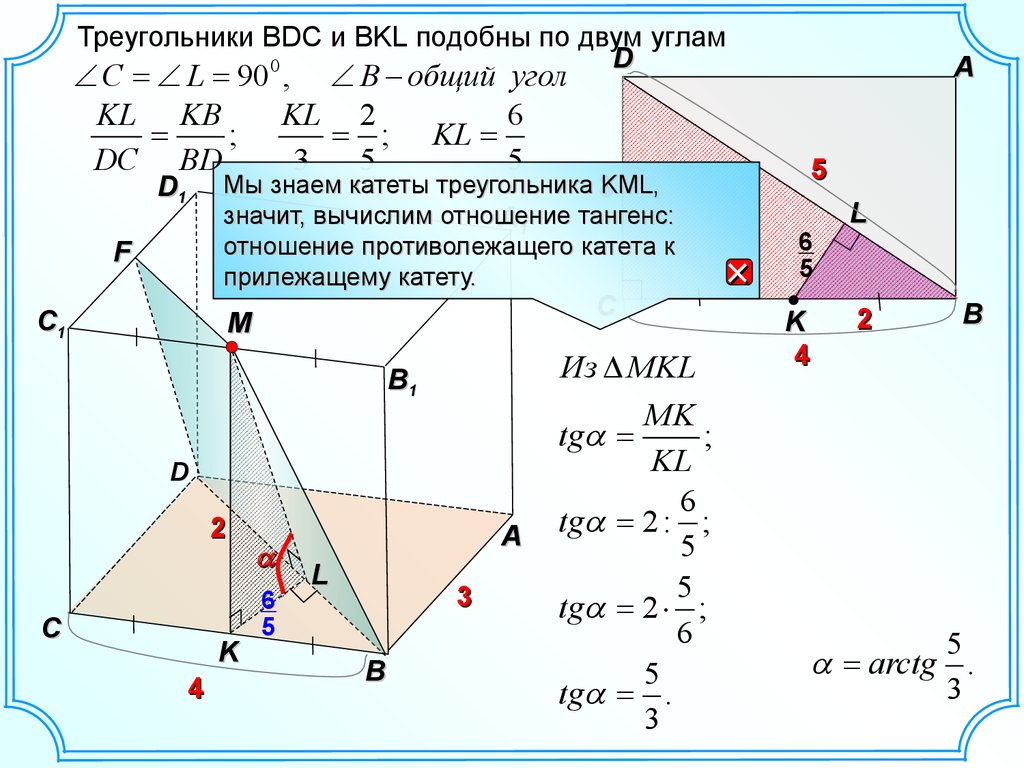
Треугольники BDC и BKL подобны по двум угламD
0
A
С L 90 , B общий угол
KL KB
KL 2
6
;
; KL
DC BD
3
5
5
Мы знаем катеты треугольника 3KML,
значит, вычислим отношение
тангенс:
A1
отношение противолежащего катета к
прилежащему катету.
D1
F
C1
C
M
Из MKL
B1
tg
D
2
C
K
4
6
5
A
L
3
B
tg
tg
tg
MK
;
KL
6
2: ;
5
5
2 ;
6
5
.
3
5
6
5
K
4
L
2
B
5
arctg .
3
 Математика
Математика








