В мире рациональных уравнений

1.

2.

Актуальность исследования
Приобретенные при изучении дополнительной научной
литературы навыки в дальнейшем позволят решать достаточно
широкий круг текстовых задач, что является актуальным при
изучении математики и смежных дисциплин.
Цель исследования:
систематизировать методы решения рациональных
уравнений и показать их применение при решении
нестандартных уравнений.

3.

Задачи:
отобрать научную литературу по данной теме;
научиться решать квадратные уравнения различными
методами;
познакомиться с понятием симметрических, возвратных и
однородных уравнений;
изучить методы решения рациональных уравнений;
научиться выбирать оптимальные способы решения
рациональных уравнений при решении нестандартных задач
по математике.
Объект исследования:
Предмет исследования:
рациональные уравнения
изучение приёмов решения нестандартных
задач, основанных на использовании
основных методов решения рациональных
уравнений

4.

Необходимость решать уравнения в
древности
была
вызвана потребностью в
Известный
арабский
математик
умении
делить
доходы и имущество,
Ал-Хорезми
в своей
книге
вычислять
площади
земельных участков
«Ал-джабар»
описал
способы
и стоимость
товара, находить объёмы
решения различных
уравнений,
фигур,
и определялась развитием
в том числе
и уравнений
астрономии
высших
степеней.и самой математики.
Их особенность была в том, что
Ал-Хорезми применял сложные
радикалы для нахождения
корней уравнений.
Ал-Хорезми

5.

Рациональное выражение с одной переменной – это
алгебраическое выражение, составленное из чисел и
переменной x с помощью операций сложения, вычитания,
умножения, деления и возведения в целую степень.
Уравнение f(x) = g(x) называется рациональным, если
f(x) и g(x) – рациональные выражения.
Если f(x) и g(x) – целые выражения, то уравнение
называют целым.
Рациональное уравнение f(x) = g(x) называется
дробным, если хотя бы одно из выражений f(x) или g(x)
является дробным.

6.

1. Простейшие преобразования. Достаточно выполнить обычные
упрощения: приведение к общему знаменателю, приведение
подобных членов и т.д.
2. Подстановка. Иногда при решении рациональных уравнений
имеет смысл ввести новую переменную, заменив ею некое
повторяющееся рациональное выражение.
3. Распадающееся уравнение. Рациональное уравнение называется
распадающимся, если его можно представить в виде P(x)Q(x) = 0, где
P(x) и Q(x) – целые рациональные функции.

7.

Биквадратное уравнение: ax 4 bx 2 с 0
Замена:
x2 = t,
t>0
2
2
аP
(
x
)
bP
(
x
)
Q
(
x
)
cQ
( x) 0
Однородное уравнение 2-ого порядка:
Замена:
Р( x)
t
Q( x)
Симметрическое уравнение 4-ого порядка: ax 4 bx 3 cx 2 bx a 0
Замена:
x
1
t
x
Возвратное уравнение 4-ого порядка: ax 4 bx 3 cx 2 kbx k 2 a 0
Замена:
x
Уравнение вида: ( ax 2 b1 x c )(аx 2 b2 x с ) kx 2
Замена:
k
t
x
ax
с
t
х

8.

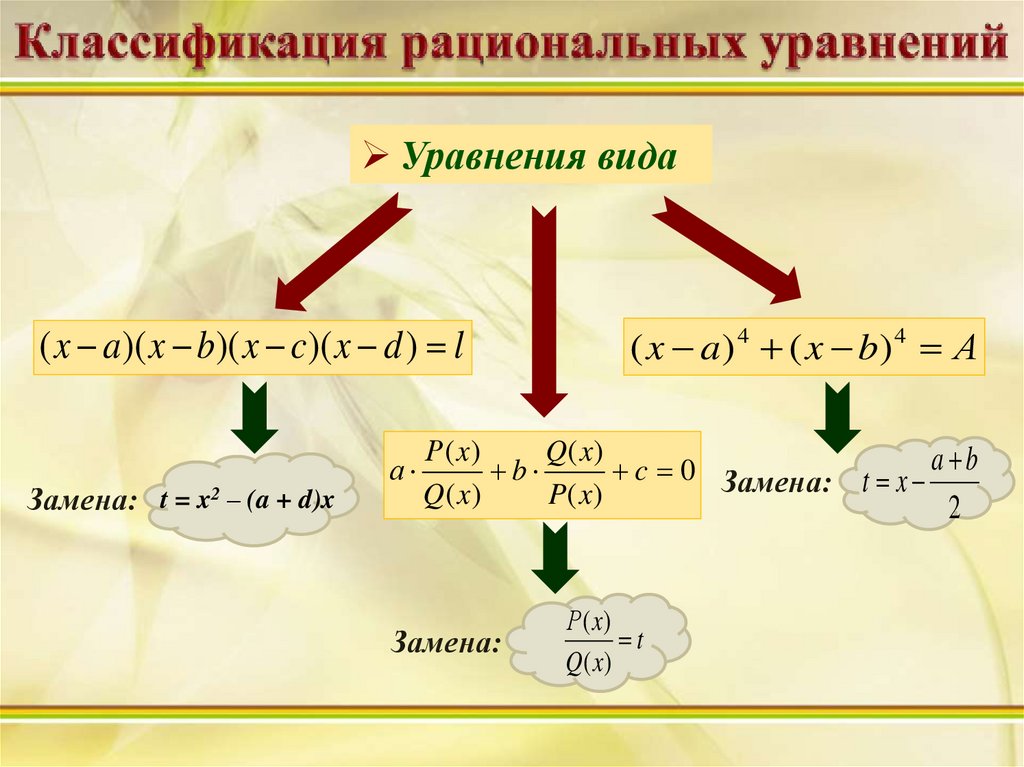
Уравнения вида
( x a)( x b)( x c)( x d ) l
Замена: t = x2 – (a + d)x
а
( x a ) 4 ( x b) 4 А
Р( x)
Q( x)
b
c 0 Замена:
Q( x)
P( x)
Замена:
Р( x)
t
Q( x)
a b
t x
2

9.

Приём почленного деления
( х 2 х 1) 2
9
Решите уравнение:
.
2
2
( х 1) ( х 1) 5
Решение.
5( x 2 x 1) 2 9( x 1) 2 ( x 2 1)
5( x 2 x 1) 2 9( x 2 2 x 1)( x 2 1)
2
х х 1
х 2 2х 1 х 2 1
9
5
,
х
х
х
1
1
1
5( x 1 ) 2 9( x 2 )( x )
x
x
x
2
1
x
Пусть x t , тогда 5(t 1) 2 9t (t 2)
5t 2 10t 5 9t 2 18t
4t 2 8t 5 0
D1 16 4 5 36
4 6
1
t1 , t 2 5
4
2
2
Вернёмся к замене:
1) x 1 1 2 x 2 x 2 0
x
2
t
D 0. Действительных корней нет.
2) x 1 5 2 x 2 5 x 2 0
x 2
1
1
Ответ: ; 2
x1 , x2 2.
2
2

10.

Приём выделения квадрата двучлена
81х 2
40.
Решите уравнение: х
2
(9 х)
2
Решение.
2
9х
9x
x
2
x
40,
9 х
9 x
2
x
1)
2,
9 x
2
x
2)
20,
9 x
x 2 2 x 18 0, x 2 20 x 180 0,
2
9 x x 9 х 18 x 2
40,
9 х
9 x
2
2
x
x2
18
40,
9 x
9 х
2
t1 2, t 2 20.
x2
2
Пусть
t , тогда t 18t 40 0,
9 x
D1 ( 1) 2 18 19,
x 1 19;
D1 0
Корней нет.
Ответ : 1 19 .

11.

В ходе исследования обобщены научные сведения по теме
«Рациональные уравнения»:
приведена классификация рациональных уравнений;
сформулированы основные понятия,
симметрическими, возвратными и
уравнениями;
связанные с
однородными
рассмотрены основные способы решения рациональных
уравнений;
выявлены приёмы, позволяющие понизить степень
уравнения и тем самым упростить процесс решения;

12.

При работе над темой:
задействовано большое количество математической литературы,
освоение которой, позволило повысить уровень знаний;
изучены различные способы решения квадратных уравнений;
приобретены навыки решения рациональных уравнений, которые в
дальнейшем могут быть использованы при изучении математики в
старших классах и подготовке к математическим олимпиадам и
основному государственному экзамену;