Взаимное расположение прямых в пространстве. Угол между двумя прямыми

1. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ. УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ.

2.

b
а
Пересекающиеся прямые
b
а
Параллельные прямые

3.

C1
AB и A1D1 лежат в
разных плоскостях
D1
B1
A1
C
D
B
A

4.

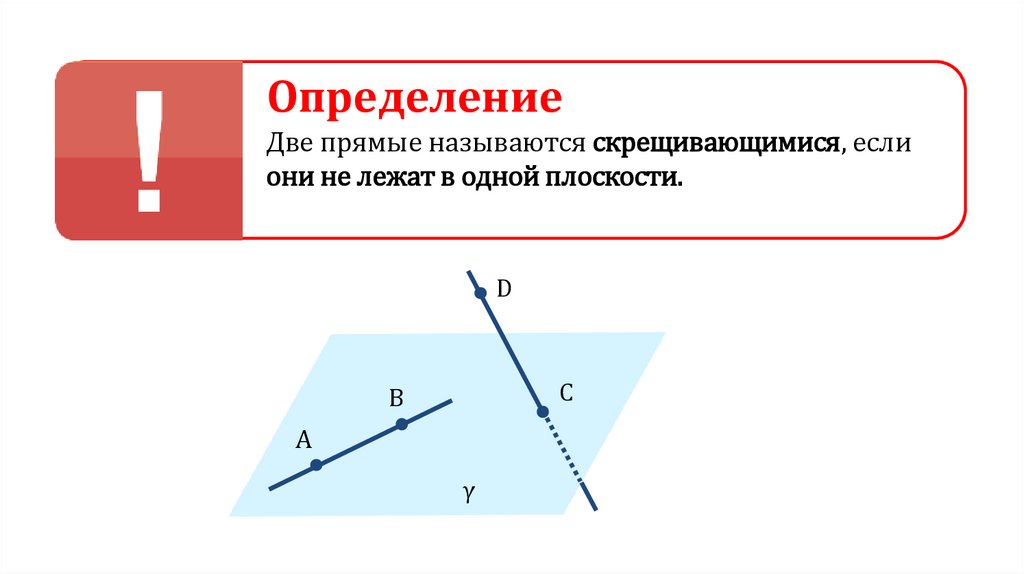
Определение
Две прямые называются скрещивающимися, если
они не лежат в одной плоскости.
D
C
B
A
γ

5.

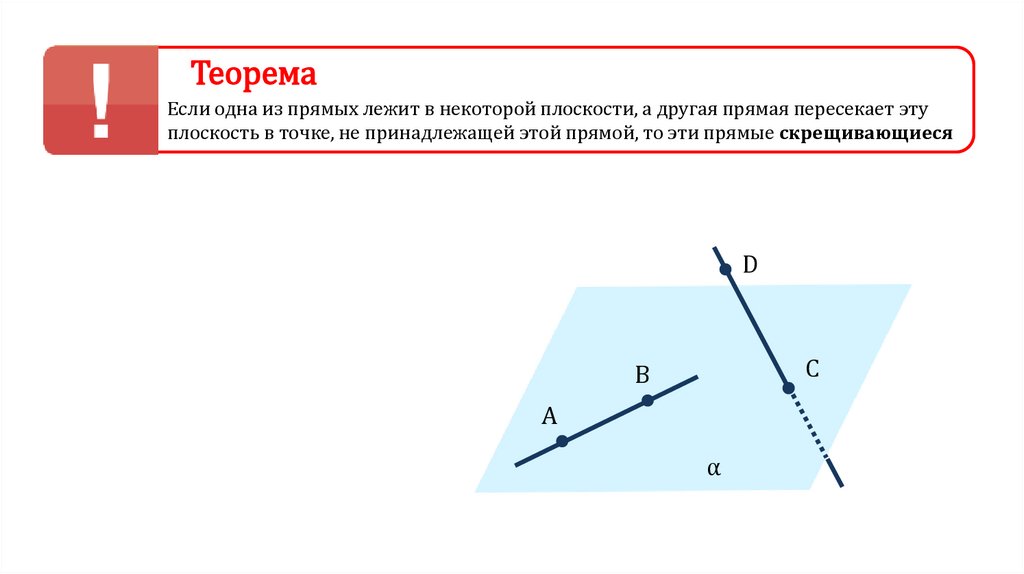
Теорема
Если одна из прямых лежит в некоторой плоскости, а другая прямая пересекает эту
плоскость в точке, не принадлежащей этой прямой, то эти прямые скрещивающиеся
D
C
B
A
α

6.

Теорема
Через каждую из двух скрещивающихся
прямых проходит плоскость,
параллельная другой прямой, и притом
только одна

7.

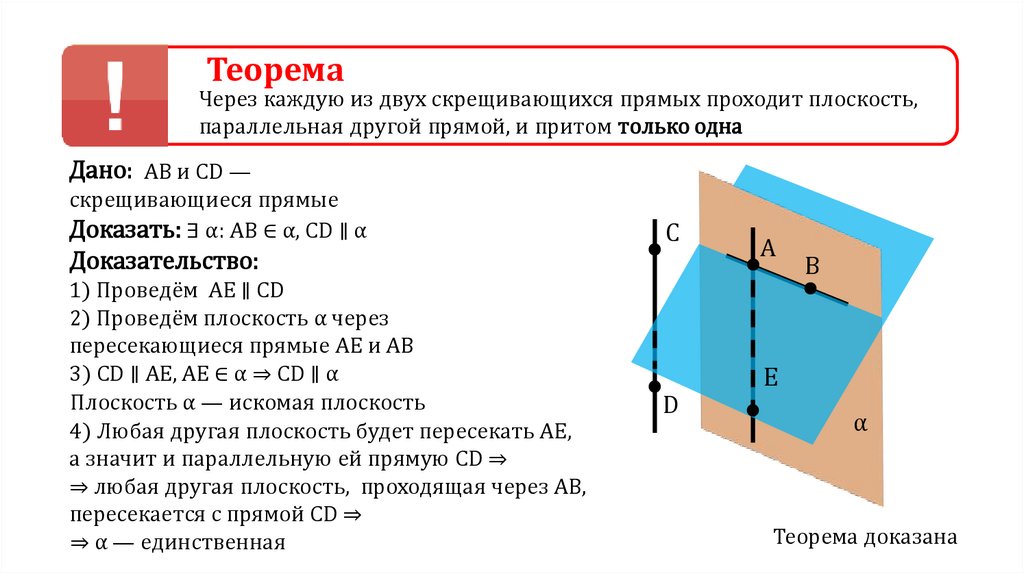
Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость,
параллельная другой прямой, и притом только одна
Дано: АВ и CD —
скрещивающиеся прямые
Доказать: ∃ α: AB ∈ α, CD ∥ α
C
Доказательство:
1) Проведём AE ∥ CD
2) Проведём плоскость α через
пересекающиеся прямые AE и АВ
3) CD ∥ AE, AE ∈ α ⇒ CD ∥ α
Плоскость α — искомая плоскость
4) Любая другая плоскость будет пересекать AE,
а значит и параллельную ей прямую CD ⇒
⇒ любая другая плоскость, проходящая через AB,
пересекается с прямой CD ⇒
⇒ α — единственная
A
B
E
D
α
Теорема доказана

8.

Определение
Любая прямая a, лежащая в плоскости,
разделяет плоскость на две части,
называемые полуплоскостями.
Прямая a называется границей каждой
из этих полуплоскостей

9.

Определение
Два луча ОА и О1А1, не лежащие на одной прямой, называются
сонаправленными, если они параллельны и лежат в одной
полуплоскости с границей ОО1.
Два луча ОА и О1А1, лежащие на одной прямой называются
сонаправленными, если они совпадают или один из них
содержит другой.

10.

Сонаправленные лучи
A
O
A1
O
O1
O1
A
A1

11.

Теорема
Если стороны двух углов
соответственно сонаправлены,
то такие углы равны

12.

α — угол между прямыми
a
b
α
a
b
∠α
180˚ – α
0˚ < α < 90˚
∠α = 90˚

13.

Угол между
скрещивающимися прямыми
A
A1
D1
D
C
C1
K1
B1
B

14.

A2
A
A’
D2
C2
A1
D1
D
K2
C
B2
K’
C1
K1
B1
B
A₁B₁ ∥ A₂B₂ ∥ A’B’
C₁D₁ ∥ C₂D₂
B’
⇒ ∠A’K’D = ∠A₁K₁D₁ = ∠A₂K₂D₂

15.

A2
A
A’
D2
C2
A1
D1
D
K2
C
B2
K’
C1
K1
B1
B
B’
Величина угла между скрещивающимися
прямыми от выбора точки не зависит