Координаты вектора

1.

2.

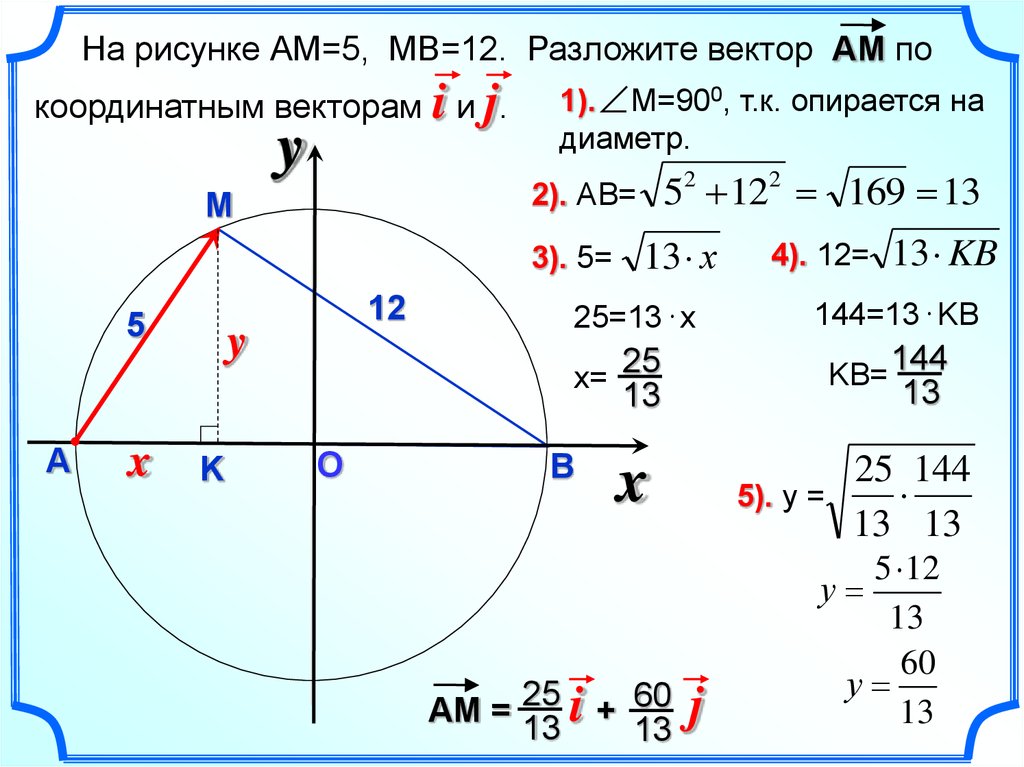
На рисунке АМ=5, МВ=12. Разложите вектор АМ по
координатным векторам i и j.
y
1). М=900, т.к. опирается на
диаметр.
M
3). 5=
5
52 122 169 13
2). АВ=
12
y
13 х
25=13 x
x
K
О
В
144=13 KB
13
25 144
5). y =
13 13
x
АМ = 25 i + 60
13
13
13 KB
KB= 144
x= 25
13
А
4). 12=
j
5 12
у
13
60
у
13

3.

Север
Запад
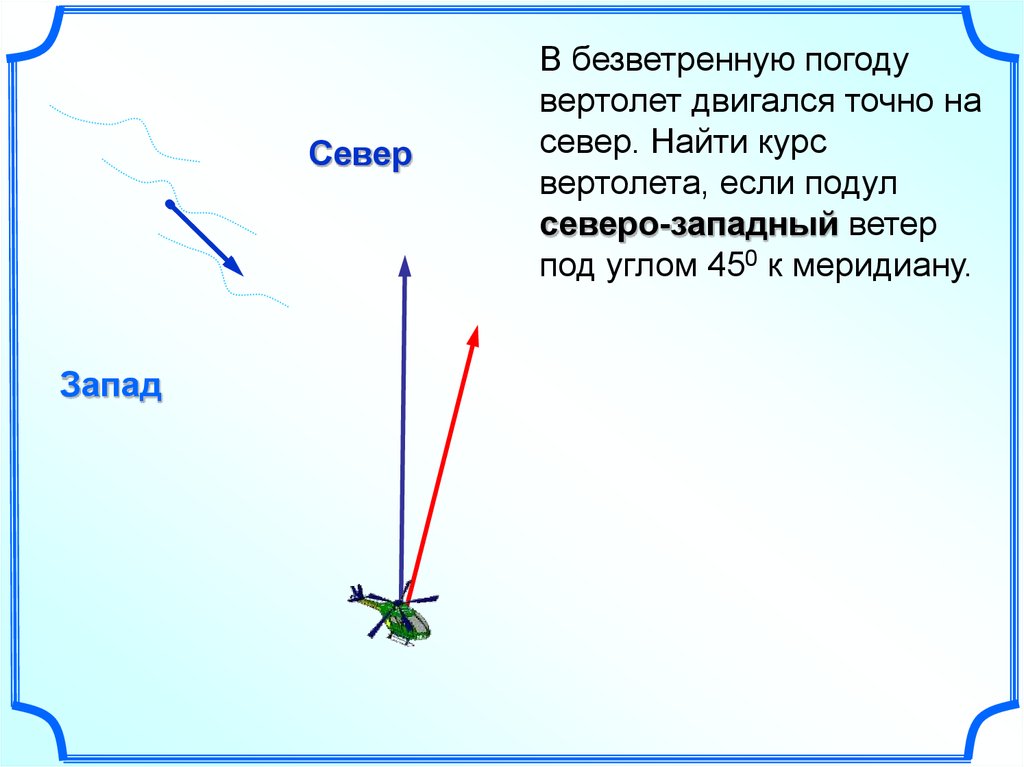
В безветренную погоду
вертолет двигался точно на
север. Найти курс
вертолета, если подул
северо-западный ветер
под углом 450 к меридиану.

4.

10
Каждая координата суммы двух или более
векторов равна сумме соответствующих
координат этих векторов.
Рассмотрим векторы
a {x1; y1}
a = x11i +y11 j
a+b =
b {x2; y2}
и
b+
= x2i +y2 j
=
= (x1+ x2)i + (y1 + y2 ) j
a +b {x1+x2; y1+y2}

5.

Найдите координаты вектора
a {-6; 9}
+
n {-8; 0}
a +n {-14;9}
s {-6; -4}
+
p { 2; 1}
s +p {-4;-3}
№ 922
a {3; 2}; b {2; 5}
a +b { 5; 7}
a {3;-4}; b {1; 5}
a +b { 4; 1}
a {-4;-2}; b {5; 3}
a +b { 1; 1}
a {2; 7}; b {-3;-7}
a +b {-1; 0}

6.

20
Каждая координата разности двух векторов
равна разности соответствующих координат
этих векторов.
Рассмотрим векторы
a {x1; y1}
b –= x22i +y22 j
a = x11i +y11 j
a–b =
(
b {x2; y2}
и
)=
= (x1– x2)i + (y1 – y2) j
a–b {x1–x2; y1–y2}

7.

30
Каждая координата произведения вектора на
число равна произведению соответствующей
координаты вектора на это число.
Рассмотрим вектор
a = xi +y j
a {x; y}
k
ka = kxi +ky j
ka {kx; ky}
a {-2; 1} 3
3a {-6; 3}
a {-2; 0} (-2)
-2a {4; 0}
a {-2; 5} (-1)
-a {2; -5}

8.

a-b
b {-8;12}
Найдите координаты вектора
a {-6; 9}
1 способ
2 способ
(-1)
a - b {2;-3}
-b{8;-12}
+
a - b {2;-3}

9.

№923 Найдите координаты вектора
1)
a - b, если
a {5;3}; b {2;1}
1 способ
a {5; 3}
b {2; 1}
a - b {3; 2}
2 способ
b {2; 1} (-1)
a {5; 3}
+
-b{-2;-1}
a - b {3; 2}

10.

Найти координаты векторов.
a {2; 4}; 3a{
}
b{-2; 0}; -2b{
}
d{-2;-3}; -3d{
}
c {2;-5}; -c{
}
e {2;-3}; 0,5e{
}
-2f{
}
f(0; 5};
Проверить.
Вводите ответы в текстовые поля, не делая пробелов

11.

Найти координаты векторов,
противоположных данным.
a {2; 4}; -a{
}
b{-2; 0}; -b{
}
d{-2;-3}; -d{
}
c {0; 0}; -c{
}
e {2;-3}; -e{
}
-f{
}
f(0; 5};
Проверить.
Вводите ответы в текстовые поля, не делая пробелов

12.

Найти координаты векторов.
a {2; 4}; c {3; 2}; a +c {
}
b{-2; 0}; d{-2;-3};
b+d{
}
c {2;-5}; e {2;-3};
c +e{
}
f(0; 5}; d{-2;-3};
f - d{
}
b{-2; 0}; d{-2;-3};
b - d{
}
a {2; 4}; c {3; 2};
a - c{
}
Проверить.
Вводите ответы в текстовые поля, не делая пробелов

13.

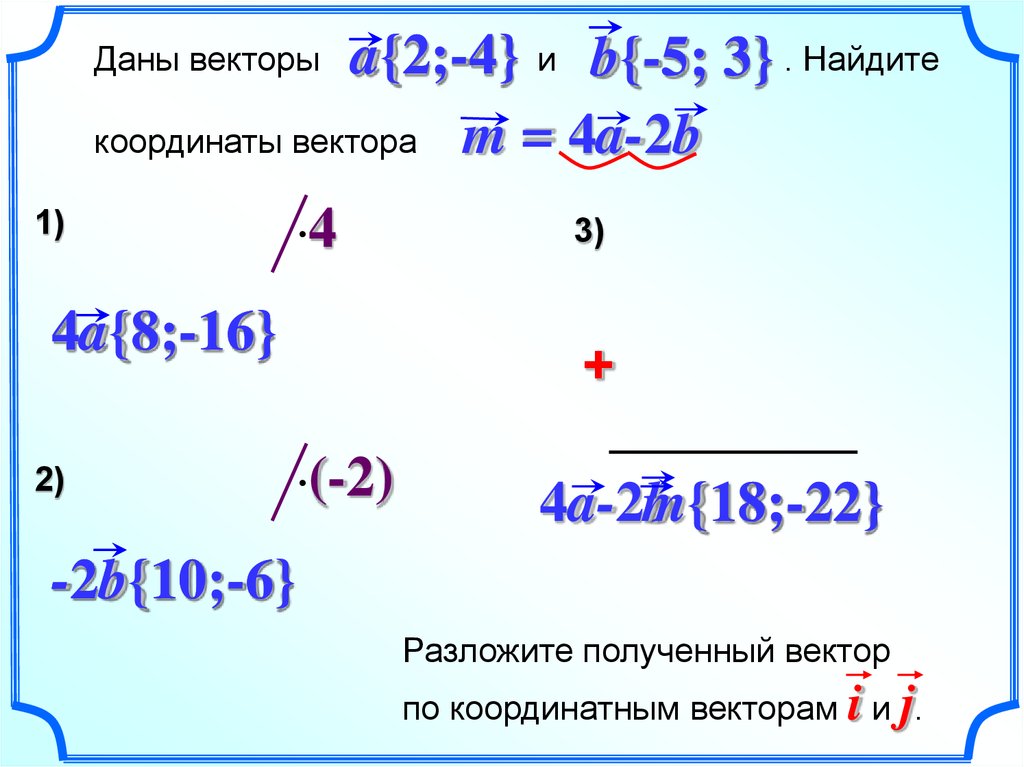
a{2;-4} и b{-5; 3} . Найдите
координаты вектора m = 4a-2b
Даны векторы
1)
4
4a{8;-16}
2)
3)
+
(-2)
4a-2b
m{18;-22}
{18;-22}
-2b{10;-6}
Разложите полученный вектор
по координатным векторам i и j.

14.

a{2;-4} и b{-5; 3} . Найдите
n = 3a-4b
координаты вектора
Даны векторы
1)
3
3a{6;-12}
2)
3)
+
(-4)
3a-4bn{26;-24}
{26;-24}
-4b{20;-12}
Разложите полученный вектор
по координатным векторам i и j.

15.

a{-7;-1} b{-1; 7} c{4;-6}
1
–
Найдите координаты вектора v = 3a –2b
c
2
1)
3
4)
3a{-21;-3}
+
Даны векторы
(-2)
2)
-2b{2;-14}
(– 12)
3)
– 1 c{-2;
2
v{-21;-14}
3}
№926(в)
Разложите полученный вектор
по координатным векторам i и j.

16.

a{-4; 8}; b{-3;-2};
Найти координаты векторов.
a + b {-7; 6}
a – b {-1;10}
-a {4;-8}
2a {-8;16}
-3b { 9; 6}
2a – 3b { 1; 22}

17.

a{-2; 6}; b{5;-2};
c {4;-2}; e {2;10};
Найти координаты векторов.
}
c+e {
}
}
e–c {
}
-a {
}
-e {
}
2a {
}
3c {
}
-3b {
}
-2e {
}
2a – 3b {
}
3c – 2e {
}
a+b {
a–b {

18.

y
А
N
О
Дано: AOB – равносторонний, ОА= a
М и N – середины сторон OA и AB.
Разложите векторы ОМ и BN
по координатным векторам i и j.
M
x
a
В
Способы решения
Завершить показ

19.

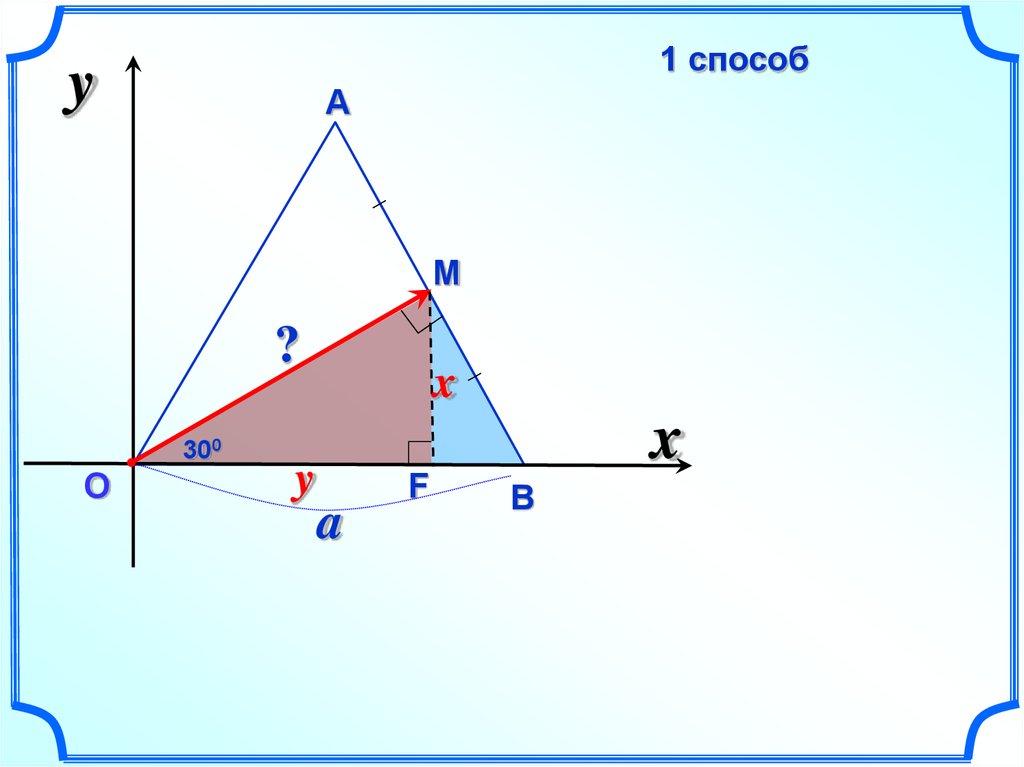
1 способ
y
А
M
?
300
О
y
x
x
a
F
В

20.

y
2 способ
a
А
2
D
M
Z
x
300
О
y
a
F
В
x

21.

y
А
N
О
M
a
В
x
К началу задачи