Похожие презентации:
Спин, два электрона
1.
ЗадачаИмеются две невзаимодействущие частицы, каждая из которых обладает спином s=1/2. Одна из
этих частиц обладает определённой проекцией спина на ось Oz, а вторая – на направление
n sin cos ,sin sin ,cos
Измеряются полный спин S и проекция полного спина на ось Oz. Найти вероятности
измерения возможных значений указанных величин.
z
n
s1z s
2n
x
Оператор полного спина и проекции полного спина
ˆ
S sˆ1 sˆ2 , Sˆz sˆ1z sˆ2 z
y
2.
Два набора квантовых чисел, описывающих возможные состояния системыI : s1 , s2 , s1z , s2 z
II : s1 , s2 , S , S z
s1 1/ 2, s2 1/ 2, s1z , s2 z s1z , s2 z s1z
1 1
1 1
, , ,
2 2
2 2
1 1
1 1
, , ,
2 2
2 2
1
s2 z
2
Sz 0
S z 1
s1 1/ 2, s2 1/ 2, S , S z S , S z
0,0 , 1,0
1,1 , 1, 1
Идея решения – находим матрицу перехода от состояний из набора I к состояниям из набора II.
Затем находим обратную матрицу и используя её раскладываем состояние
s1z 1/ 2, s2 n 1/ 2
по базису
S , Sz
3.
Матрица перехода от состояний из набора I к состояниям из набора II.Решение в обозначениях Дирака
Принцип суперпозиции
SS z
SS z
C
s1 z s2 z s1 z s2 z
s1 z s2 z
Матрица перехода (унитарное преобразование от одного представления к другому)
CsSS1z sz2 z s1z s2 z SS z
4.
Кет-векторы в матричном представлении1 1
1
,
2 2
2
1
1 1
1
,
2 2
2
1
2
1
1
2
1 1
1
, ,
2 2
2
2
1 1
1
, ,
2 2
2
2
1
1
2
1 0 0 1
,
0 1 1 2 1 1 0 2
2
1
2
1 1 0 0
,
0 1 0 2 1 1 1 2
2
1
5.
ОбозначенияВ дальнейшем для краткости будем использовать обозначение
1 0
1 1
1 1
, ssz ,
2 2
2 2
0 1 1 2
6.
Матрицы понижающих операторов в представлении s1s1 z s2 s2 z0 0
sˆi
1 0 i
0
0
0
0
ˆ
S sˆ1 sˆ2
1 0 1 1 0 2
7.
Состояние с максимальными значения квантовых чиселS 1, S z 1
11
C
s1 z s2 z s1 z s2 z s1z 1/ 2, s2 z 1/ 2
s1 z s2 z
Действуем на левую часть понижающим оператором
Sˆ S 1, S z 1 ?
Найти результат действия, используя общую формулу
ˆj jjz ( j jz )( j jz 1) jjz 1
8.
Результатˆj jjz ( j jz )( j jz 1) jjz 1
ˆj Sˆ , j S 1, jz S z 1
Sˆ S 1, S z 1 2 S 1, S z 0
Теперь действуем суммой понижающих операторов на правую часть
1
Sˆ S 1, S z s sˆ1 sˆ2 Cs111 z s2 z s1 z s2 z sˆ1 sˆ2
2
s1 z s2 z
Результат действия?
1
1
2
2
9.
Результат действия?sˆ1 sˆ2
1
2
1
1
2
0 0 0 0 1 1
2
1 0 1 1 0 2 0 1 0 2
10.
Результат действия1
ˆ
S S 1, S z 1 2 S 1, S z 0 sˆ1 sˆ2
2
1
1
2
2
0 0 0 0 1 1 0 1 1 0
1 0 1 1 0 2 0 1 0 2 1 1 0 2 0 1 1 2
Или
1 0 1 1 0 1 1
S 1, S z 0
2 1 1 0 2 0 1 1 2
2 2
Найти кет-вектор
S 0, S z 0 ?
1
1
2
1
2
2
1
1
2 2
11.
Кет-вектор с разными квантовыми числами ортогональны друг другу (вырождения нет)S 1, S z 0 S 0, S z 0 0
Найти результат?
12.
Промежуточные формулы0 1
1 0
S 0, S z 0 A B
1 1 0 2
0 1 1 2
0 1
1 0
1
S 1, S z 0 S 0, S z 0
01 1 1 0 2 1 0 1 01 2 A B
2
0 1 1 2
1 1 0 2
13.
Результат1 0 1 1 0 1 1
S 0, S z 0
2 1 1 0 2 0 1 1 2
2 2
1
1
2
2
1
2
1
1
2 2
14.
Собираем все результаты вместеS 1, S z 1
1
2
1
S 1, S z 1
1
2
1
2
2
1
1
2
1 1
S 1, S z 0
2 2
S 0, S z 0
1 1
2 2
2
1
1
2
1
2
2
1
1
2
2
1
2
1
1
2 2
1
1
2 2
15.
Фазы кет-векторов с разным полным моментомОтносительные фазы кет-векторов с одинаковым полным моментом
S 1, S z 0, 1
определены!
Вопрос: как определить относительные фазы векторов с разными полными моментами?
Например
S 1, S z 0
and
S 0, S z 0
Ответ из теории коэффициентов Клебша-Гордана
Два представления
j1 j2 JJ z , J z j1z j2 z
j1 j2 j1z j2 z
Правило (Мессиа, Квантовая механика, том 2)
j1, j2 , j1z j1 , j2 z J z j1 j1 j2 JJ z J 0
Определить «абсолютные» фазы векторов
S 1, S z 0, 1
and
S 0, S z 0
16.
«Абсолютные» фазы кет-векторовКет-векторы в рассматриваемой задаче
1
1
ei
1
1
1
1
j1 , j2 , J 0, J z 0 S 0, S z 0
j1z , j2 z
j1z , j2 z
2
2
2
2
2
2
2
1
1
1
1
j1 , j2 , j1z j1 , j2 z J z j1 j1z , j2 z
2
2
2
2
Правильная «абсолютная» фаза
j1 , j2 , j1z j1 , j2 z J z j1 j1 j2 JJ z J
ei
1
1
1
1
1
1
1
1
j1z , j2 z j1z , j2 z
j1z , j2 z j1z , j2 z
2
2
2
2
2
2
2
2
2
Или
ei
j1 , j2 , j1z j1 , j2 z J z j1 j1 j2 JJ z J
0 ei 1,
2
17.
Окончательный вид разложенияS 1, S z 1
1
2
1
S 1, S z 1
1
2
1
2
2
1
1
2
1 1
S 1, S z 0
2 2
S 0, S z 0
1
1 1
2 2
2
1
2
1
1
2
2
1
2
2
1
1
2
1
2 2
1
1
2 2
18.
Построить матрицу преобразованияS
S
S
S
1, S z 1
1, S z 0
ˆ
M
1, S z 1
0, S z 0
1
2
1
1
2
1
2
1
2
1
2
1
2
1
2
1
2 2
1
1
2 2
1
2
19.
Матрица преобразования1
ˆ
M
2
2
0
0
0
0
1 0 1
0 2 0
1 0 1
0 0
Проверить на унитарность
ˆ ˆ † ?
MM
Выразить кет-векторы из второго набора квантовых чисел через кет-векторы первого набора?
20.
Результат1
2
1
1
2
1
2
1
2
1
2
2
1
1 0
1 2 2
2 0
1
0
2 2
1
1
2 2
1
2
0
1 0
1
0 2 0
1 0
1
0 0
S 1, S z 1
S 1, S z 0
S 1, S z 1
S 0, S z 0
21.
Кет-вектор исходного состоянияcos
1
1
2
s1z 1/ 2, s2 n 1/ 2
cos
2 2
0 1 sin ei
2
2
1
1
2
1
sin e
2
2
2
i
1
1
2
Выразить кет-векторы из второго набора квантовых чисел через кет-векторы первого набора?
2
22.
Результатei
ei
s1z 1/ 2, s2 n 1/ 2 cos 11
sin 10
sin 00
2
2
2
2
2
Вероятности
1
2
w S 1, S z 1 cos , w S 1, S z 0 w S 0, S z 0 sin
2
2
2
2








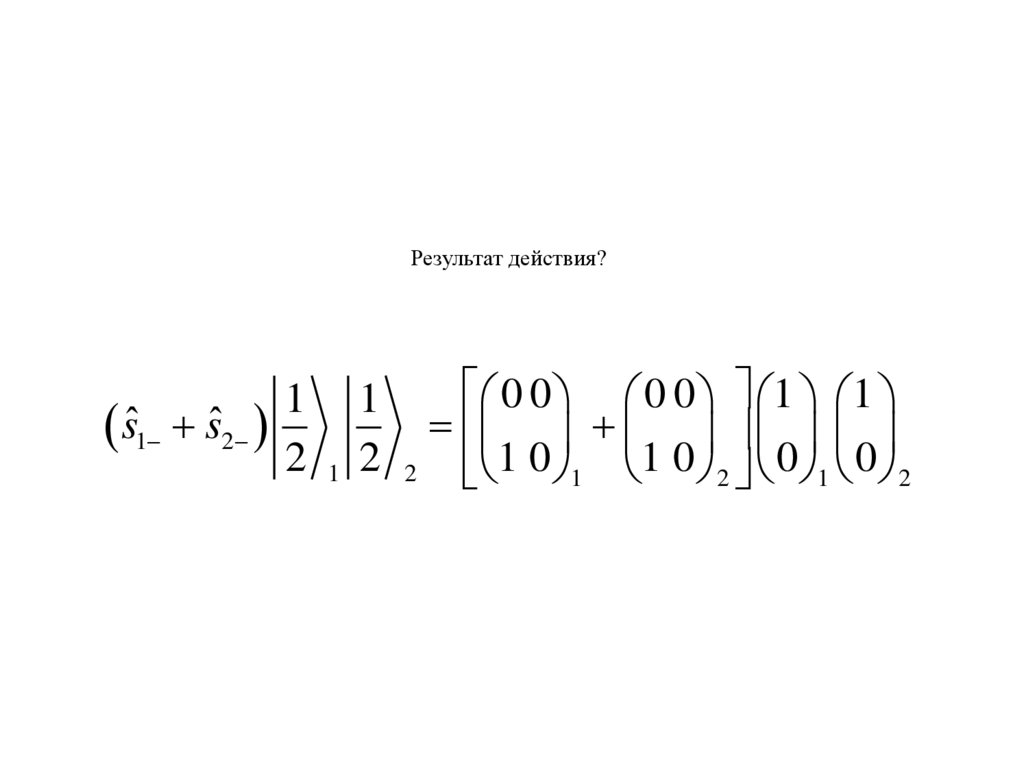













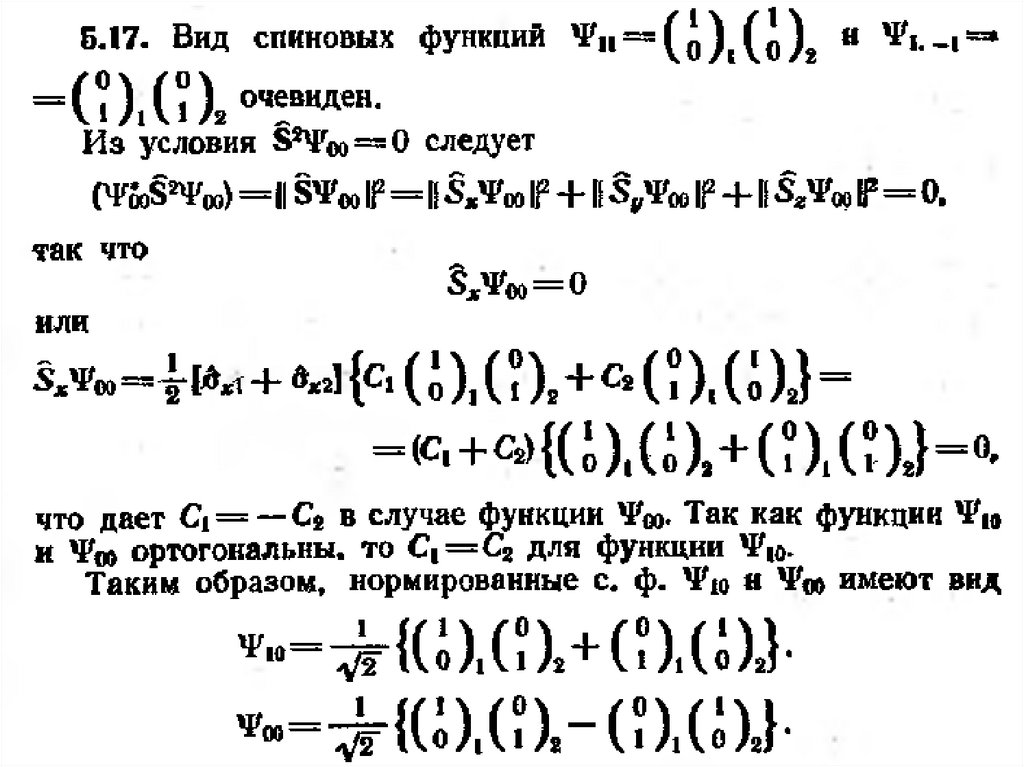
 Физика
Физика








