Похожие презентации:
Электрические поля при наличии поверхностей раздела диэлектрических сред
1.
Методическая разработкана тему:
«Электрические поля при наличии
поверхностей раздела
диэлектрических сред»
курс «Методика и технологии
подготовки обучающихся к участию
во всероссийских олимпиадах по
математике, физике и астрономии»
Слушатель Анциферова О.Н.
2.
Задача № 1• Плоский воздушный конденсатор представляет
собой две квадратные металлические пластины
размерами a×a, расположенные на расстоянии
d друг от друга, причем d≪a. Заряженный
конденсатор помещают в широкий сосуд с
непроводящей жидкостью так, что пластины
вертикальны и их нижние края находятся на
уровне поверхности жидкости. Жидкость
поднимается между пластинами и
устанавливается на высоте h<a.
3.
• Почему это происходит?• Каким станет напряжение U
между пластинами?
Поверхностным натяжением
можно пренебречь. Плотность
жидкости ρ, диэлектрическая
проницаемость ϵ.
4.
Решение:• Как известно, диэлектрик втягивается в область
более сильного электрического поля, а у края
конденсатора возникает как раз резко
неоднородное поле. Однако непосредственное
вычисление силы, действующей на жидкость со
стороны неоднородного поля, — непростая
задача. Поэтому применим «энергетический
подход»: воспользуемся тем, что потенциальная
энергия Wp системы в положении устойчивого
равновесия минимальна.
5.
• Эта энергия складывается изпотенциальной энергии mgh/2
столбика втянутой в конденсатор
жидкости (высота ее центра
тяжести h/2) и энергии поля
заряженного конденсатора q2/2C.
6.
• Заряд q конденсатора остается приподъеме жидкости неизменным, а емкость
конденсатора возрастает
2/
a d
C0=ϵ0
до C=(ϵ0a2/d)(1+(ϵ−1)h/a)
от
7.
Учитывая, что m=ρdah,
записываем:
Wp=ρgdah2/2+q2d/(2ϵ0a(1+(ϵ−1)h))
8.
Приравнивая нулюпроизводную Wp по h, получаем
ρgdah−q2d(ϵ−1)/(2ϵ0a(a+(ϵ−1)h)2)=0
9.
Поскольку q=CU,находим U=d 2ρgh
ϵ0(ϵ−1)
10.
Ответ:U=d 2ρgh
ϵ0(ϵ−1)
11.
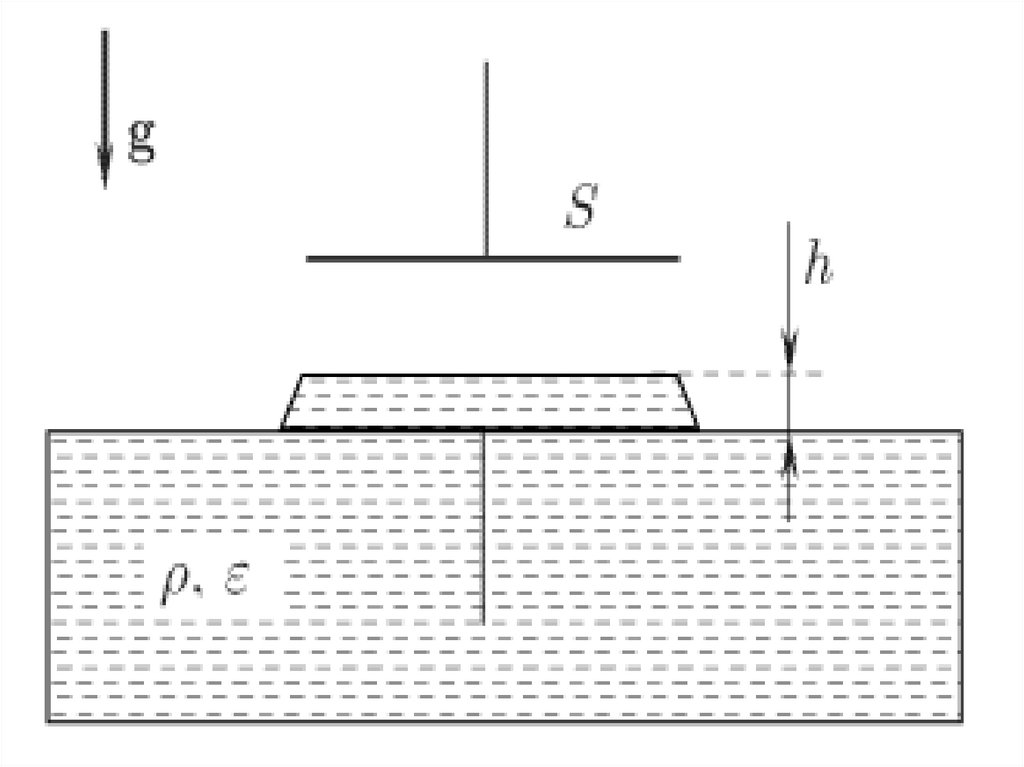
Задача № 2Одна из пластин плоского конденсатора
сделана из проводящей сетки и лежит на
поверхности жидкого диэлектрика с
диэлектрической проницаемостью ϵ и
плотностью ρ (см. рис.). На какую высоту h
поднимется диэлектрик в конденсаторе,
если сообщить конденсатору заряд q?
Площадь пластин конденсатора равна S.
12.
13.
Решение:Напряженность электрического поля в
конденсаторе в области, где нет диэлектрика,
определяется соотношением E0=q/(ϵ0S) в
области с диэлектриком — E=q/(ϵ0ϵS). Найдем
изменение энергии конденсатора при подъеме
диэлектрика на высоту h, воспользовавшись
формулой для плотности энергии
электрического поля w=(1/2)ϵϵ0E2.
14.
Получаем:2
ΔW=W−W0=(q h/(2ϵ0S))(1/ϵ−1).
Изменение энергии отрицательно, т. е.
при подъеме диэлектрика
потенциальная энергия электрического
поля конденсатора, а значит и энергия
самого конденсатора уменьшается.
Изменение энергии Δ
W равно работе
электрической силы, взятой с обратным
знаком.
15.
Поскольку ΔW пропорционально
высоте подъема диэлектрика h, то
электрическая сила Fэл постоянна:
2
Fэл=q (ϵ−1)/2ϵϵ0S
16.
Для определения высоты подъемажидкости h приравняем силу
тяжести и электрическую силу,
действующие на втянутый внутрь
конденсатора диэлектрик:
2
Shρg=q (ϵ−1)/2ϵϵ
S
0
17.
откуда искомая высотаподъема равна
2
2
h=q (ϵ−1)/2ϵϵ0S ρg
18.
Если заряженный конденсатор положить наповерхность жидкого диэлектрика, то
жидкость, втягиваясь в конденсатор,
приобретет не только потенциальную энергию,
но и кинетическую и возникнут колебания
около положения равновесия. Эти колебания
постепенно затухнут из-за вязкости жидкости.
Чтобы избежать колебаний жидкости, нужно
лежащий на поверхности конденсатор
заряжать медленно, например, плавно
увеличивая подаваемое на него напряжение.
19.
Ответ:2
2
h=q (ϵ−1)/2ϵϵ0S ρg
20.
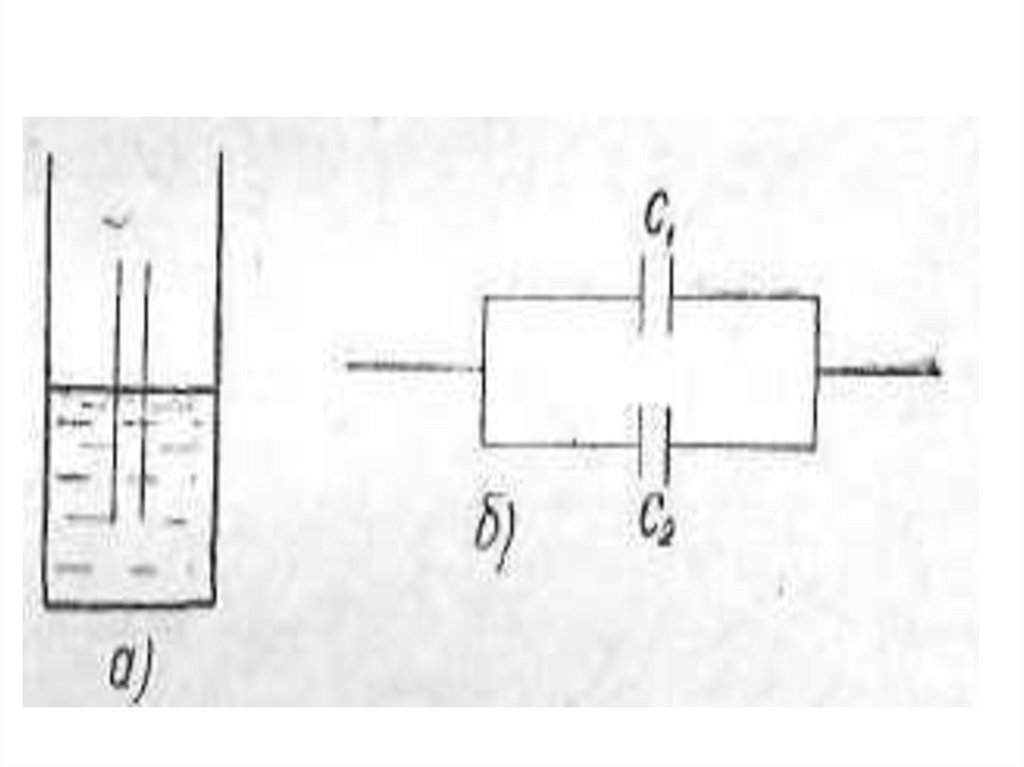
Задача № 3Плоский конденсатор, у которого
расстояние между пластинами равно
4 мм, погружается до половины в
керосин (рис. а). Диэлектрическая
проницаемость керосина — 2. На
сколько нужно раздвинуть пластины
конденсатора, чтобы его емкость
осталась неизменной?
21.
22.
Решение:Емкость параллельно соединенных
конденсаторов равна сумме их емкостей
(рис. б). До погружения в керосин емкость
конденсатора была равной C=ϵBϵ0S/d, где
ϵ0=1/4π⋅9⋅109ф/м— постоянный
коэффициент, называемый
диэлектрической проницаемостью
вакуума; ϵB — диэлектрическая
проницаемость воздуха, равная единице.
23.
После погружения конденсатора дополовины в керосин и раз-движепия
пластин до некоторой величины d1
образовались два параллельно
соединенных конденсатора с площадью
пластин S/2 у каждого. Вычислим емкость
образовавшегося сложного
конденсатора, пользуясь формулой для
двух конденсаторов, соединенных
параллельно, и приравняем ее к
первоначальной емкости конденсатора:
24.
C=C1+C2=ϵBϵ0S/2d1+ϵKϵ0S/2d1.
25.
Подставим вместо C его значениеϵBϵ0S/d=ϵBϵ0S/2d1+ϵKϵ0S/2d1
Откуда
d1=3/2*d=6мм
Δd=d1−d=2мм.
26.
Задача № 4Одна пластина конденсатора закреплена
неподвижно на дне широкого сосуда с жидким
диэлектриком (диэлектрическая проницаемость его
ϵ, плотность ρ). Вторая, имеющая вид бруска высотой
H, плавает над ней, погрузившись на 1/4 своего
объема, если пластины не заряжены. Какую разность
потенциалов надо приложить к пластинам, чтобы
верхняя пластина погрузилась наполовину?
Первоначальное расстояние между пластинами
конденсатора H. Поле между пластинами считать
однородным.
27.
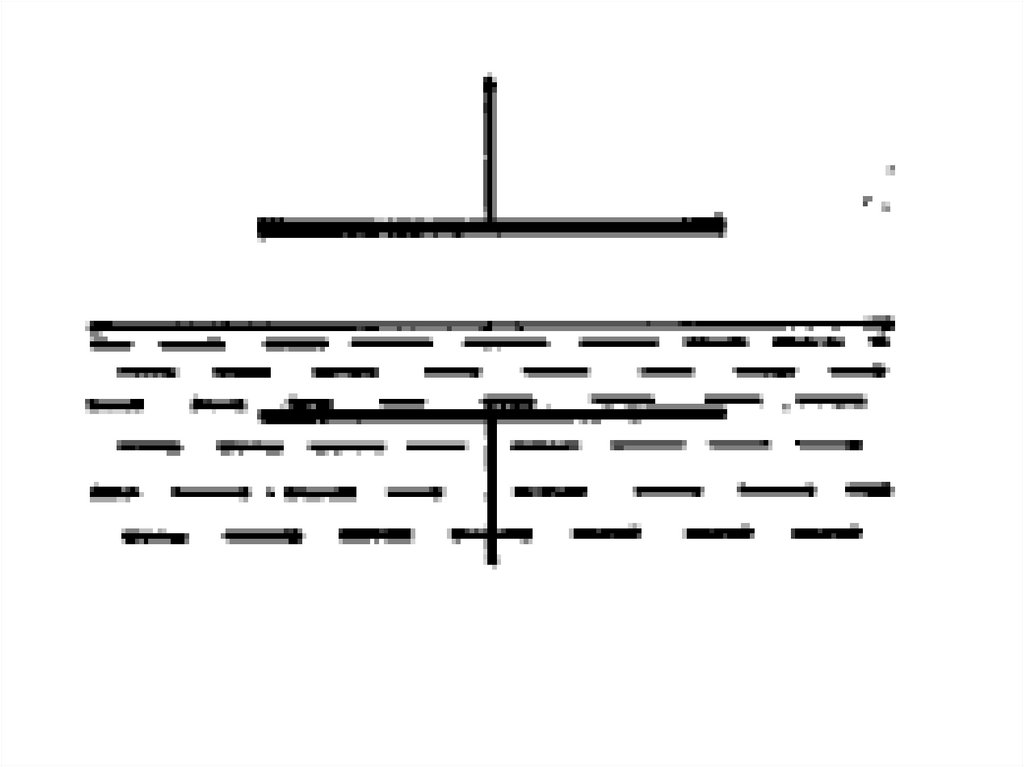
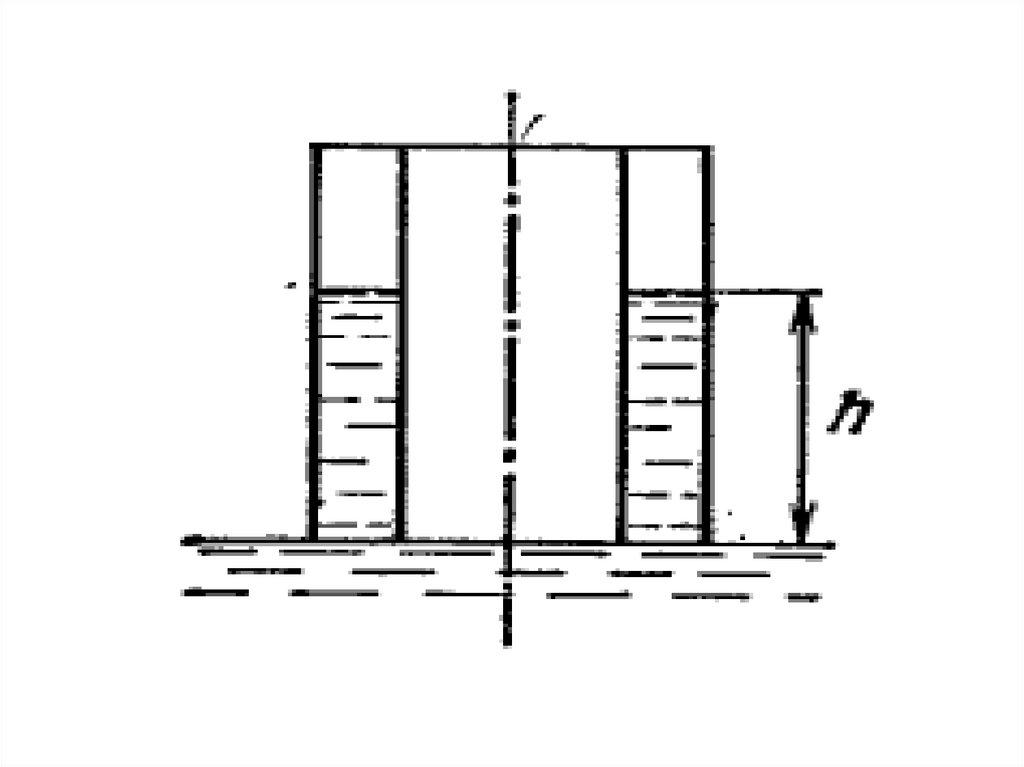
Задача № 5Плоский конденсатор расположен горизонтально
так, что одна его пластина находится над
поверхностью жидкости, другая — под
поверхностью жидкости (рис.). Диэлектрическая
проницаемость жидкости ϵ, ее плотность ρ. На
какую высоту поднимется уровень жидкости в
конденсаторе после сообщения его пластинам
заряда с поверхностной плотностью σ?
28.
29.
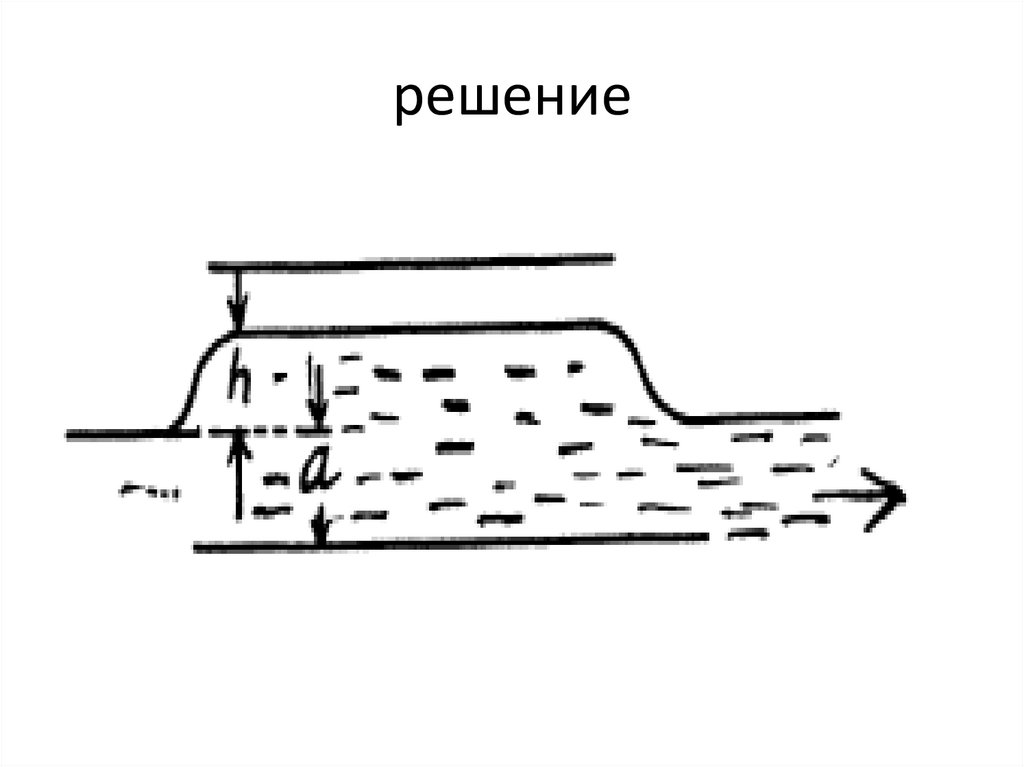
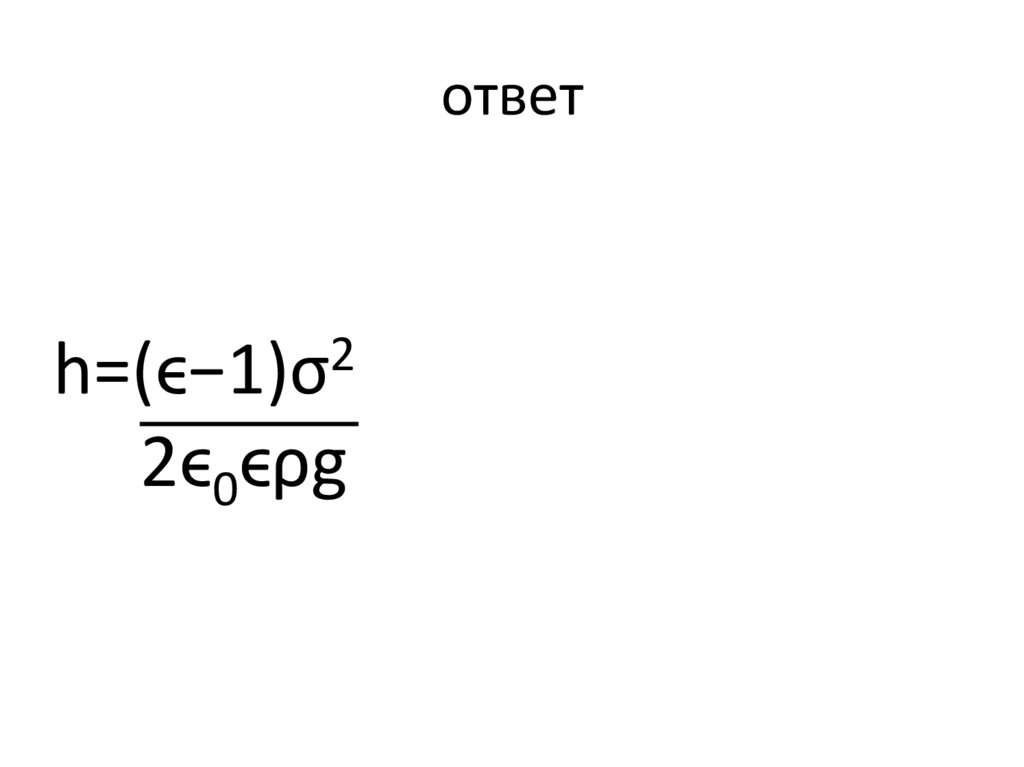
решение30.
Один из способов решения этой проблемыбудет таким же, как и в случае задачи № 2 ,
поэтому можно попробовать альтернативный
метод, основанный на энергии. Пусть жидкость
поднимается на расстояние h. Затем вычислим
дополнительную энергию жидкости как сумму
энергии поляризации и обычной
гравитационной энергии. Последнее дает
1/2h⋅ρg⋅Sh=1/2ρgSh2
31.
ответ2
h=(ϵ−1)σ
2ϵ0ϵρg
32.
Задача № 6Цилиндрический конденсатор, подключенный к
источнику постоянного напряжения U, упирается
своим торцом в поверхность воды (рис.). Расстояние
d между обкладками конденсатора значительно
меньше их среднего радиуса. Найти высоту h, на
которой установится уровень воды между
обкладками конденсатора. Капиллярными
явлениями пренебречь.
33.
34.
ответВ равновесии они должны быть в балансе;
ρgdh=ϵ0(ϵ−1)V2/2d
следовательно h=ϵ0(ϵ−1)V2/2ρgd2








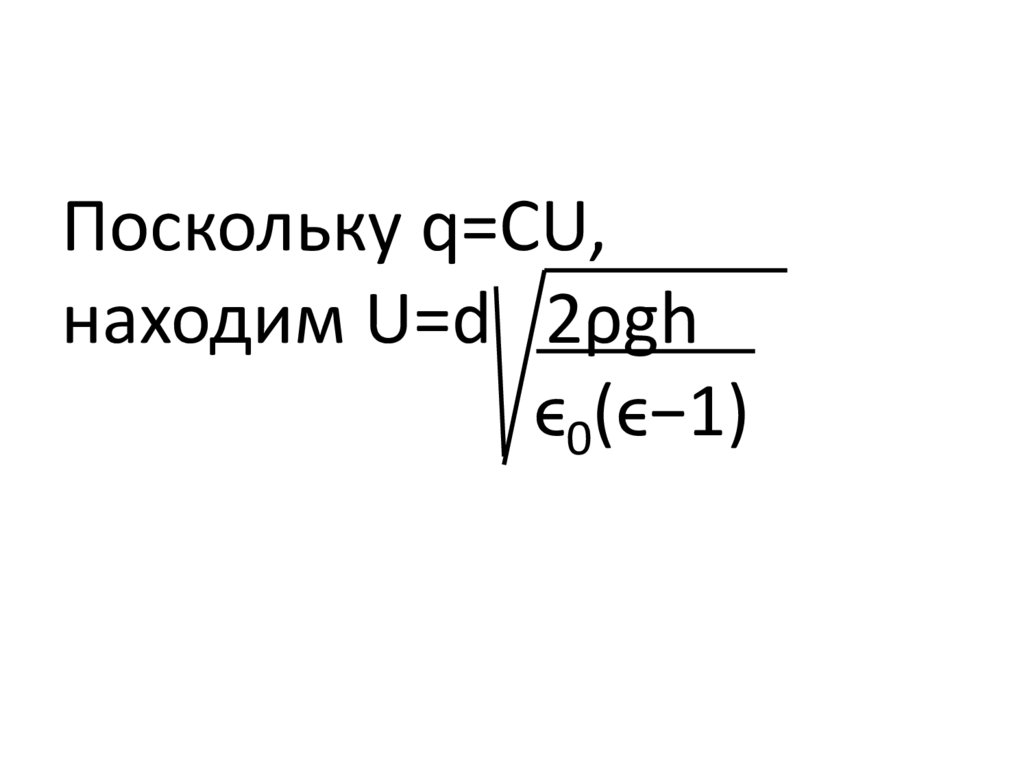
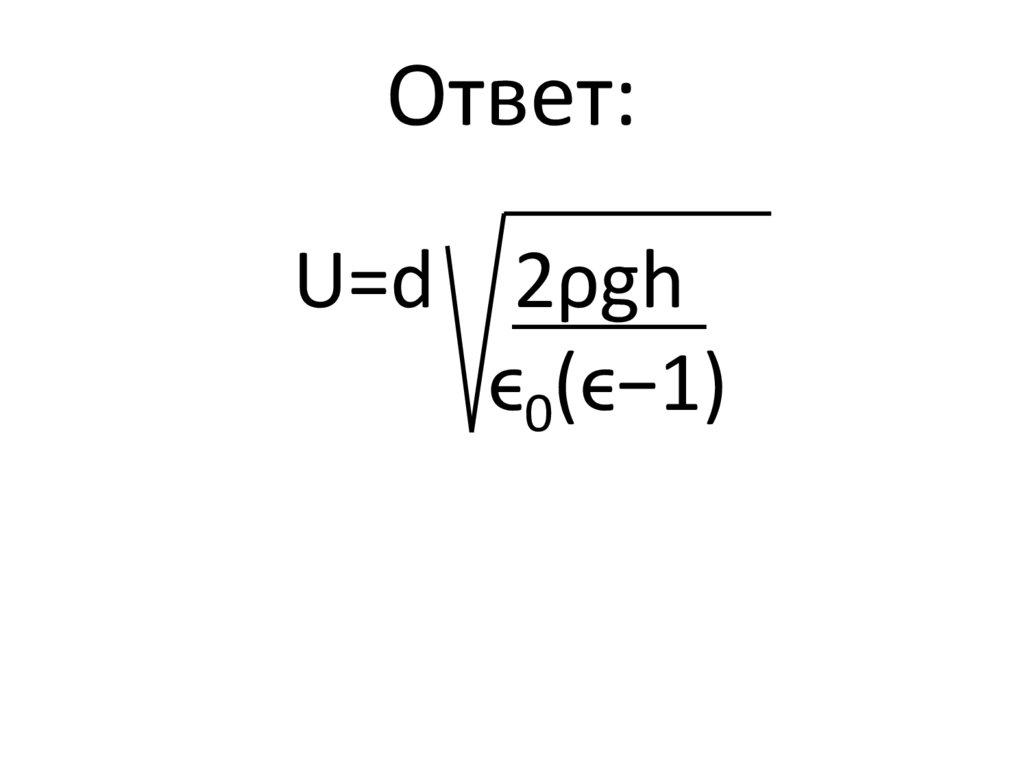







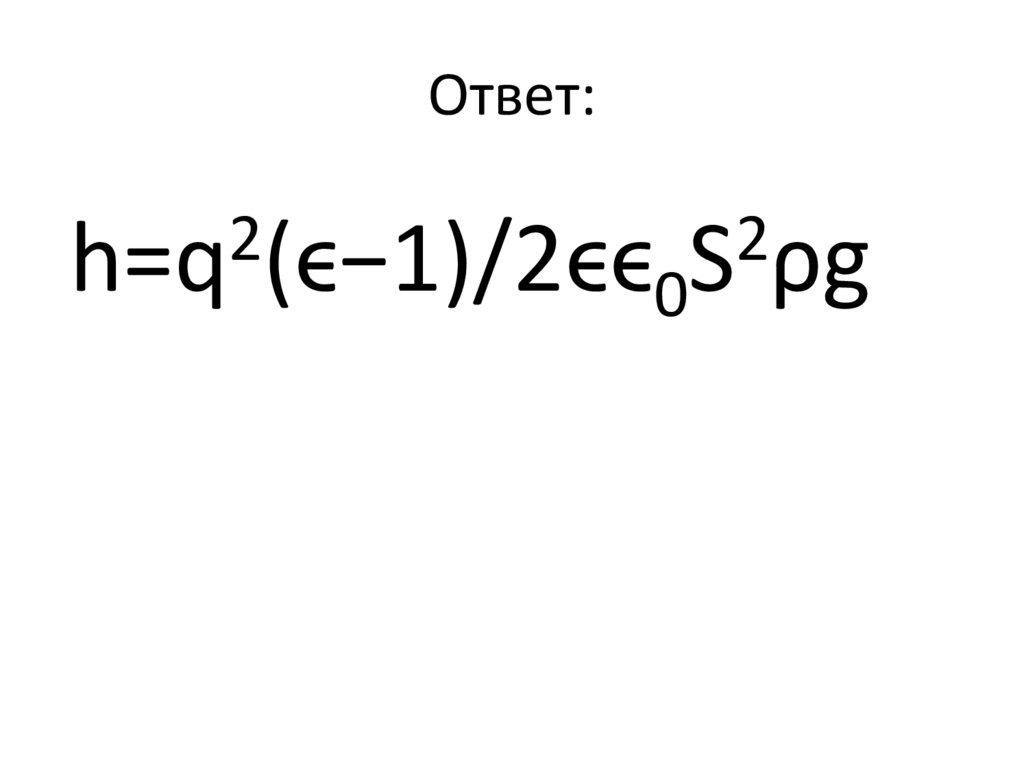



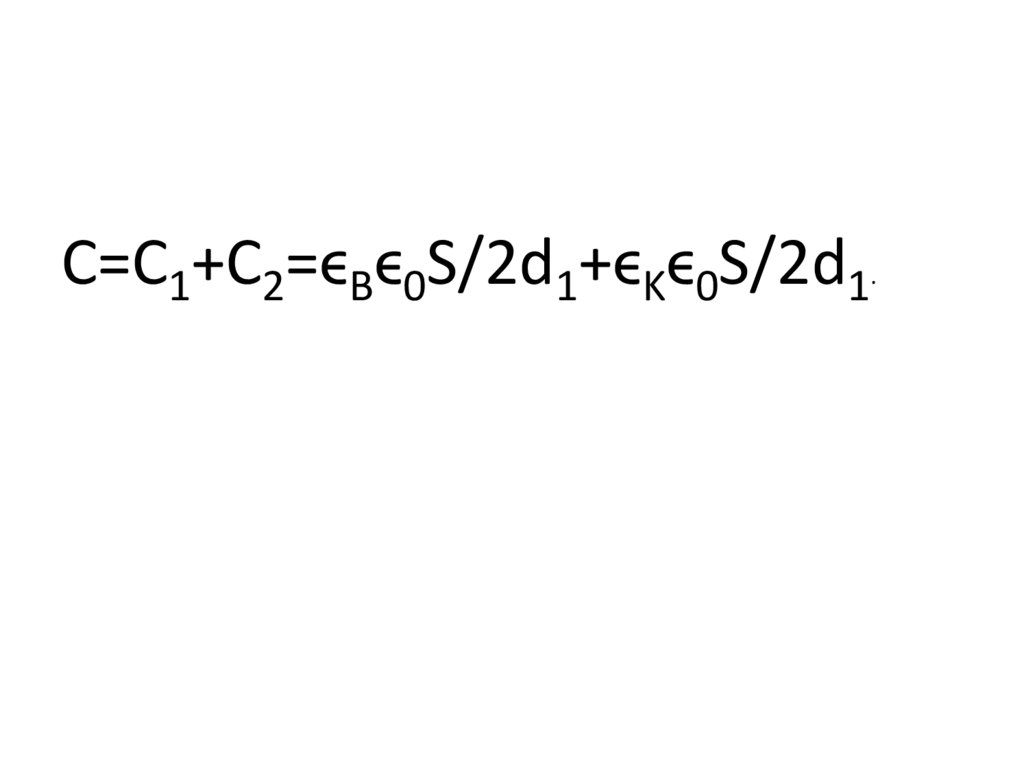






 Физика
Физика








