Определение реакций опор твёрдого тела. Расчётная лабораторная работа № 4

1.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА РФ
ФЕДКРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МОРСКОЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
им. адм. Г. И. Невельского
Кафедра теоретической механики и сопротивления материалов
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
ОПОР ТВЁРДОГО ТЕЛА
Расчётная лабораторная работа № 4
(С – 10)
Составил В. Г. Непейвода
Владивосток
2013
1

2.

Содержание
1. Цель лабораторной работы
2. Основные понятия и определения
3. Метод двойного проецирования
4. Момент силы относительно оси
5. Применение теоремы Вариньона
6. План решения задач статики
7. Пример выполнения задания
2

3.

1. Цель лабораторной работы
Отработка навыков составления расчётных схем и уравнений
равновесия для узлов и тел, находящихся в равновесии под
действием пространственной произвольной системы сил.
Для достижения поставленных целей необходимо изучить
материалы следующих тем:
1. Основные понятия и определения статики.
2. Аксиомы статики.
3. Связи. Силы реакции связей.
4. Пространственная произвольная система сил.
3

4.

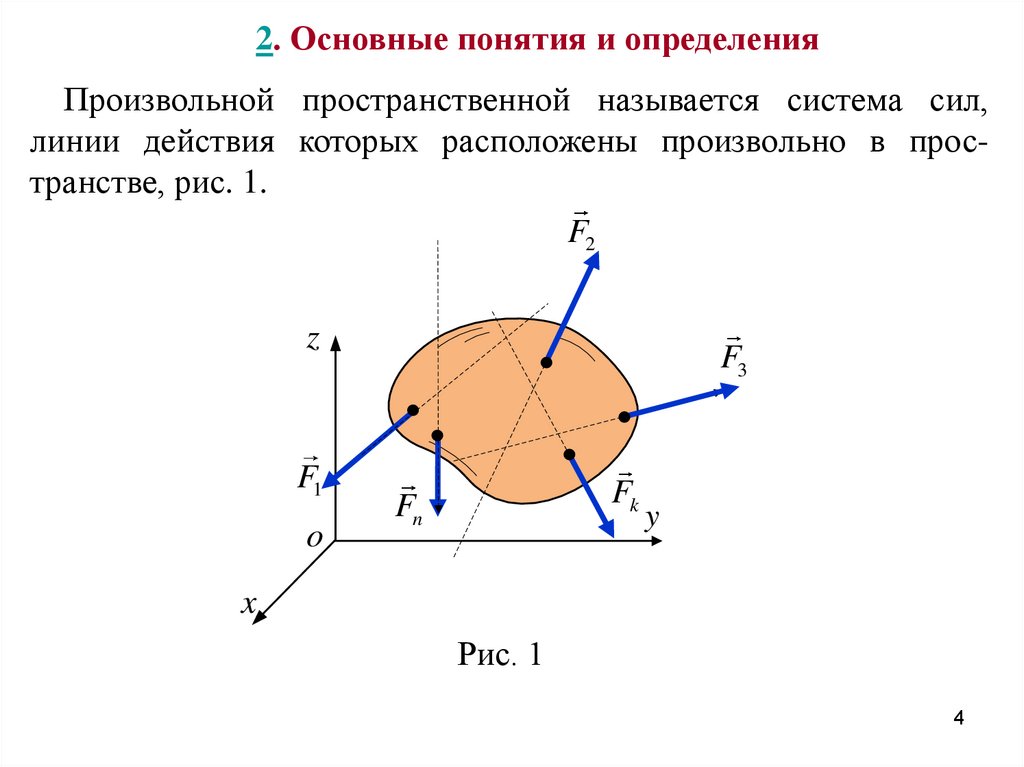
2. Основные понятия и определения
Произвольной пространственной называется система сил,
линии действия которых расположены произвольно в пространстве, рис. 1.
F2
z
F1
o
F3
Fk
Fn
y
x
Рис. 1
4

5.

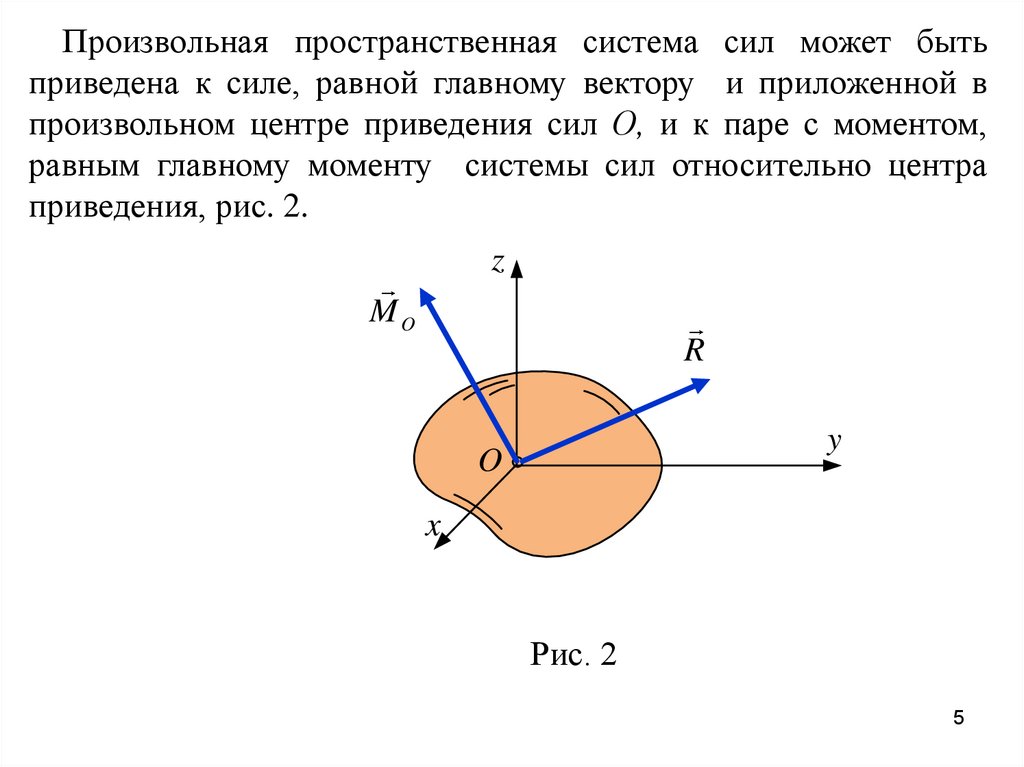
Произвольная пространственная система сил может быть
приведена к силе, равной главному вектору и приложенной в
произвольном центре приведения сил О, и к паре с моментом,
равным главному моменту системы сил относительно центра
приведения, рис. 2.
z
MO
R
y
O
x
Рис. 2
5

6.

При равновесии тела под действием произвольной пространственной системы сил выполняются векторные условия равновесия:
R 0; M O 0.
Из векторных условий равновесия следуют уравнения равновесия:
n
n
n
F
k 1
kx
0;
F
k 1
ky
0;
F
k 1
kz
0;
m F 0; m F 0; m F 0.
n
k 1
n
x
k
k 1
n
y
k
k 1
z
k
Таким образом, для того, чтобы тело под действием
пространственной произвольной системы сил находилось в
равновесии, необходимо и достаточно, чтобы суммы проекций
сил на координатные оси x, y, z и суммы моментов сил относительно этих осей равнялись нулю.
6

7.

3. Метод двойного проецирования силы на ось
Проекции силы, расположенной произвольно в пространстве,
на координатные оси определяется методом двойного проецирования в следующей последовательности, рис. 3:
1) проецируем силу на плоскость, в которой лежит ось;
z
F
F ' F cos ;
y
Fy
O
Fx
b
F'
x
Рис. 3
7

8.

2) полученный вектор проецируем на оси, применив стандартный способ определения проекции силы,
z
F
O
Fy
Fx
b
y
F'
x
Рис. 3
Fx F ' cos b F cos cos b; Fy F ' sin b F cos sin b.
8

9.

Пример 1. Определить проекции силы на координатные оси,
рис. 4.
z
Проекции силы на оси x, y, z
равны:
Fx F cos sin b;
c
Fy F cos cos b;
F
y
b
b
x
Fz F sin .
a
Рис. 4
9

10.

4. Момент силы относительно оси
Момент силы относительно оси характеризует вращательную
способность силы относительно выбранной оси, является
алгебраической величиной и определяется в следующей последовательности.
1. Силу необходимо спроецировать на плоскость, перпендикулярную данной оси, и определить полученную при этом
проекцию.
2. Найти плечо полученной проекции относительно точки
пересечения оси с плоскостью и определить его.
3. Умножить проекцию на плечо и приписать полученному
произведению знак «+», если при взгляде с положительного
направления данной оси вращения видно, что сила вызывает
вращение тела против хода часовой стрелки. В противном случае
моменту силы присваивается знак «–».
10

11.

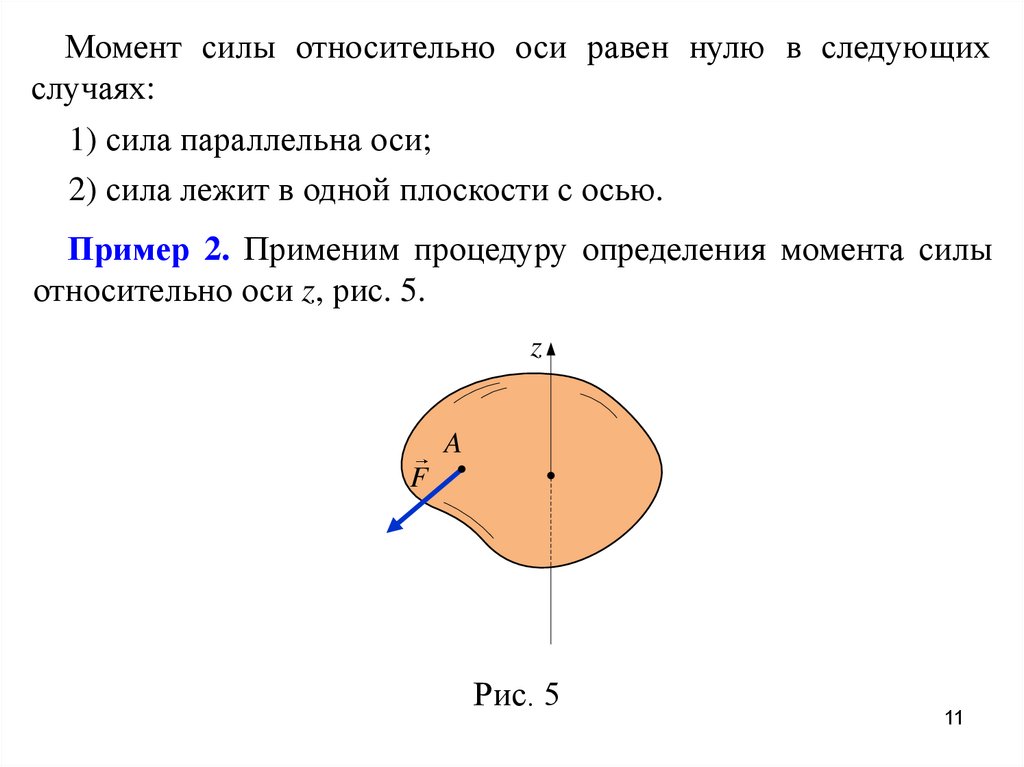
Момент силы относительно оси равен нулю в следующих
случаях:
1) сила параллельна оси;
2) сила лежит в одной плоскости с осью.
Пример 2. Применим процедуру определения момента силы
относительно оси z, рис. 5.
z
A
F
Рис. 5
11

12.

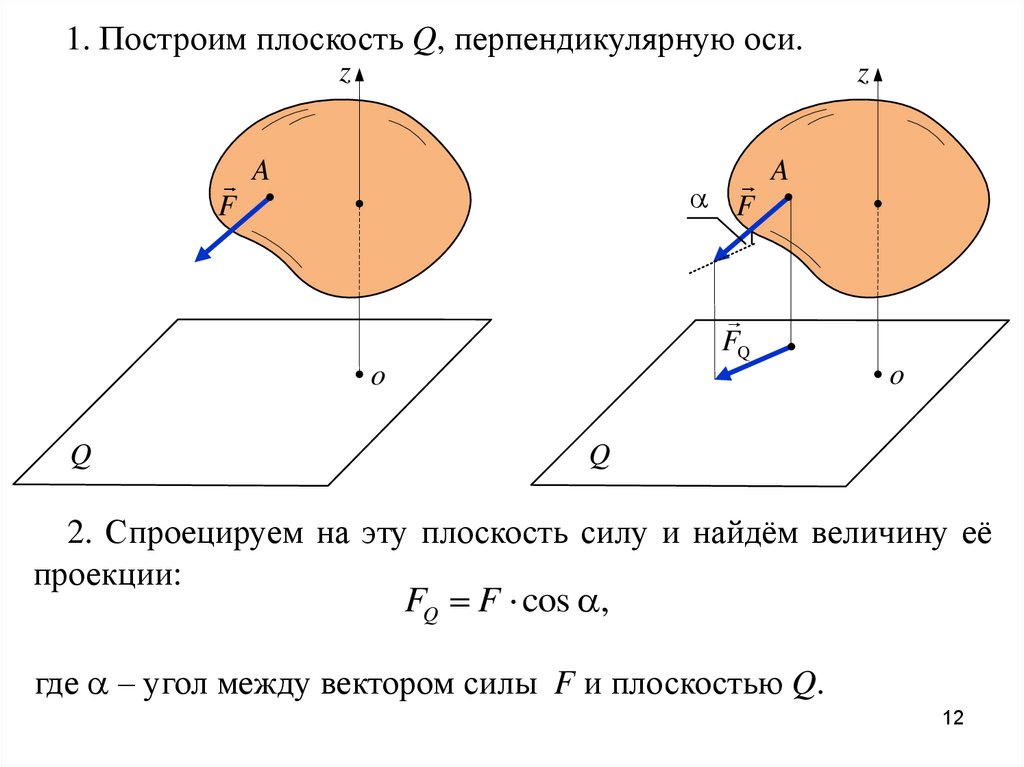
1. Построим плоскость Q, перпендикулярную оси.
z
z
A
F
F
A
FQ
o
o
Q
Q
2. Спроецируем на эту плоскость силу и найдём величину её
проекции:
FQ F cos ,
где – угол между вектором силы F и плоскостью Q.
12

13.

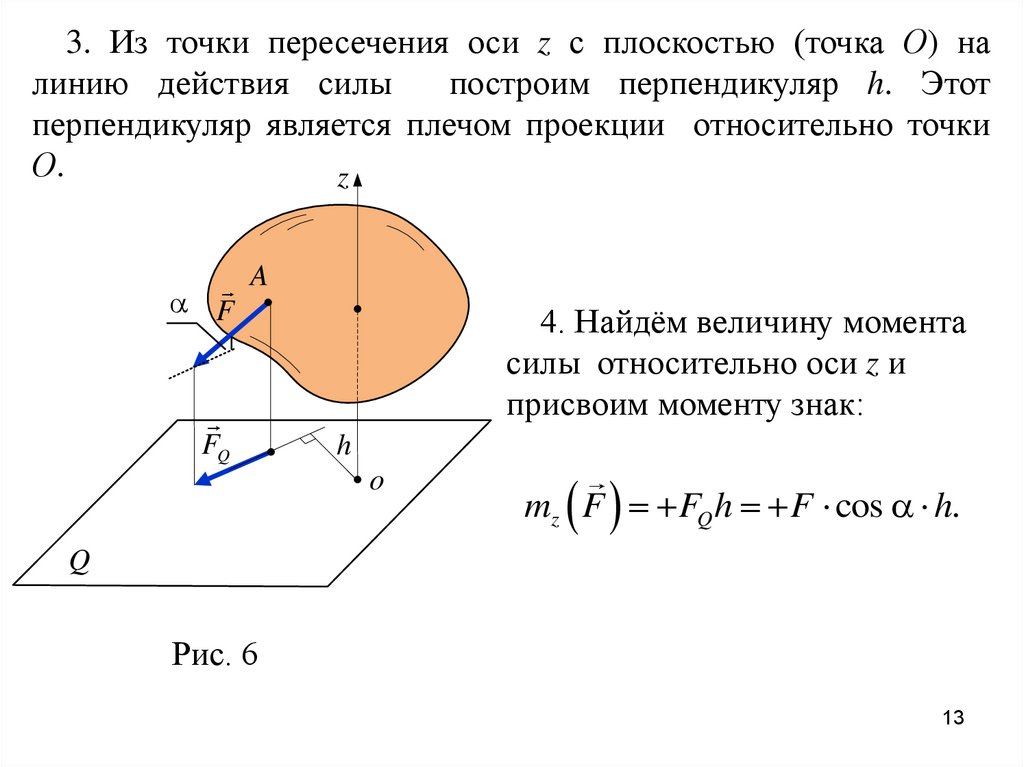
3. Из точки пересечения оси z с плоскостью (точка О) на
линию действия силы
построим перпендикуляр h. Этот
перпендикуляр является плечом проекции относительно точки
О.
z
F
A
FQ
4. Найдём величину момента
силы относительно оси z и
присвоим моменту знак:
h
o
mz F FQ h F cos h.
Q
Рис. 6
13

14.

5. Применение теоремы Вариньона
Если известны углы наклона силы к плоскостям координатных осей, то для вычисления момента силы относительно осей
рекомендуется применять теорему Вариньона.
Применительно к оси теорема читается так: момент равнодействующей силы относительно какой-либо оси равен алгебраической сумме моментов её составляющих относительно той же
оси.
Теорема Вариньона применяется в следующей последовательности.
1. Сила раскладывается на составляющие по координатным
осям. В общем случае таких составляющих будет три: по x, по y
и по z. В частном случае их может быть две.
2. Момент данной силы определяется как алгебраическая
сумма моментов каждой составляющей. Вполне возможно, что
при этом момент какой-либо составляющей окажется равным
нулю.
14

15.

Пример 2. Определить моменты сил относительно осей x, y, z
с применением теоремы Вариньона, рис. 7.
z
z
F1
F1y
F1
c
F1x
F2 y
c
y
y
F2 z
F3
F2
x
b
a
Рис. 7
F3
F2
b
x
b
b
a
Рис. 8
Разложим силы по координатным осям, рис. 8.
F1x F1 cos ; F1 y F1 sin ; F2 y F2 cos b; F2 z F2 sin b;
15

16.

Определим моменты сил, применяя теорему Вариньона.
z
m F F cos c;
m F F cos a;
z
1
1
1
1
F1
mx F1 F1 sin c;
y
F1y
F1x
F2 y
c
y
F2 z
F3
F2
x
b
b
a
Рис. 8
m F F sin b b;
m F F cos b b;
mx F2 F2 cos b c;
y
2
2
z
2
2
m F F b;
m F 0.
mx F3 F3 a;
y
3
z
3
3
16

17.

z
sin
sin b
a
a 2 b2
c
a2 c2
sin
sin b
a 2 b2
c
a c
2
2
F1
;
F1x
F2 y
c
y
;
F2 z
F3
F2
x
a
F1y
;
b
b
a
Рис. 8
;
17

18.

6. План решения задач статики
При решении задач будем придерживаться следующего плана.
1. Выбрать тело (конструкцию, узел конструкции), равновесие
которого необходимо рассмотреть, чтобы найти неизвестные
величины.
2. Показать активные силы, действующие на тело, а также
известные силы реакций связей, если такие есть.
3. Применить метод освобождения от связей и показать
реакции связей, подлежащие определению.
4. Составить уравнения равновесия.
5. Решить систему уравнений способом подстановки или с
использованием стандартных программ, установленных на
персональном компьютере.
18

19.

7. Пример выполнения задания
Условие задания: однородная прямоугольная пластина
размерами АВ = 1,2 м, ВС = 0,9 м, весом Р = 2 кН прикреплена к
стене сферическим шарниром А и цилиндрическим шарниром В
и удерживается в горизонтальном положении нитью СЕ,
составляющей с плоскостью пластины угол = 30о. К точке С
пластины привязана нить, переброшенная через блок К, на
которой закреплён груз Q весом 3 кН; ; в плоскости пластины
действует пара сил с моментом М = 1,5 кНм (рис. 9).
z
E
B y
A
M
K
x
D
C
P
Q
Рис. 9
19

20.

Определить реакции шарниров А, В и натяжение нити СЕ.
Запишем условие в краткой форме.
Дано: АВ = 1,2 м, ВС = 0,9 м, весом Р = 2 кН, = 30о, Q = 3 кН;
М = 1,5 кНм (рис. 9).
Определить: RА, RВ, SСЕ.
z
E
B y
A
M
K
x
D
C
P
Рис. 9
Q
20

21.

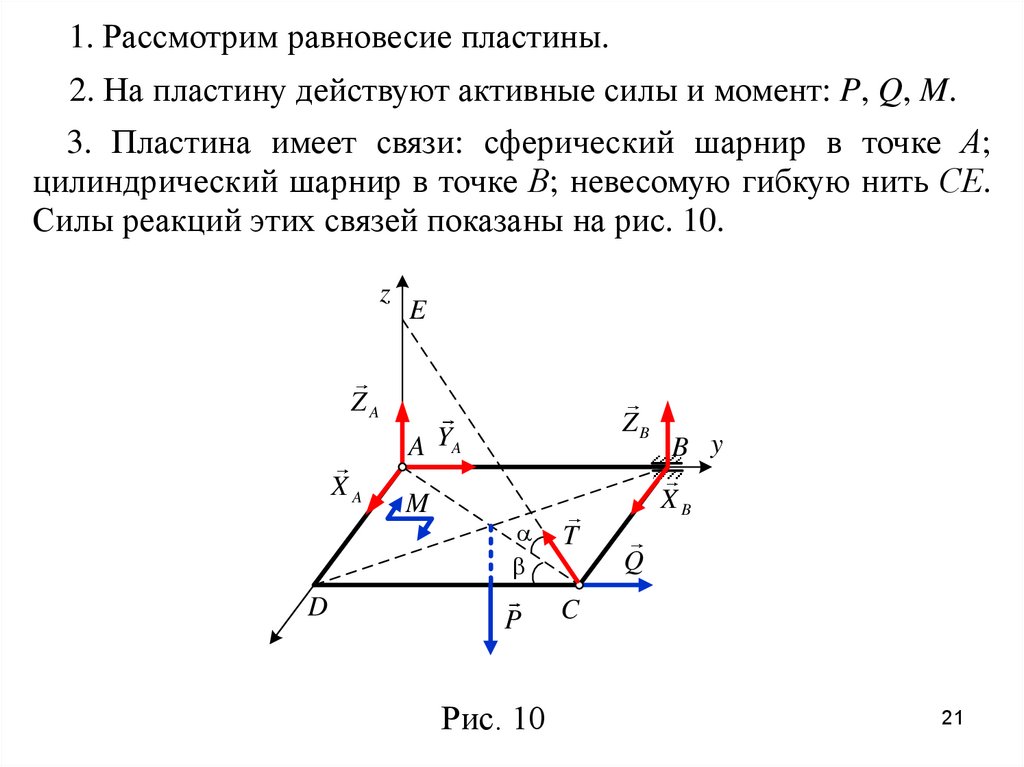
1. Рассмотрим равновесие пластины.
2. На пластину действуют активные силы и момент: P, Q, M.
3. Пластина имеет связи: сферический шарнир в точке А;
цилиндрический шарнир в точке В; невесомую гибкую нить СЕ.
Силы реакций этих связей показаны на рис. 10.
z
E
ZA
ZB
A YA
XA
D
M
b
P
Рис. 10
B y
XB
T
Q
C
21

22.

4. Пластина находится в равновесии под действием пространственной произвольной системы сил. Поэтому составим для
неё 6 уравнений равновесия. Предварительно найдём проекции
силы T на координатные оси методом двойного проецирования.
z
Txy T cos ;
Tx Txy sin b T cos sin b;
Ty Txy cos b T cos cos b.
ZA
kx
A
ky
kz
B
A
A
B
x
ZB
A YA
XA
F 0; X X T 0;
D
F 0; Q Y T 0;
F 0; Z Z T sin P 0;
E
M
b
P
B y
XB
T
Q
C
y
Рис. 10
22

23.

z
E
ZA
ZB
A YA
XA
D
m F 0;
m F 0;
m F 0;
x
k
y
k
z
k
M
b
P
B y
XB
T
Q
C
Рис. 10
Z B AB T sin AB P 0,5 AB 0;
P 0,5 BC T sin BC 0;
Q BC X B AB M 0.
23

24.

Решаем полученную систему уравнений способом
подстановки.
Из уравнения моментов относительно оси y найдём:
P 0,5 BC T sin BC 0;
0,5 P 0,5 2
T
2 кН ;
sin
0,5
Из уравнения моментов относительно оси x:
Z B AB T sin AB P 0,5 AB 0;
Z B 0,5 P T sin 0,5 2 2 0,5 0;
Из уравнения моментов относительно оси z:
Q BC X B AB M 0.
Q BC M 3 0,9 1,5
XB
1,00 кН ;
AB
1,2
24

25.

Из уравнения проекций сил на ось x:
X A X B Tx 0;
X A X B Tx X B T cos sin b 1 2 0,866 0,6 0,04 кН ;
Из уравнения проекций сил на ось y:
Q YA Ty 0;
YA Ty Q T cos cos b Q 2 0,866 0,8 3 1,61(кН);
Из уравнения проекций сил на ось z:
Z A Z B T sin P 0;
Z A P T sin Z B 2 2 0,5 0 1,00 кН .
Сила YA, значение которой получилось отрицательным, имеет
действительное направление, противоположное направлению,
показанному на расчётной схеме.
25

26.

СПАСИБО ЗА ВНИМАНИЕ
ПРИСТУПАЙТЕ К ВЫПОЛНЕНИЮ СВОИХ ЗАДАНИЙ
26