Динамика точки. Законы Галилея – Ньютона

1. ДИНАМИКА ТОЧКИ. ЗАКОНЫ ГАЛИЛЕЯ – НЬЮТОНА

ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДИНАМИКА
ЛЕКЦИЯ 11

2. ДИНАМИКА

это раздел теоретической механики, в котором
устанавливается и изучается связь между
движением материальных тел и
действующими на них силами
I.
Движение тела задано, требуется найти силы, под
действием которых это движение происходит.
II. Действующие на тело силы заданы, требуется
найти закон движения тела.
2
Введение

3. ДИНАМИКА

Динамика
материальной
точки
Динамика
механической
системы
Под материальной точкой подразумевается тело,
размерами и различаем в движениях отдельных точек
которого можно пренебречь.
3
Введение

4. ИСТОРИЯ 1 ЗАКОНА НЬЮТОНА

Аристотель
384 до н. э. — 322 до н. э.
4
Законы Ньютона
Круговое движение - это самое
совершенное движение,
присущее только небесному
миру.
Естественное движение- это
движение тяжёлого тела вниз к
центру Мира, к центру Земли, и
лёгкого вверх.
Все остальные движения на
Земле насильственные и могут
происходить только под
действием внешних сил
«Всё, что находится в движении,
движется благодаря воздействию
другого»
Нет сил – нет движения

5. ИСТОРИЯ 1 ЗАКОНА НЬЮТОНА

Принцип относительности:
«Для предметов, захваченных
равномерным движением, это последнее
как бы не существует и проявляет своё
действие только на вещах, не
принимающих в нём участия»
Галилей
1564 — 1642
5
Законы Ньютона
Все процессы в инерциальных
системах отсчёта протекают одинаково,
независимо от того, неподвижна ли
система или она находится в состоянии
равномерного и прямолинейного
движения

6. ИСТОРИЯ 1 ЗАКОНА НЬЮТОНА

Принцип инерции:
при отсутствии внешних сил тело либо
покоится, либо равномерно движется
Галилей
1564 — 1642
6
Законы Ньютона

7. ИСТОРИЯ 1 ЗАКОНА НЬЮТОНА

Ньютон
1643 — 1727
7
Законы Ньютона

8. ИСТОРИЯ 1 ЗАКОНА НЬЮТОНА

1 ЗАКОН НЬЮТОНА
«Всякое тело продолжает удерживаться в состоянии покоя
или равномерного и прямолинейного движения, пока и
поскольку оно не понуждается приложенными силами
изменить это состояние»
Существуют такие системы отсчёта,
называемые инерциальными, относительно
которых материальные точки, когда на них не действуют
никакие силы, находятся в состоянии покоя
или равномерного прямолинейного
движения
8
Законы Ньютона

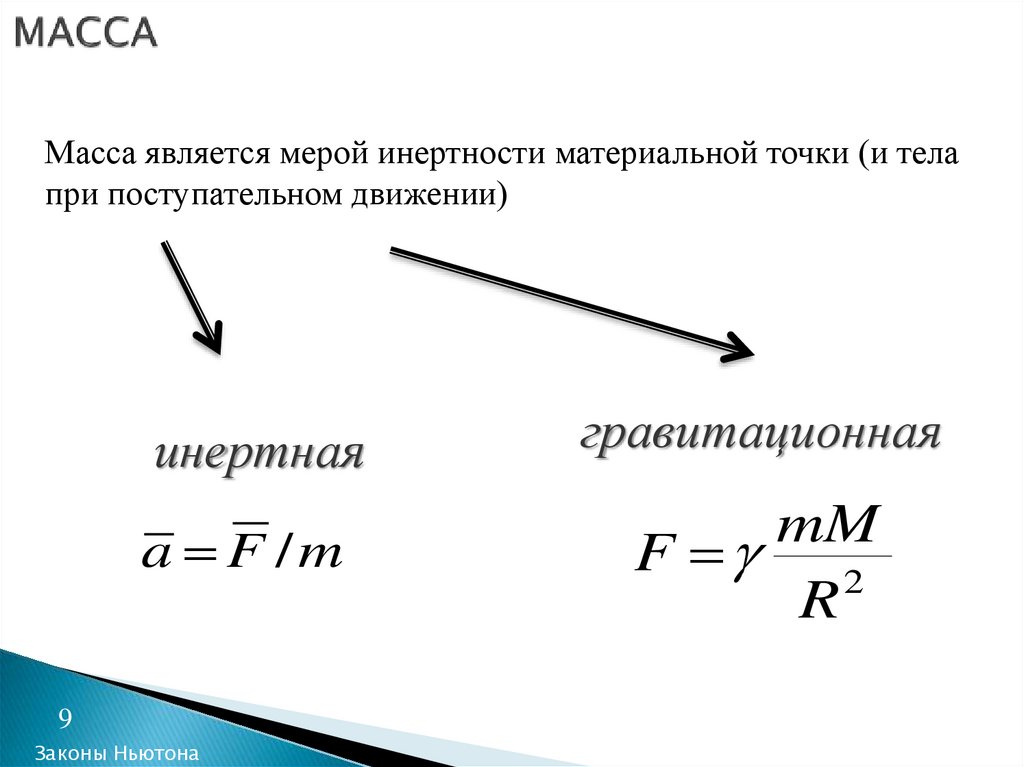
9. МАССА

Масса является мерой инертности материальной точки (и тела
при поступательном движении)
инертная
a F /m
9
Законы Ньютона
гравитационная
mM
F
2
R

10. 2 ЗАКОН НЬЮТОНА

«Изменение количества движения пропорционально
приложенной движущей силе и происходит по направлению той
прямой, по которой эта сила действует»
В инерциальных системах отсчёта ускорение,
приобретаемое материальной точкой, прямо
пропорционально вызывающей его силе, совпадает с ней
по направлению и обратно пропорционально массе
материальной точки
a F /m
ma F
n
10
Законы Ньютона
ma Fk F
k 1

11. 2 ЗАКОН НЬЮТОНА В ДЕКАРТОВОЙ СИСТЕМЕ ОТСЧЕТА

n
ma Fk F
k 1
ma
F
, ma F , ma F
x
x
y
y
z
z
a
x , a
x
y
y , a
z
z
m x F , m y F , m z F
x
y
z
11
2 закон Ньютона

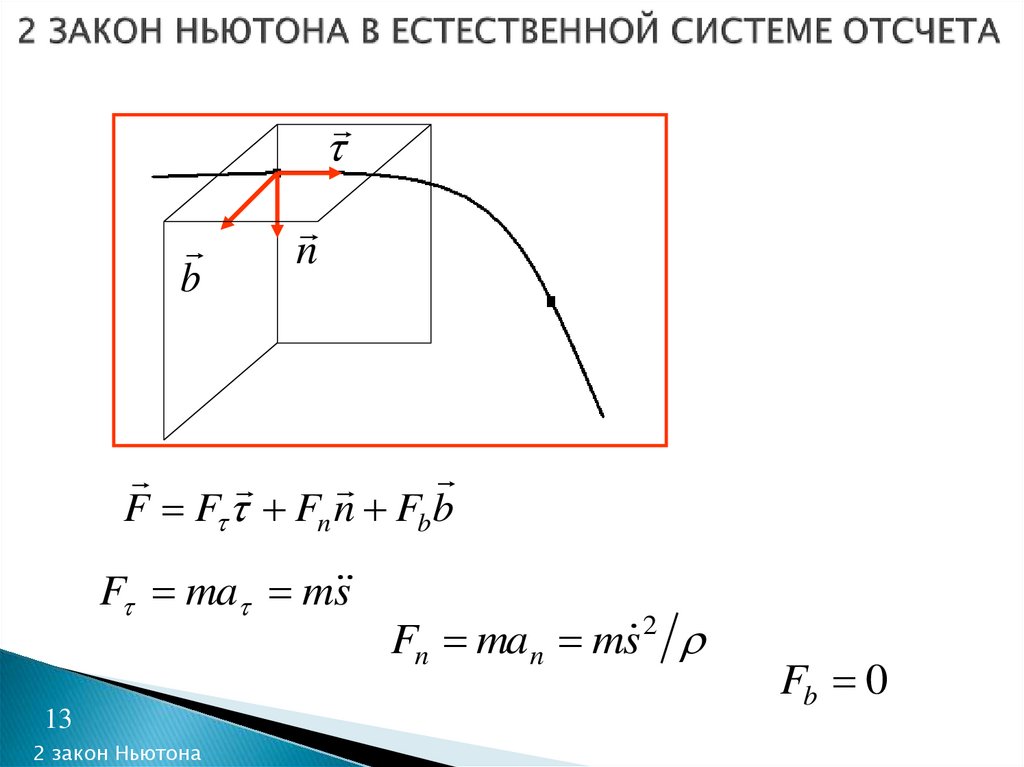
12. 2 ЗАКОН НЬЮТОНА В ЕСТЕСТВЕННОЙ СИСТЕМЕ ОТСЧЕТА

b
n
a a an n abb
a s a s 2
n
12
2 закон Ньютона
ab 0

13. 2 ЗАКОН НЬЮТОНА В ЕСТЕСТВЕННОЙ СИСТЕМЕ ОТСЧЕТА

b
n
F F Fn n Fbb
F ma m s
13
2 закон Ньютона
Fn ma n ms 2
Fb 0

14. СИСТЕМЫ ОТСЧЕТА

Геоцентрическая система отсчета —система отсчета,
связанная с Землей.
Гелиоцентрическая система отсчета —система отсчета,
связанная с Солнцем, причем оси коордитнат
направлены к неподвижным звездам
14
2 закон Ньютона

15. ПРИМЕР РЕШЕНИЯ 1 ЗАДАЧИ ДИНАМИКИ

Точка массой m движется в плоскости х,у по закону х=2sin((π/6)t),
у=2cos((π/6)t). Найти силу, под действием которой происходит это
движение.
x
2
18
sin(
6
y
t ),
2
18
cos(
15
2 закон Ньютона
6
t)
y
m 2
Fx
sin( t ),
18
6
m 2
Fy
cos( t )
18
6
F
M
F
О
x
2
-2
Fx Fy
2
2
m 2
const
18

16. РЕШЕНИЕ 2 ЗАДАЧИ ДИНАМИКИ

m x Fx (t, x, y,z, x , y , z )
m y Fy (t, x, y,z, x , y , z )
x x (t, C1, . ,C6 )
m z Fz (t, x, y,z, x , y , z )
z z (t, C1, . ,C6 )
y y (t, C1, . ,C6 )
Постоянные С1, …. , С6 находятся из начальных
условий
В качестве начальных условий удобно задать
положение и скорость материальной точки в
начальный момент времени.
16
2 закон Ньютона

17. РЕШЕНИЕ 2 ЗАДАЧИ ДИНАМИКИ

Самолет летит на высоте 400м со скоростью 200 м/с. Найти
закон движения груза, сброшенного с самолета.
Сопротивлением воздуха пренебречь.
Рассмотрим движение груза, считая его материальной точкой
y
m x 0,
x 0,
V0
mg
x C1 ,
х
x C1t C3
17
2 закон Ньютона
m y mg
y g
gt C2
y
t2
y g
C2t C4
2

18. РЕШЕНИЕ 2 ЗАДАЧИ ДИНАМИКИ

При t = 0
x 0,
y 400
x 200,
C1 200
C2 0
y 0
C3 0
Закон движения груза:
x 200 t
2
t
y g
400
2
18
2 закон Ньютона
C4 400

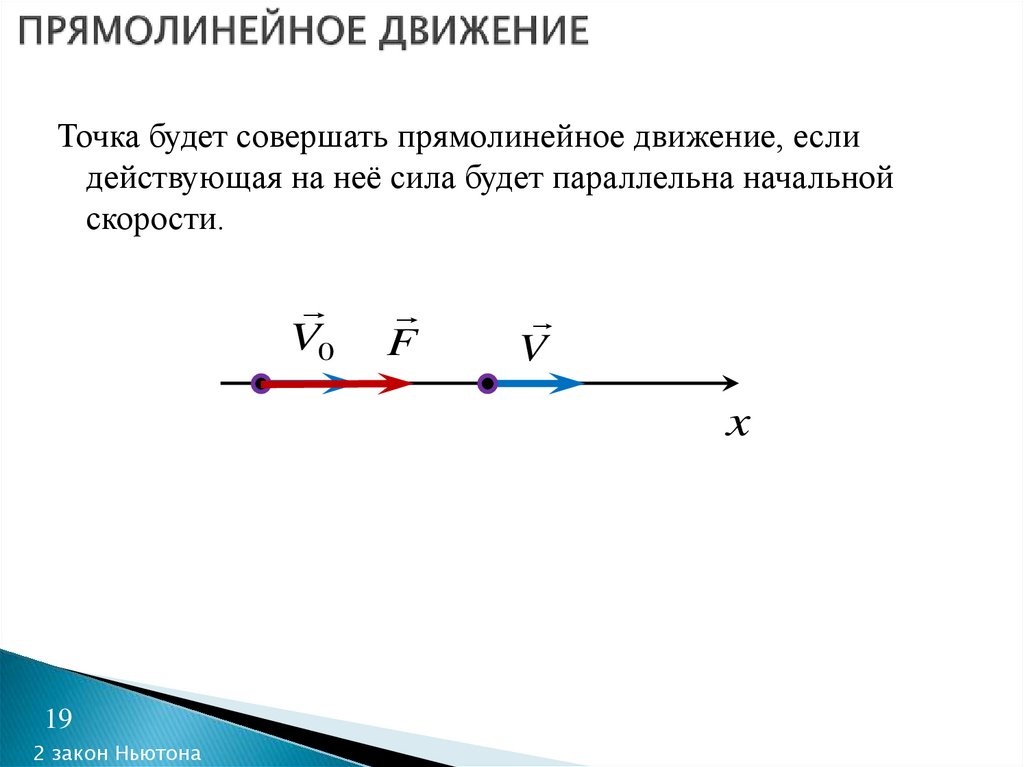
19. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ

Точка будет совершать прямолинейное движение, если
действующая на неё сила будет параллельна начальной
скорости.
V0
F
V
x
19
2 закон Ньютона

20. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ

1. Сила зависит от времени
m x F (t )
x
F F (t )
dx 1
F (t )
dt m x
1
x F (t )dt C
1
m x
1
x F (t )dt dt C t C
1
2
m x
20
2 закон Ньютона

21. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ

F F (V )
2. Сила зависит от скорости
m x F (V )
x
dV
x
dt
dV
m
Fx (V )
dt
dV
t m
C ,
1
F (V )
x
21
2 закон Ньютона
dV
dt m
Fx (V )
t (V ,C )
1

22. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ

3. Сила зависит от координаты
m x F (x)
x
F F (x)
dV
dV
dx
dV
x
V
dt dx dt
dx
1
VdV Fx ( x)dx
m
V
2
2
m
F
V
22
2 закон Ньютона
x
( x ) dx C1
2
Fx ( x)dx C1
m

23. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ

3. Сила зависит от координаты
dx
2
Fx dx C1 ,
dt
m
t
23
2 закон Ньютона
dx
2
Fx dx C1
m
dt
C2
F F (x)
dx
2
Fx dx C1
m

24. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1.Что такое инерциальные системы отсчета?
2. Являются ли инерциальными геоцентрическая и гелиоцентрическая системы
отсчета?
3. Сформулируйте аксиомы динамики (1 и 2 законы Ньютона).
4. Что является мерой инертности материальной точки?
5. Сформулируйте две задачи динамики?
6. Сумма проекций сил на одну из осей естественной системы координат всегда
равна нулю. Что это за ось?
7. Как решать основную задачу динамики, если сила зависит от координаты или
скорости?
24
НА СЛЕДУЮЩЕЙ ЛЕКЦИИ
КОЛЕБАНИЯ ТОЧКИ