Похожие презентации:
Решение показательных неравенств
1. Решение показательных неравенств
Разработалаучитель математики
средней школы № 8
города Елабуги
Герасимова Л.Н.
2. Структура изучения
x2
1
1. Решение неравенства
2. Простейшие показательные
неравенства
3. Решение простейших показательных
неравенств
4. Что нужно учесть при решении
показательных неравенств?
5. Решение неравенств
3.
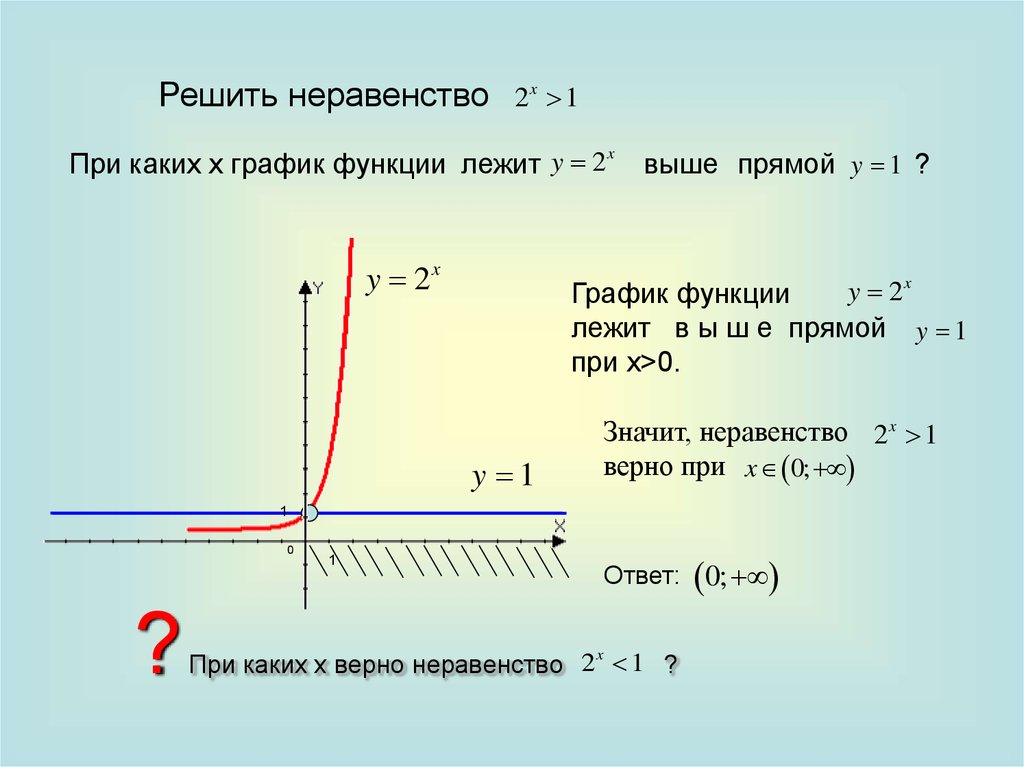
Решить неравенство 2x 1x
При каких х график функции лежит y 2
y 2x
выше прямой y 1 ?
y 2x
График функции
лежит в ы ш е прямой y 1
при x>0.
y 1
Значит, неравенство 2x 1
верно при x 0;
1
0
?
1
Ответ: 0;
x
При каких х верно неравенство 2 1 ?
4.
Простейшие показательныенеравенства
Определение:
Неравенство, содержащее неизвестную в
показателе степени, называется
показательным неравенством.
Определение:
Неравенство в и д а
a f ( x ) a g ( x ) , a 0, a 1
называется простейшим показательным неравенством.
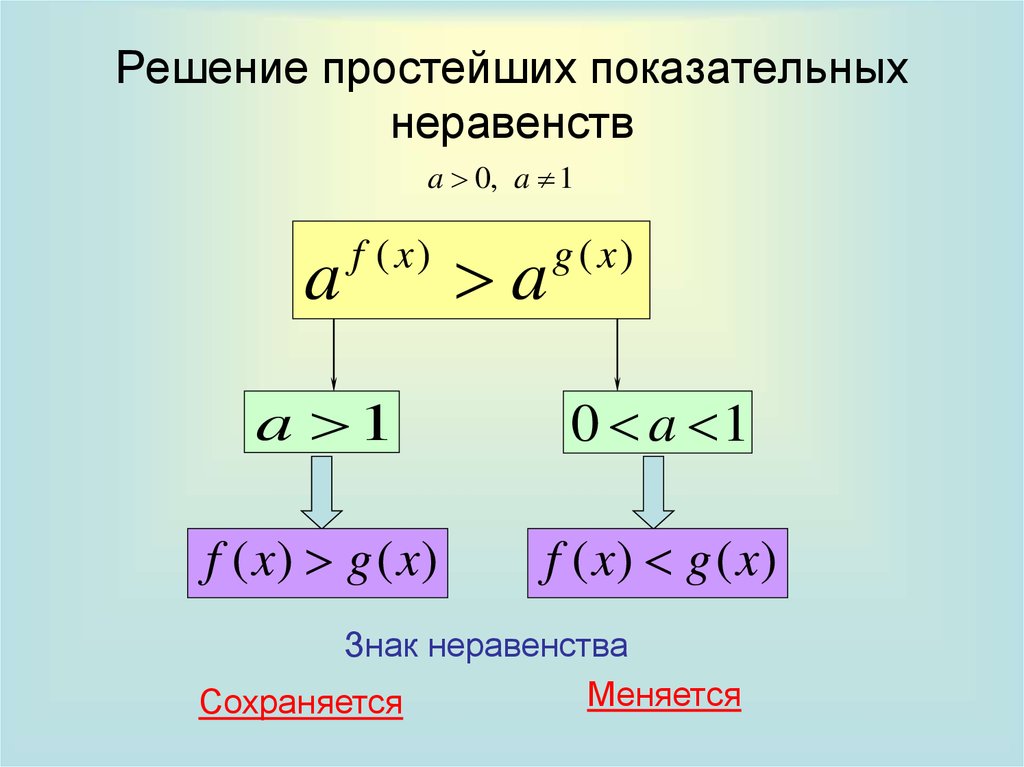
5. Решение простейших показательных неравенств
a 0, a 1a
f ( x)
a
g ( x)
a 1
0 a 1
f ( x) g ( x)
f ( x) g ( x)
Знак неравенства
Меняется
Сохраняется
6. Что нужно учесть при решении показательных неравенств ?
Решить неравенство 2x 12 x 20
x 0.
?
Что нужно учесть при решении простейших
показательных неравенств ?
1. Привести основания степени к одинаковому основанию
2. Использовать свойства монотонной функции
7. Решите неравенства
x8 x 3
8 x 3
3x 81
x R
x
3 x 34
Ответ:
4
2
3 9
x
2
2
2
3 3
x 2
x 4
x
Ответ: Х-любое
x ;4
Ответ:
; 4
4
x
x
2
x 2;
Ответ:
2;
8. Решите неравенство
25x 3
5
2 x 3
1
5
5
3 x 1
1 3 x 1
5 2 x 6 5 3 x 1
2x 6 3<x 1
2x 3x 1 6
x 5
-5
x 5;
x
Ответ:
5;
9. Решите неравенство
1x 5 x
7
7
x 2 5 x
7
7 6
6
2
x 2 5 x 6
x2 5x 6 0
( x 2) ( x 3) 0
+
2 x 3
2
x 2;3
_
2
3
+
3
x
Ответ:
2;3
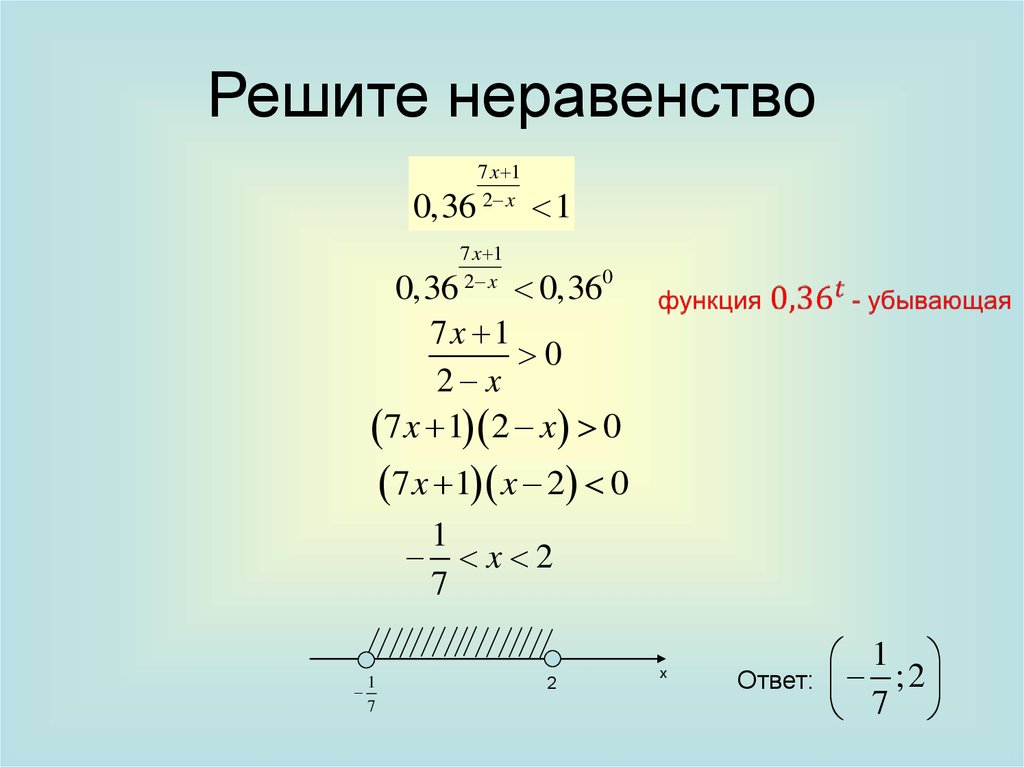
10.
Решите неравенство0,36
7 x 1
2 x
1
7 x 1
2 x
0,36
0,360
7x 1
0
2 x
7 x 1 2 x 0
7 x 1 x 2 0
1
x 2
7
1
7
2
x
Ответ:
1
;2
7









 Математика
Математика








