Динамика вращательного движения. (Тема 4)

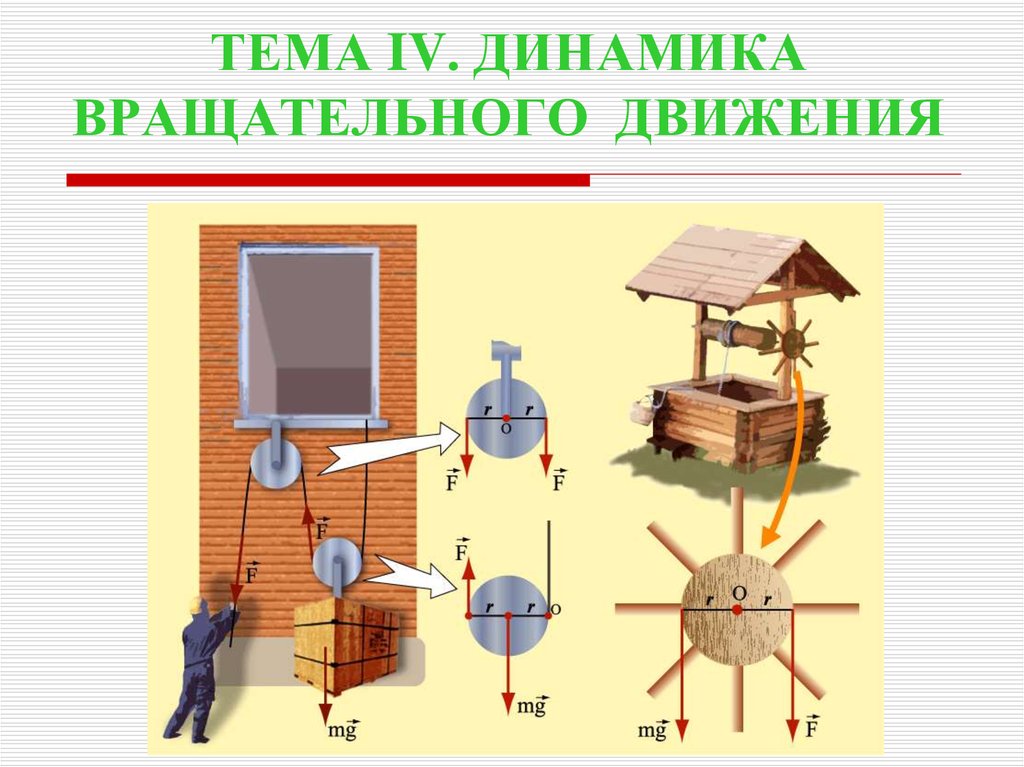
1. ТЕМА IV. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

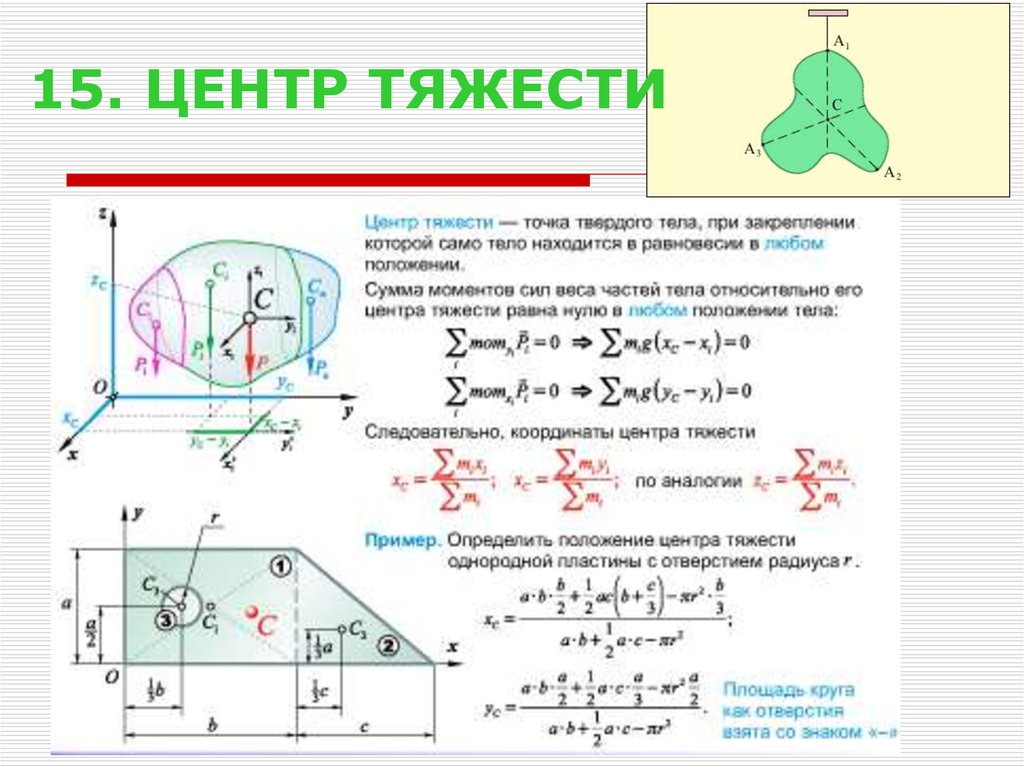
2. 1. ДВИЖЕНИЕ ЦЕНТРА МАСС ТВЕРДОГО ТЕЛА

Центр масс твердого тела движется так, как двигалась бы
материальная точка с массой, равной массе тела,
под действием всех приложенных к телу (внешних) сил.
N
N
N
i 1
i i
N
i 1
m a F . m r r m
i 1
i i
N
i 1
i
i 1
m r mr
N
i 1
mV
i 1
i i
i i
c
N
N
m a f F . f
mi ai fi Fi ;
N
N
i i
c
N
i 1
i
i
mrc .
mV
i i mVc .
i 1
N
mVc mac Fi .
i 1
i 1
i
i 1
i
0

3. 2. МОМЕНТ ИМПУЛЬСА ЧАСТИЦЫ ОТНОСИТЕЛЬНО ТОЧКИ

Моментом импульса частицы
относительно некоторой точки О
называется векторное произведение
радиус-вектора частицы
относительно точки О
на импульс этой частицы
L r p r mV .
Модуль вектора момента импульса частицы
l r sin
L pr sin pl ,
– плечо импульса относительно
точки О (длина перпендикуляра, опущенного
из точки О на линию направления импульса).

4. 3.МОМЕНТ ИМПУЛЬСА ЧАСТИЦЫ ОТНОСИТЕЛЬНО ОСИ

Проекция вектора
момента импульса частицы
на некоторую ось z называется
моментом импульса частицы
относительно этой оси
Lz r p z .
Момент импульса частицы относительно точки – вектор,
момент импульса частицы относительно оси – скаляр.
Lz L cos rp sin cos .
– угол между r и p, – угол между L и осью z.
2
N
L 1 м 1 кг м с 1кг м с.
Lz ri pi z .
Моментом импульса системы частиц
относительно оси z называется величина
i i

5. 4. СВОЙСТВА МОМЕНТ ИМПУЛЬСА

L r p .
1. Псевдовектор. Направление момента импульса определяется
правилом
2. Аддитивность.
3. Зависит от
выбора точки О.
4. Зависит от
системы отсчёта.

6. 4. СВОЙСТВА МОМЕНТ ИМПУЛЬСА

L r p .
1. Псевдовектор.
2. Аддитивность.
3. Зависит от
выбора точки О.
4. Зависит от
системы отсчёта.

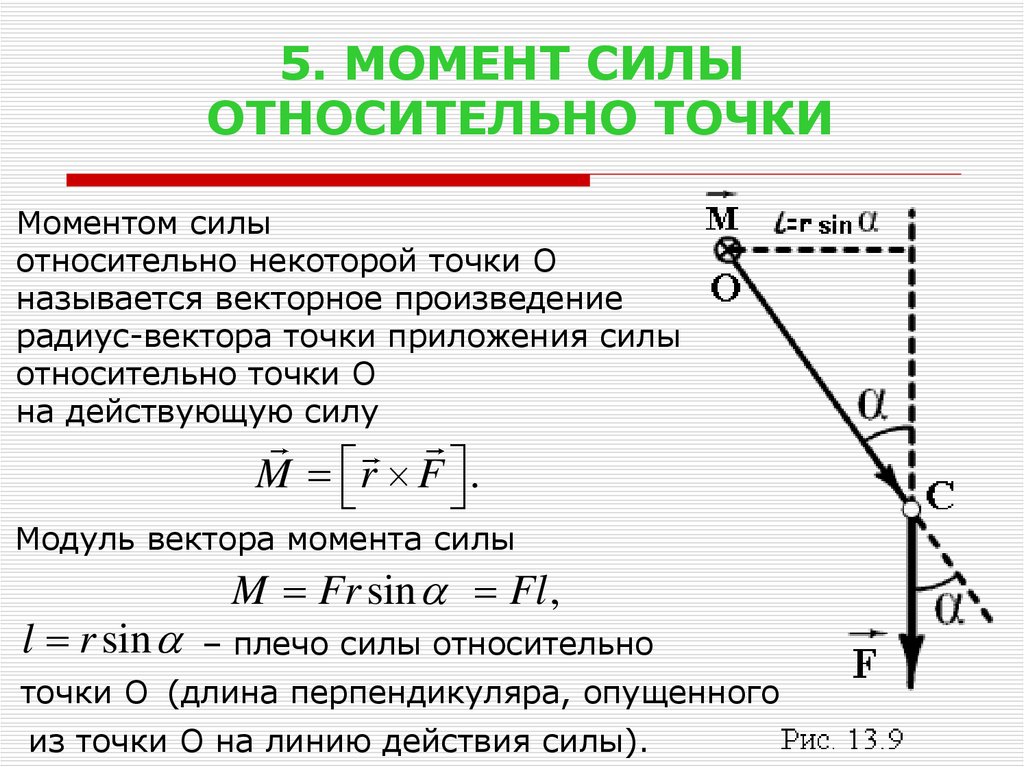
7. 5. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ

Моментом силы
относительно некоторой точки О
называется векторное произведение
радиус-вектора точки приложения силы
относительно точки О
на действующую силу
M r F .
Модуль вектора момента силы
l r sin
M Fr sin Fl ,
– плечо силы относительно
точки О (длина перпендикуляра, опущенного
из точки О на линию действия силы).

8. 6. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ

Проекция вектора
момента силы
на некоторую ось z называется
моментом силы
относительно этой оси
M z r F
z
M z M cos rF sin cos .
– угол между r
– угол между M
M 1 м 1 Н
и
F.
и осью z.
1 Н м.

9. 7. КОМПОНЕНТЫ МОМЕНТА СИЛЫ

M r F
i
rx
Fx
j
ry
Fy
k
rz
Fz
i ( yFz zFy )
j ( zFx xFz )
k ( xFy yFx ).
Вклад в Mz даёт только
компонент силы,
перпендикулярный
плоскости рисунка.

10. 8. УРАВНЕНИЕ МОМЕНТОВ (I)

Запишем уравнение движения для отдельной частицы
и умножим его векторно на радиус-вектор этой частицы
относительно некоторой точки О:
dV
m
F
dt
dV
dV
r m dt r F m r dt M .
Рассмотрим тождество
dV dr
dV
d
r V r
,
V r
dt
dt dt
dt
так как
V V 0.

11. 8. УРАВНЕНИЕ МОМЕНТОВ (II)

dV
d
r V r
Мы доказали, что
,
dt
dt
dV
следовательно уравнение
m r
M
dt
примет вид
d
d
r mV M
m r V M
dt
dt
dL
d
r p M dt M .
dt
Скорость приращения
момента импульса частицы
равна действующему
на частицу моменту сил.

12. 9. УРАВНЕНИЕ МОМЕНТОВ ДЛЯ СИСТЕМЫ ЧАСТИЦ

N
r mV
mV
i i ri f ij ri Fi .
i i f ij Fi ; i
j 1, j i
j 1, j i
N
d
r mV r mV r mV V mV r mV r mV
dt
dLi
dt
N
N
N
d N
M Mi
Li M ij M i .
j 1, j i
dt i 1
i , j 1;i j
i 1
ij
M ij M ji 0
N
i , j 1;i j
M ij 0
N
d N
dL
Li M i
M.
dt i 1
dt
i 1

13. 10. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

dL Mdt;
M 0 dL 0 L const.
Момент импульса замкнутой
(изолированной) системы есть
величина постоянная.
M 0;
Mz 0
L const;
Lz const.

14. 11. МОМЕНТ ИМПУЛЬСА ТВЕРДОГО ТЕЛА

Li ri mV
i i mi ri Vi .
ri Vi Li mi rV
i i ; Vi Ri
Lzi Li cos i mi ri Ri sin i ;
ri sin i Ri Lzi mi R z .
2
i
N
N
N
Lz Lzi mi R z z mi R ; I
i 1
i 1
2
i
i 1
2
i
N
m R
i 1
i
2
i
Lz I z .

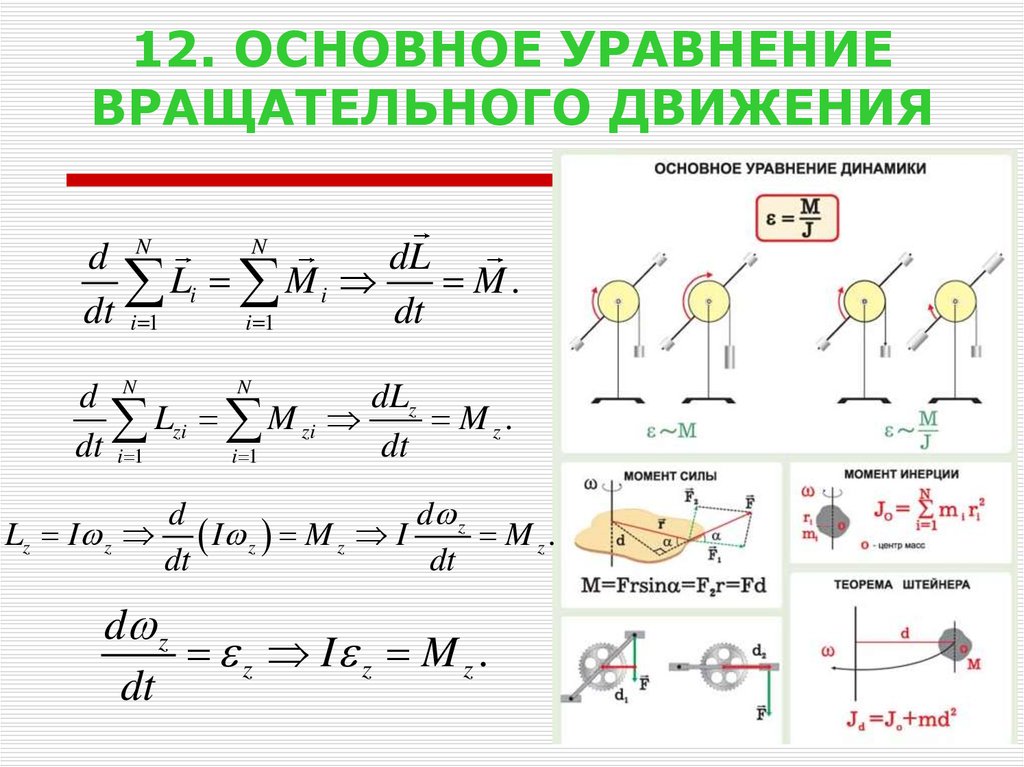
15. 12. ОСНОВНОЕ УРАВНЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

N
d N
dL
Li M i
M.
dt i 1
dt
i 1
N
d N
dLz
Lzi M zi
M z.
dt i 1
dt
i 1
Lz I z
d
d z
I
M
I
M z.
z z
dt
dt
d z
z I z M z .
dt

16. 13. МОМЕНТ ИМПУЛЬСА И МОМЕНТ ИНЕРЦИИ

В общем случае L и не
совпадают по направлению.
Для однородного тела,
симметричного относительно
оси вращения L I .
M 0 L I const.
M z 0 Lz I z const.
I1 z1 I 2 z 2 const;
I1 1 I1 I 2 .

17. 14. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛА

18. 15. ЦЕНТР ТЯЖЕСТИ

19. 16. РЫЧАГИ