Похожие презентации:
Плоская система сил
1.
Тема 6.ПЛОСКАЯ СИСТЕМА СИЛ
Плоской системы сил
называется система сил, как угодно расположенных
в одной плоскости.
6.1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ
ВИДУ.
Плоская система сил приводится к силе, равной R и
приложенной в произвольно выбранном центре О, и паре с
моментом М0, сила и пара лежат в одной плоскости — в
плоскости действия сил.
Значения главного вектора R и главного момента М0 даются
формулами
R Fk , M 0 m0 (Fk )
1
2.
6.1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУВИДУ.
С учётом того, что вектор R для плоской системы сил
можно представить как:
R Rx Ry , и R Rx2 Ry2
Тогда в аналитической форме значения модулей главного
вектора R и главного момента М0 можно записать как:
Rx Fkx
Ry Fky
M 0 m0 (Fk )
Здесь все силы и моменты алгебраические и сумма тоже
алгебраическая.
2
3.
6.1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУВИДУ.
Рассмотрим плоскую систему сил, которая не
находится в равновесии. Приведём её к простейшему виду.
Результат зависит от главного вектора R и главного
момента М0.
1. Если для данной системы сил R = 0, а М0 ≠ 0, то она
приводится к одной паре с моментом М0.. Значение
М0. в этом случае не зависит от выбора центра О.
3
4.
6.1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУВИДУ.
2. Если для данной системы сил R ≠ 0, то она
приводится к одной силе, т. е. к равнодействующей.
При этом возможны два случая:
а) R ≠ 0, Мо = 0.
В этом случае система приводится к равнодействующей R,
проходящей через центр О;
б) R ≠ 0, Мо ≠ 0.
В этом случае пару с моментом Мо можно изобразить двумя
силами R' и R'' ( R' = R, a R'' = -R ).
Из рассмотренных случаев ( 1 и 2) следует, что плоская
система сил, не находящаяся в равновесии, может быть
окончательно приведена или к одной силе, т. е. к
равнодействующей R, когда R ≠ 0 или к паре сил, когда
R = 0.
4
5.
6.2. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙПАРАЛЛЕЛЬНЫХ СИЛ.
Необходимые и достаточные условия равновесия
любой системы сил даются равенствами
R = 0, Мо = 0.
Найдём вытекающие отсюда аналитические условия
равновесия плоской системы сил. Их можно получить в
трёх различных формах.
1. Основная форма условий равновесия.
Для равновесия произвольной плоской системы сил
необходимо и достаточно, чтобы суммы проекций
всех сил на каждую из двух координатных осей и
сумма их моментов относительно любого центра,
лежащего в плоскости действия сил, были равны
5
нулю.
6.
6.2. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙПАРАЛЛЕЛЬНЫХ СИЛ.
1. Первая (основная) форма условий равновесия.
Для равновесия произвольной плоской системы сил
необходимо и достаточно, чтобы суммы проекций
всех сил на каждую из двух координатных осей и
сумма их моментов относительно любого центра,
лежащего в плоскости действия сил, были равны
нулю.
Rx Fkx 0
Ry Fky 0
M 0 m0 (Fk ) 0
Эти равенства выражают условия равновесия твёрдого
тела, находящегося под действием плоской системы сил.
6
7.
6.2. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙПАРАЛЛЕЛЬНЫХ СИЛ.
2. Вторая форма условий равновесия.
Для равновесия произвольной плоской системы сил
необходимо и достаточно, чтобы суммы моментов
всех этих сил относительно каких-нибудь двух
центров А и В и сумма их проекций на ось Ох, не
перпендикулярную прямой АВ, были равны нулю.
Rx Fkx 0
M А mА (Fk ) 0
M В mВ (Fk ) 0
7
8.
6.2. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙПАРАЛЛЕЛЬНЫХ СИЛ.
3. Третья форма условий равновесия.
(уравнения трёх моментов)
Для равновесия произвольной плоской системы сил
необходимо и достаточно, чтобы суммы моментов
всех этих сил относительно любых трёх центров А,
В и С, не лежащих на одной прямой, были равны нулю.
M А m А (Fk ) 0
M В mВ (Fk ) 0
M С mС (Fk ) 0
Во всех рассмотренных случаях для плоской системы сил получаются
три условия равновесия. Первое условие считаются основными, так как
при пользовании ими никаких ограничений на выбор координатных осей
8
и центра моментов не налагается.
9.
6.2. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙПАРАЛЛЕЛЬНЫХ СИЛ.
4. Равновесие плоской системы
параллельных сил
В случае, когда все действующие на тело силы
параллельны друг другу, можно направить ось Ох
перпендикулярно силам, а ось Оу параллельно им .
Тогда проекция каждой из сил на ось Ох будет равна нулю и первое из
уравнений равновесия обратится в тождество вида 0 ≡ 0. В результате
для параллельных сил останется два условия равновесия:
Ry Fky 0
M 0 m0 (Fk ) 0
или
M А mА (Fk ) 0
M В mВ (Fk ) 0
В первом случае ось Оу параллельна силам, во втором - этом точки А и
В не должны лежать на прямой, параллельной силам.
9
10.
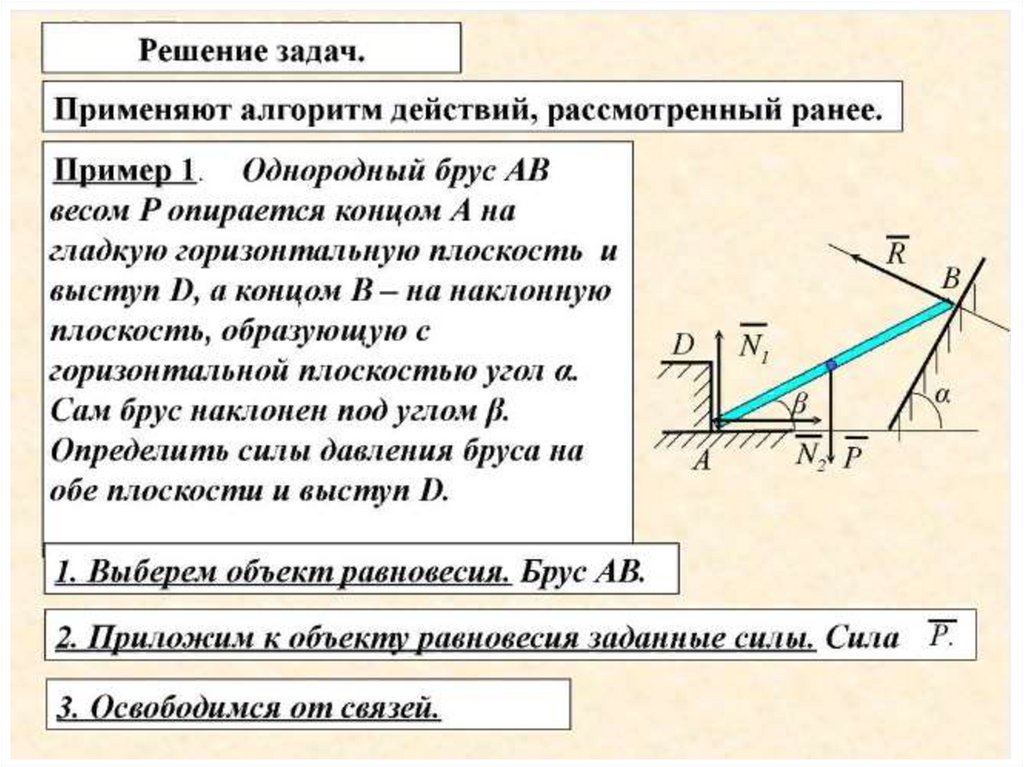
6.3. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙПЛОСКОЙ СИСТЕМЫ СИЛ.
Для получения более простых уравнений
следует (если это только не усложняет ход расчёта):
а) составляя уравнения проекций, проводить координатную
ось перпендикулярно какой-нибудь неизвестной силе;
б) составляя уравнения моментов, брать центр моментов в
точке, где пересекается больше неизвестных сил.
При вычислении моментов иногда бывает удобно разлагать
данную силу на две составляющие и по теореме Вариньона,
находить момент силы как сумму моментов этих
составляющих.
Решение многих задач статики сводится к определению
реакций опор, с помощью которых закрепляются балки,
мостовые фермы и т. л. .
10
11.
6.3. РЕШЕНИЕ ЗАДАЧ НА РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙПЛОСКОЙ СИСТЕМЫ СИЛ.
Чаще всего на практике встречаются задачи, где
фигурируют три основных типа опорных закреплений:
а) подвижная шарнирная опора;
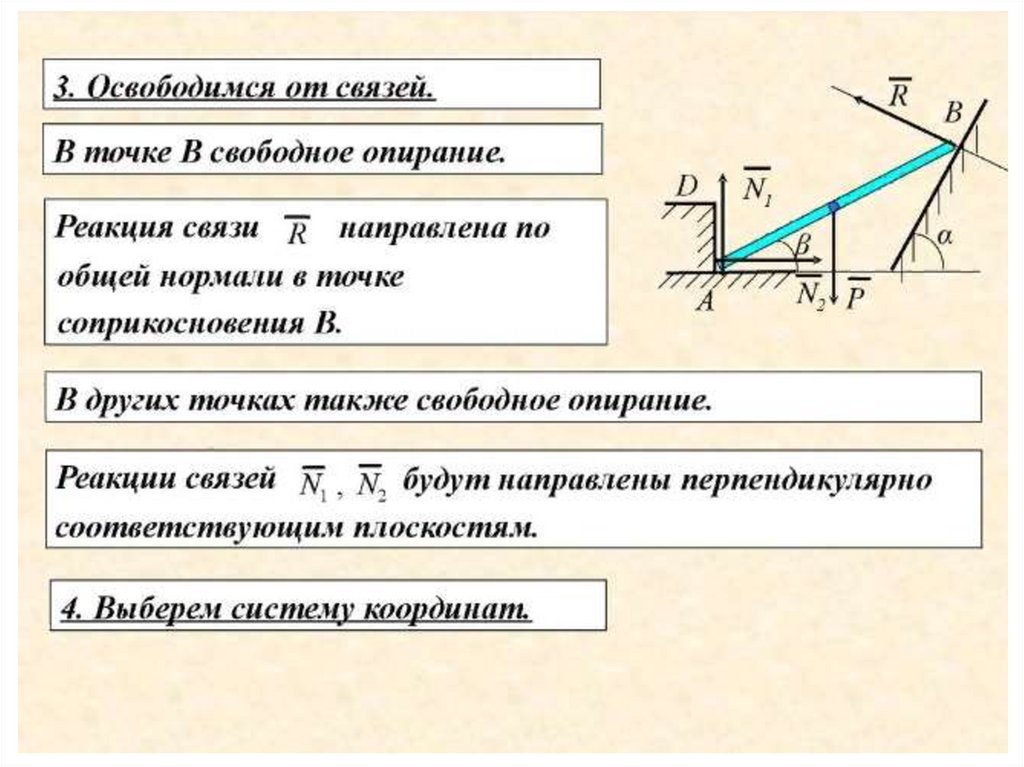
Реакция N такой опоры направлена по нормали к поверхности, на
которую опираются катки подвижной опоры.
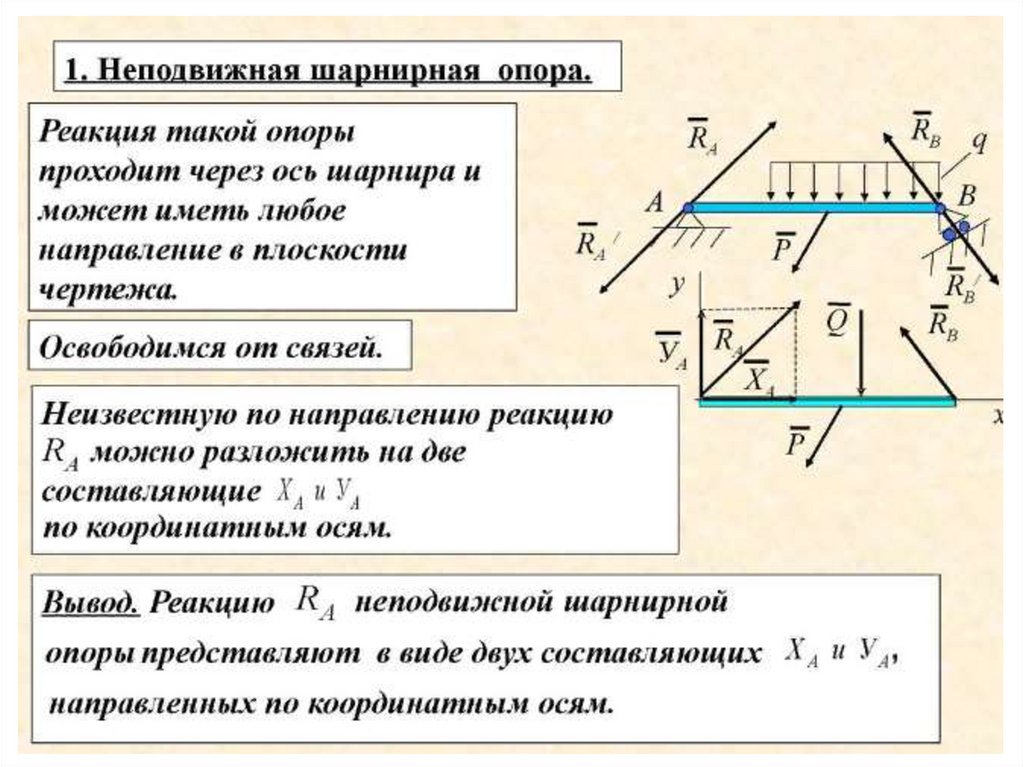
б) неподвижная шарнирная опора;
Реакция R такой опоры проходит через ось шарнира и может иметь
любое направление в плоскости чертежа. При решении задач будем
реакцию R изображать в виде её составляющих Х и Y , направленных
вдоль координатных осей.
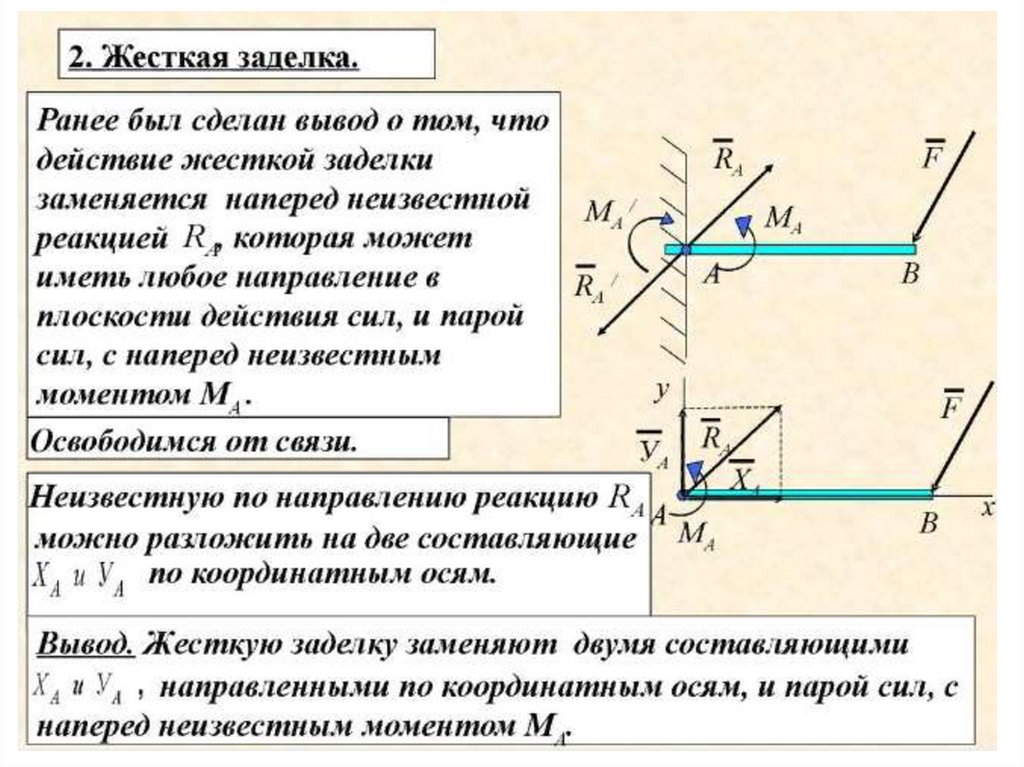
в) жёсткая заделка.
В этом случае на балку в её поперечном сечении действует со стороны
заделанного конца система распределённых сил (реакций). Считая эти
силы приведёнными к центру А сечения, можно их заменить одной
неизвестной силой RA, которая приложена в этом центре, и парой с
неизвестным моментом mА. При решении задач для нахождения реакции
жёсткой заделки надо определить три неизвестные величины ХА, YА, mА.
12.
1213.
14.
1415.
1516.
1617.
1718.
6.3.1. РАВНОВЕСИЕ СИСТЕМЫ ТЕЛ.Решение:
Рассмотрим сначала
равновесие всего
кронштейна. На него
действуют следующие
внешние силы:
- заданные силы Р1, P2, Q
- реакции связей ХА, YA,
ХC, YC
18
19.
Равновесие системы телРешение:
Кронштейн, освобождённый от внешних
связей, не образует жёсткой конструкции
(брусья могут поворачиваться вокруг
шарнира В), но по принципу
отвердевания действующие на него
силы при равновесии должны
удовлетворять условиям равновесия
статики.
Составляя эти условия, найдём:
Fkx X A X C 0
Fky YA YC P1 P2 Q 0
M A ( Fk ) X C 4a YC a P1 2a P2 a Q 4a 0
19
20.
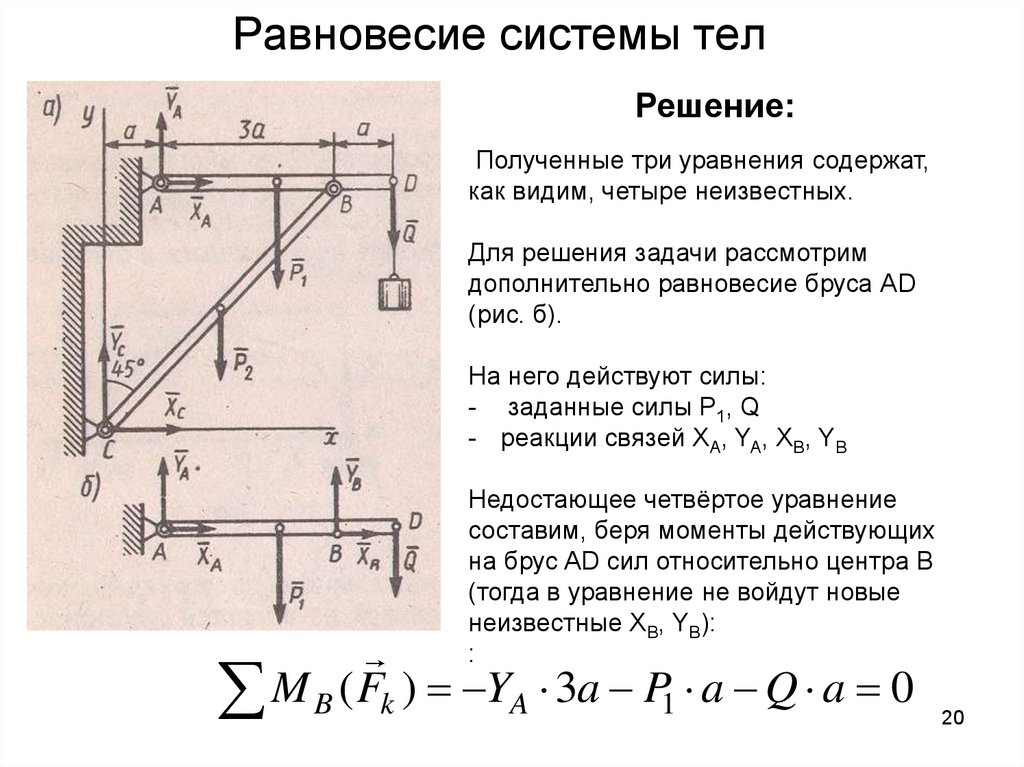
Равновесие системы телРешение:
Полученные три уравнения содержат,
как видим, четыре неизвестных.
Для решения задачи рассмотрим
дополнительно равновесие бруса АD
(рис. б).
На него действуют силы:
- заданные силы Р1, Q
- реакции связей ХА, YA, ХB, YB
Недостающее четвёртое уравнение
составим, беря моменты действующих
на брус AD сил относительно центра В
(тогда в уравнение не войдут новые
неизвестные ХB, YB):
:
M B ( Fk ) YA 3a P1 a Q a 0
20
21.
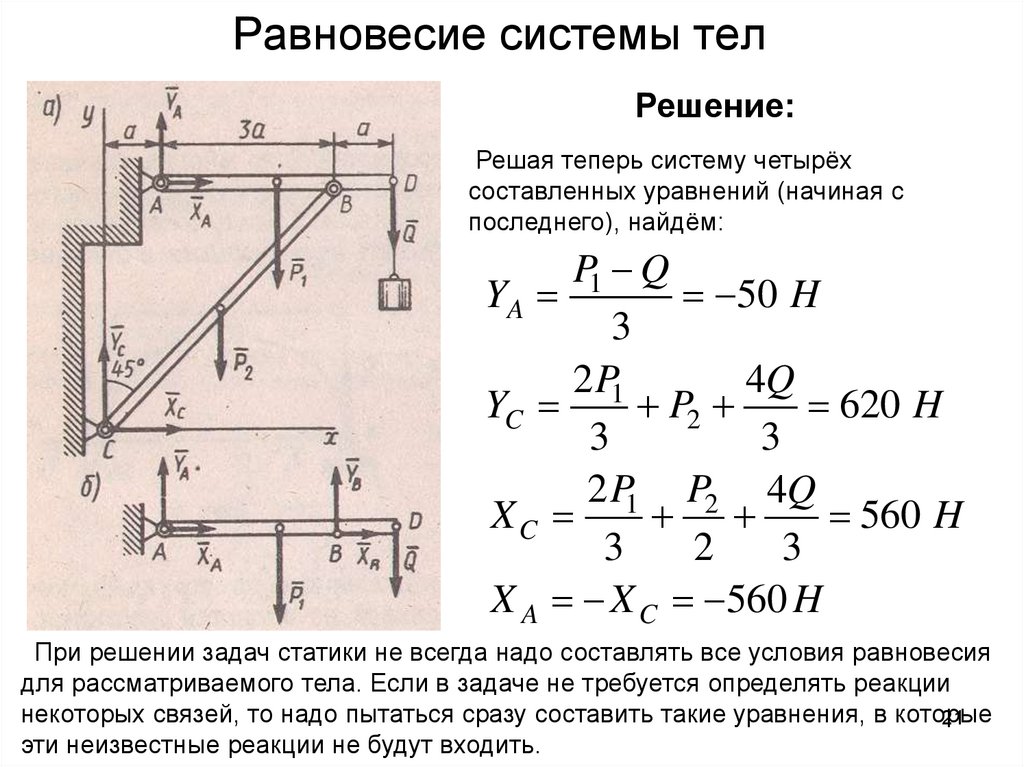
Равновесие системы телРешение:
Решая теперь систему четырёх
составленных уравнений (начиная с
последнего), найдём:
P1 Q
YA
50 H
3
2 P1
4Q
YC
P2
620 H
3
3
2 P1 P2 4Q
XC
560 H
3
2
3
X A X C 560 H
При решении задач статики не всегда надо составлять все условия равновесия
для рассматриваемого тела. Если в задаче не требуется определять реакции
некоторых связей, то надо пытаться сразу составить такие уравнения, в которые
21
эти неизвестные реакции не будут входить.
22.
Равновесие системы телРешение:
Расчленяя систему на
две части,
рассматриваем
равновесие бруса ВК и
балки АВ в
отдельности.
На брус ВК действуют
следующие внешние
силы:
- заданные силы Р
- реакции связей ХВ, YВ,
ND
23.
Равновесие системы телСоставим уравнения равновесия, при
этом, обозначим ВК = а
Fkx X B N D sin 0
Fky YB P N D cos 0
2a Pa
mB ( Fk ) N D 3 2 cos 0
Решая эти уравнения, найдём:
3
N D P cos 212 Н
4
3
X B P sin 2 150 Н
8
3
YB P P cos 2 250 Н
4
23
24.
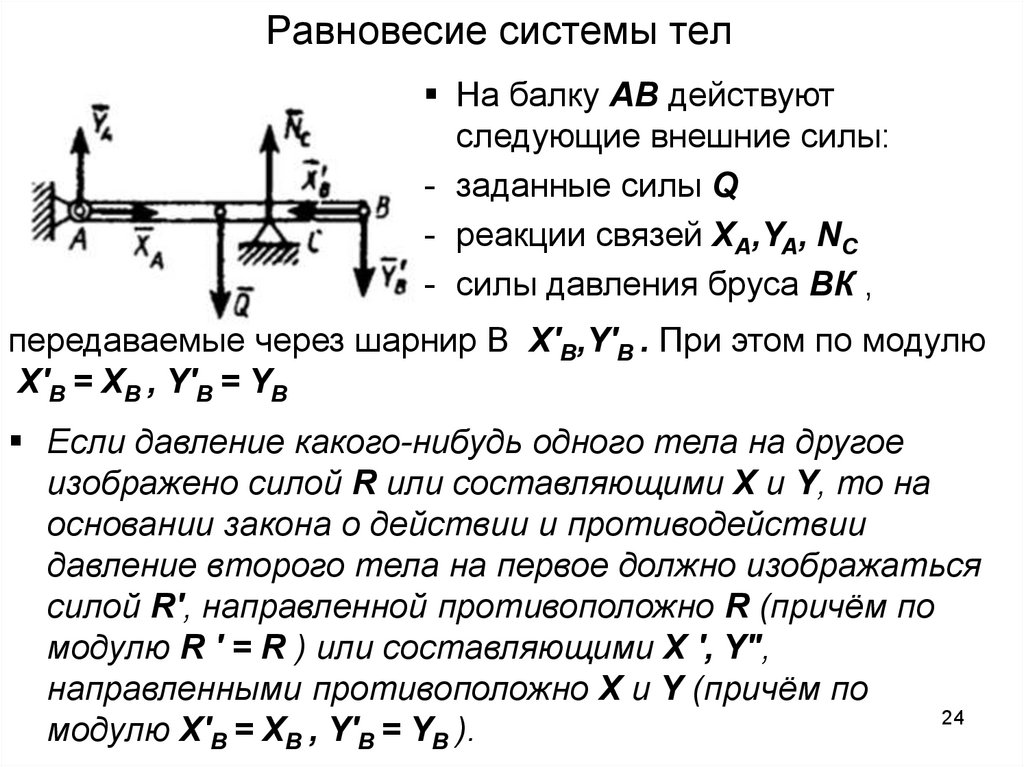
Равновесие системы телНа балку АВ действуют
следующие внешние силы:
- заданные силы Q
- реакции связей ХA,YA, NC
- силы давления бруса ВК ,
передаваемые через шарнир В Х'В,Y'В . При этом по модулю
Х'В = ХВ , Y'В = YВ
Если давление какого-нибудь одного тела на другое
изображено силой R или составляющими X и Y, то на
основании закона о действии и противодействии
давление второго тела на первое должно изображаться
силой R', направленной противоположно R (причём по
модулю R ' = R ) или составляющими X ', Y",
направленными противоположно X и Y (причём по
24
модулю Х'В = ХВ , Y'В = YВ ).
25.
Равновесие системы телСоставим уравнения равновесия,
при этом, обозначим
АВ = b
Fkx X A X B 0
2b
b
mA ( Fk ) YB b NC 3 Q 2 0
2b
b
b
mC ( Fk ) YA 3 Q 6 YB 3 0
Решая эти
уравнения (c учётом
того, что Х'В = ХВ ,
Y'В = YВ, найдём:
X A X B 150 H
Q YB
YA
75 Н
4 4
3Q 3YB
NC
525 Н
4
2
25


















 Физика
Физика








