Статика. Плоская и пространственная системы сил (лекция № 3)

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
Кафедра строительной механики
Теоретическая механика
Тема 1
Статика. Плоская и
пространственная системы сил.
Юлина Анна Олеговна
1

2.

Лекция № 3
Тема 3. Пространственная и плоская системы сил
УЧЕБНЫЕ ВОПРОСЫ
1. Лемма о параллельном переносе сил
2. Главный вектор и главный момент пространственной
системы сил
3. Основная теорема статики (теорема Пуансо)
4. Условия и уравнения равновесия пространственной
системы сил

3.

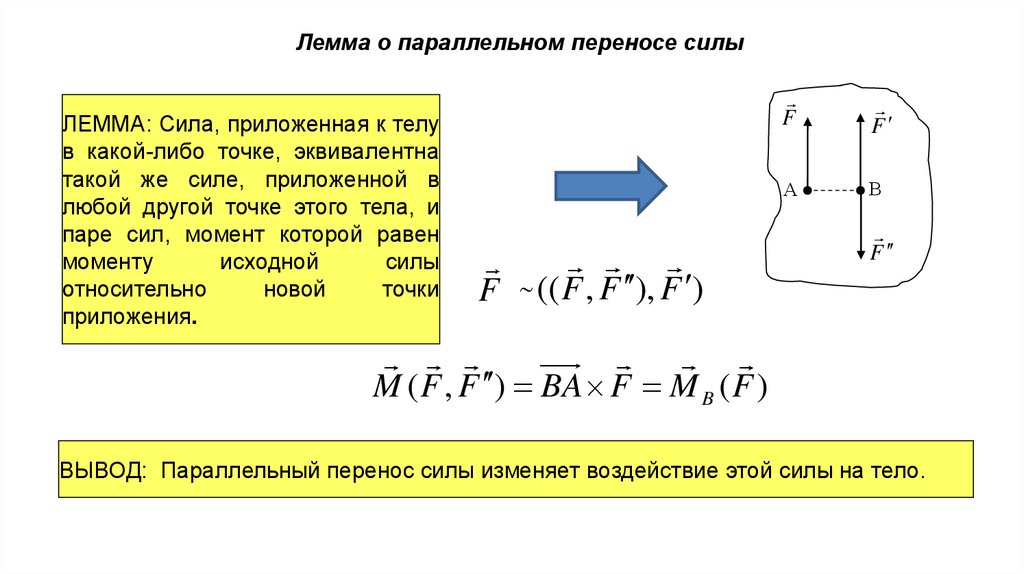
Лемма о параллельном переносе силы
ЛЕММА: Сила, приложенная к телу
в какой-либо точке, эквивалентна
такой же силе, приложенной в
любой другой точке этого тела, и
паре сил, момент которой равен
моменту
исходной
силы
относительно
новой
точки
приложения.
F (( F , F ), F )
F
F
А
В
F
M ( F , F ) BA F M B ( F )
ВЫВОД: Параллельный перенос силы изменяет воздействие этой силы на тело.

4.

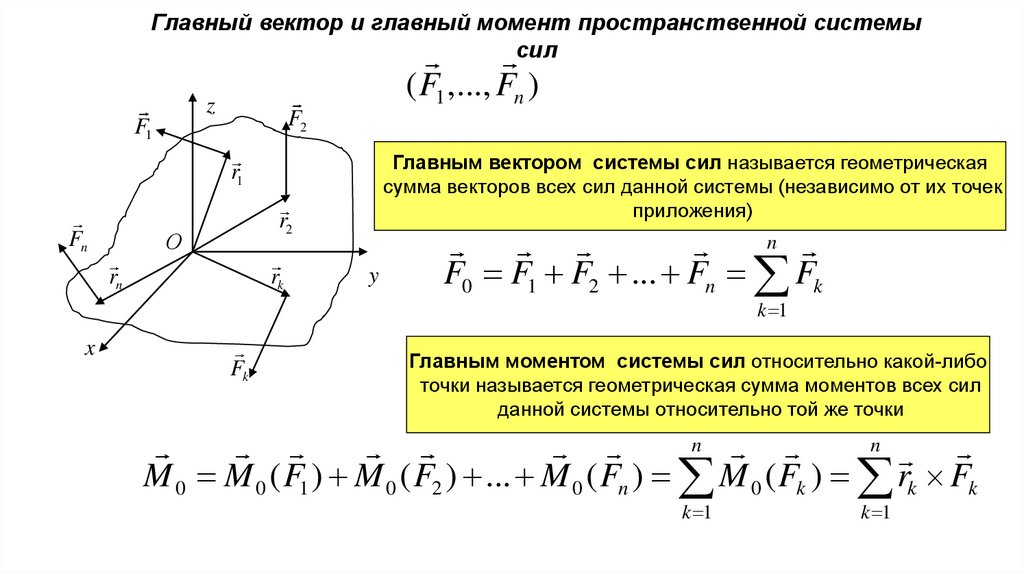
Главный вектор и главный момент пространственной системы
сил
( F1 ,..., Fn )
z
F2
F1
Главным вектором системы сил называется геометрическая
сумма векторов всех сил данной системы (независимо от их точек
приложения)
r1
r2
О
Fn
rn
rk
n
y
F0 F1 F2 ... Fn Fk
k 1
x
Fk
Главным моментом системы сил относительно какой-либо
точки называется геометрическая сумма моментов всех сил
данной системы относительно той же точки
n
n
k 1
k 1
M 0 M 0 ( F1 ) M 0 ( F2 ) ... M 0 ( Fn ) M 0 ( Fk ) rk Fk

5.

Аналитическое вычисление главного вектора и главного момента
Дано: Fk Fkx , Fky , Fkz
T
;
Fox Fkx ;
k 1
n
Foy Fky ;
k 1
n
Foz Fkz .
k 1
n
rk xk , yk , zk
T
M ox ( yk Fkz zk Fky );
k 1
n
M oy ( zk Fkx xk Fkz );
k 1
n
M oz ( xk Fky yk Fkx ).
k 1
F0 Fox2 Foy2 Foz2
Fox cos( j , F ) Foy ; cos(k , F ) Foz
cos(i , F0 )
;
0
0
F0
F0
F0
n
M 0 M ox2 M oy2 M oz2 ;
cos(i , M 0 )
M ox
;.
Mo

6.

Как определить угол между главным вектором и главным
моментом?
Скалярное произведение векторов
Fo M o Fo M o cos( Fo , M o ) Fo x M ox Fo y M oy Fo z M oz
cos( Fo , M o )
Fox M ox Foy M oy Foz M oz
Fo M o
cos(i , Fo ) cos(i , M o ) cos( j , Fo ) cos( j , M o ) cos(k , Fo ) cos(k , M o )

7.

Перемена центра приведения
rk rk O1O
Fk
rk
k
О
n
n
n
k 1
k 1
k 1
M 01 rk Fk (rk Fk ) (010 Fk )
r
O1
n
M o O1O Fk M o O1O Fo
k 1
M 0 M 01 ( F0 )
ВЫВОД: Главный момент при перемене центра приведения изменяется на момент
силы, равной главному вектору, приложенному в старом центре приведения,
относительного нового центра приведения

8.

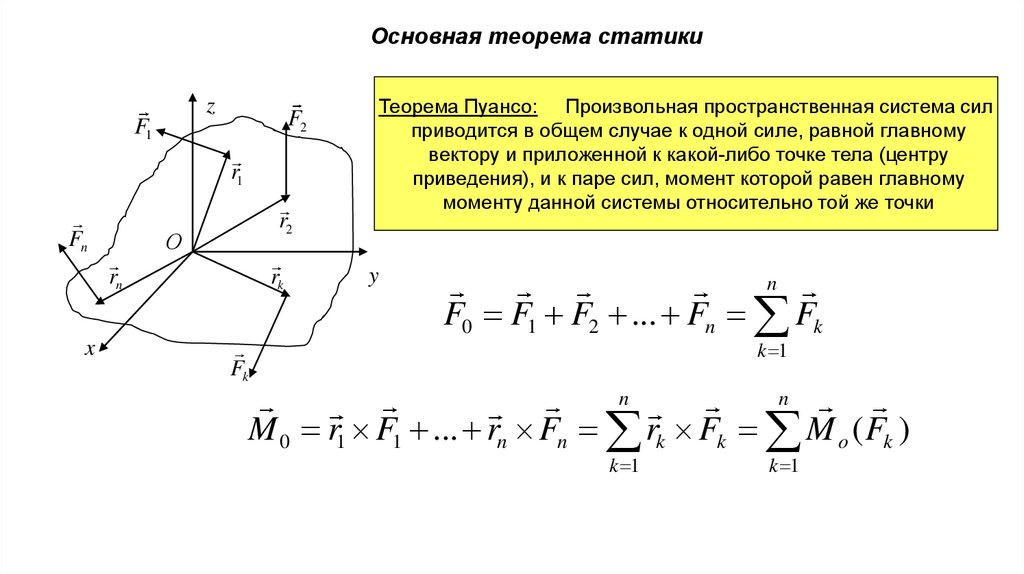
Основная теорема статики
z
Теорема Пуансо: Произвольная пространственная система сил
приводится в общем случае к одной силе, равной главному
вектору и приложенной к какой-либо точке тела (центру
приведения), и к паре сил, момент которой равен главному
моменту данной системы относительно той же точки
F2
F1
r1
r2
О
Fn
rn
x
rk
y
n
F0 F1 F2 ... Fn Fk
k 1
Fk
n
n
k 1
k 1
M 0 r1 F1 ... rn Fn rk Fk M o ( Fk )

9.

Луи Пуансо, 1777 - 1859 г., академик Парижской академии наук

10.

Условия и уравнения равновесия пространственной
системы сил
Теорема:
Для равновесия
произвольной пространственной
системы сил необходимо и
достаточно, чтобы главный
вектор и главный момент этой
системы равнялись нулю.
n
F0 M 0 0
n
n
F 0; F 0; F 0;
k 1
n
kx
k 1
ky
n
k 1
kz
n
M ( F ) 0; M ( F ) 0; M ( F ) 0
k 1
ox
k
k 1
oy
k
k 1
oz
k

11.

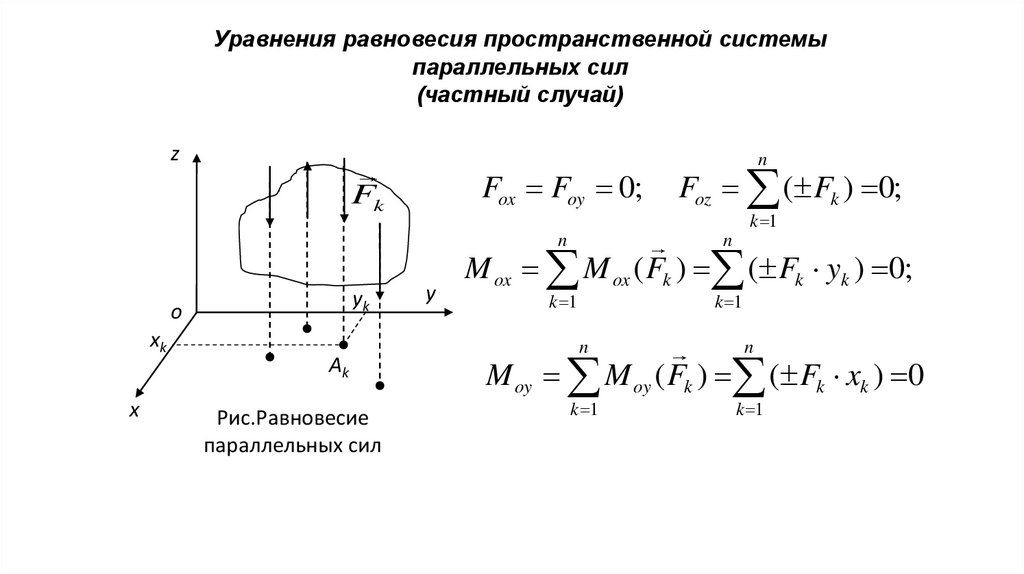
Уравнения равновесия пространственной системы
параллельных сил
(частный случай)
z
Fox Foy 0;
Fk
yk
o
xk
x
Ak
Рис.Равновесие
параллельных сил
y
n
Foz ( Fk ) 0;
k 1
n
n
k 1
k 1
M ox M ox ( Fk ) ( Fk yk ) 0;
n
n
k 1
k 1
M oy M oy ( Fk ) ( Fk xk ) 0