Похожие презентации:
Неопределенный интеграл. Способы нахождения
1. ЕТСТСО
Студентка группы ТПО-1Захарова Мария Юрьевна
2.
Евдокс Книдскийок. 408 — ок. 355 год до н. э.
3.
4.
Готфрид ВильгельмЛейбниц (1646—1716)
Исаак Ньютон
(1643 – 1727)
5.
Работы Коши и Вейерштрассаподвели итог многовековому
развитию интегрального
исчисления.
Огюстен Луи Коши
(1789 – 1857)
Карл Теодор Вильгельм
Вейерштрасс (1815 1897 )
6.
В развитии интегрального исчисленияприняли участие русские математики:
В.Я. Буняковский
(1804 – 1889)
М.В. Остроградский
(1801 – 1862)
П.Л. Чебышев
(1821 – 1894)
7.
Неопределенныминтегралом
от
непрерывной функции f(x) на интервале
(a; b) называют любую ее первообразную
функцию.
f
(
x
)
dx
F
(
x
)
c
Где С – произвольная постоянная (const).
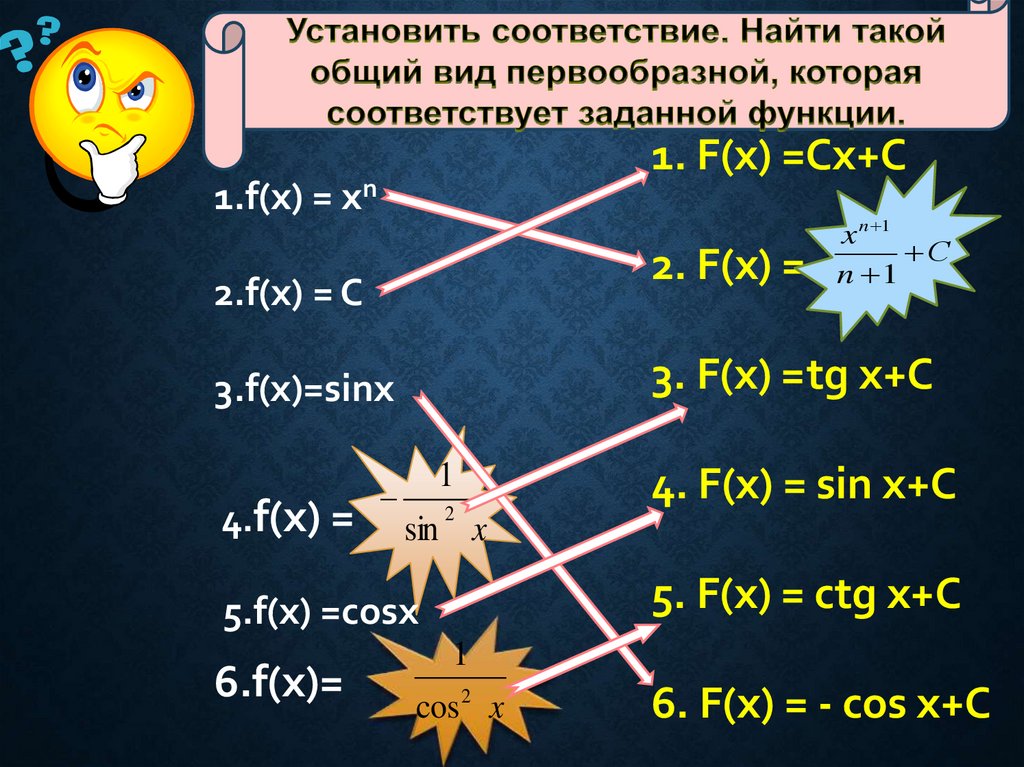
8.
1. F(x) =Сх+С1.f(x) = хn
2. F(x) =
2.f(x) = C
3. F(x) = tg x+С
3.f(x)=sinx
4.f(x) =
1
2
4. F(x) = sin x+С
sin x
5. F(x) = сtg x+С
5.f(x) =cosx
6.f(x)=
x n 1
С
n 1
1
cos 2 x
6. F(x) = - cos x+С
9.
Свойства интеграла(
f
(
x
)
g
(
x
)
)
dx
f ( x)dx g ( x)dx
C
f
(
x
)
dx
Cf
(
x
)
dx
10.
Свойства интегралаf ( х)dx
f ( х)
f ( x)dx f ( x) С
1
f (kx b)dx F (kx b) C
k
11. Основные методы интегрирования
1.Табличный.2.Сведение к табличному
преобразованием подынтегрального
выражения в сумму или разность.
3.Интегрирование с помощью замены
переменной (подстановкой).
4.Интегрирование по частям.
12. Найти первообразные для функций:
1) f(x) =10х2) f(x) =3 х²
3) f(x) =
sinх+5
4) f(x) = 5cosx
5) f(x) = 6х²
6) f(x) = 3-2х
13. Верно ли что:
ВЕРНО ЛИ ЧТО:а)
x
dx
5
x
C
5
в)
3
x
dx
x
C
4
б)
3
x
dx
6
x
C
2
2
г
)
3
1 7
x
dx
x
C
7
6
14.
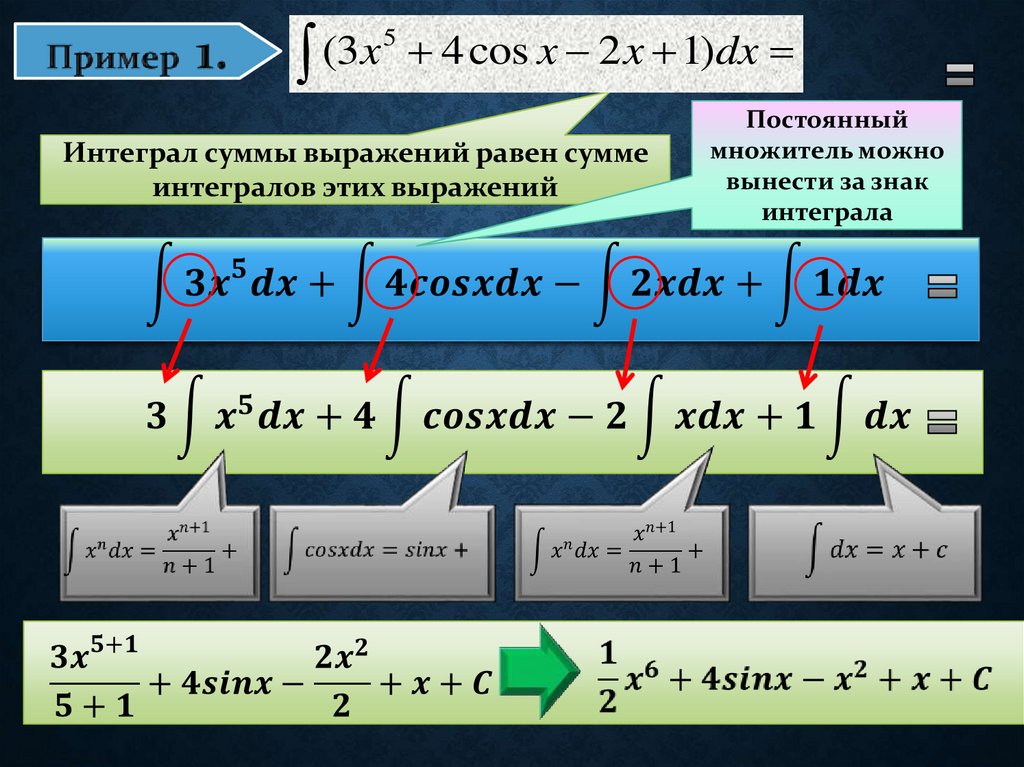
5(
3
x
4 cos x 2 x 1)dx
Интеграл суммы выражений равен сумме
интегралов этих выражений
Постоянный
множитель можно
вынести за знак
интеграла
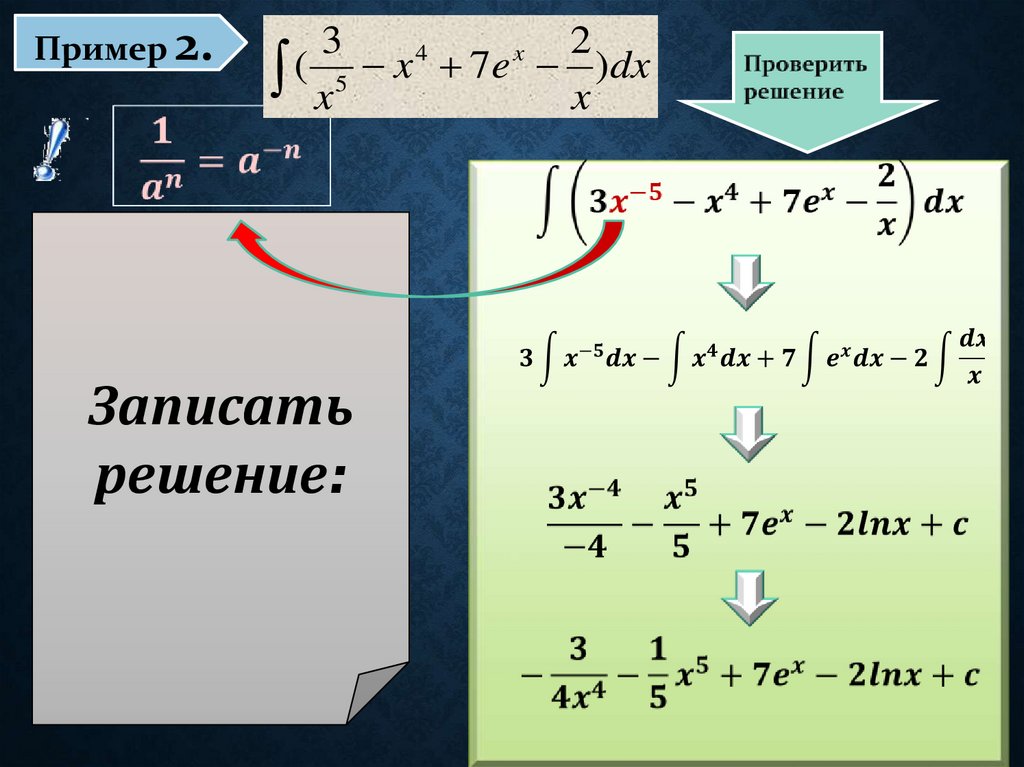
15.
Пример 2.3
2
4
x
( x5 x 7e x )dx
Записать
решение:
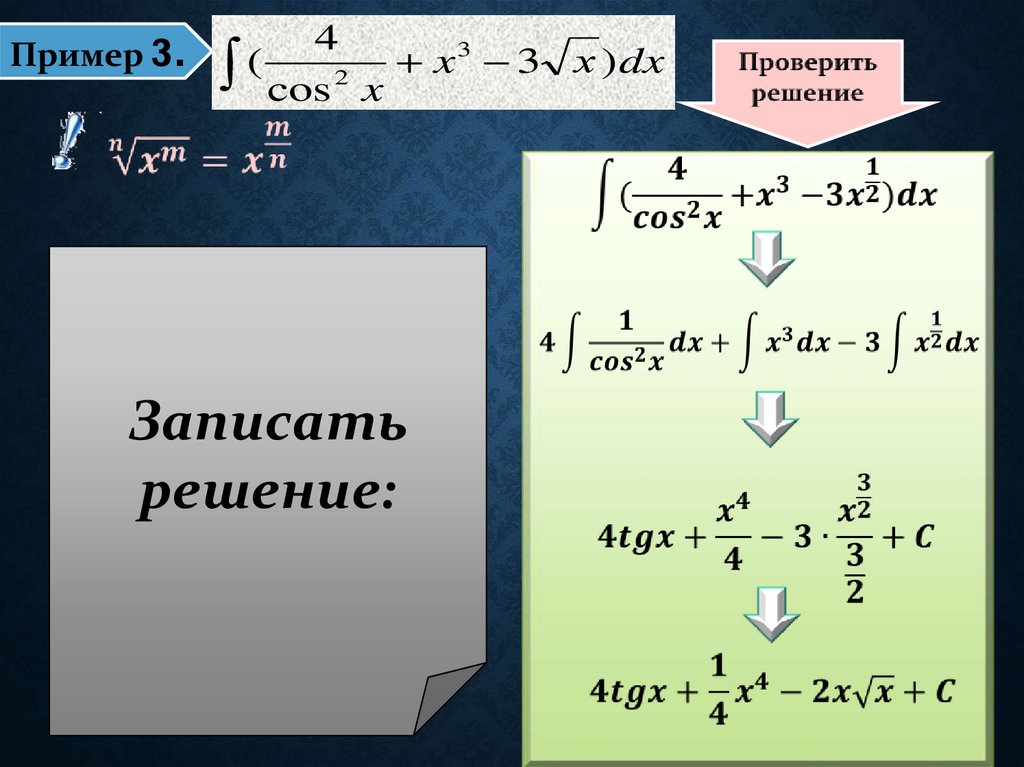
16.
Пример 3.4
3
(
x
3 х ) dx
cos 2 x
Записать
решение:
17.
sin( 6 x 2)dxВведем новую переменную и
выразим дифференциалы:
Записать
решение:
18.
Пример 5.3 6 x dx
Записать
решение:
Проверить
решение
19.
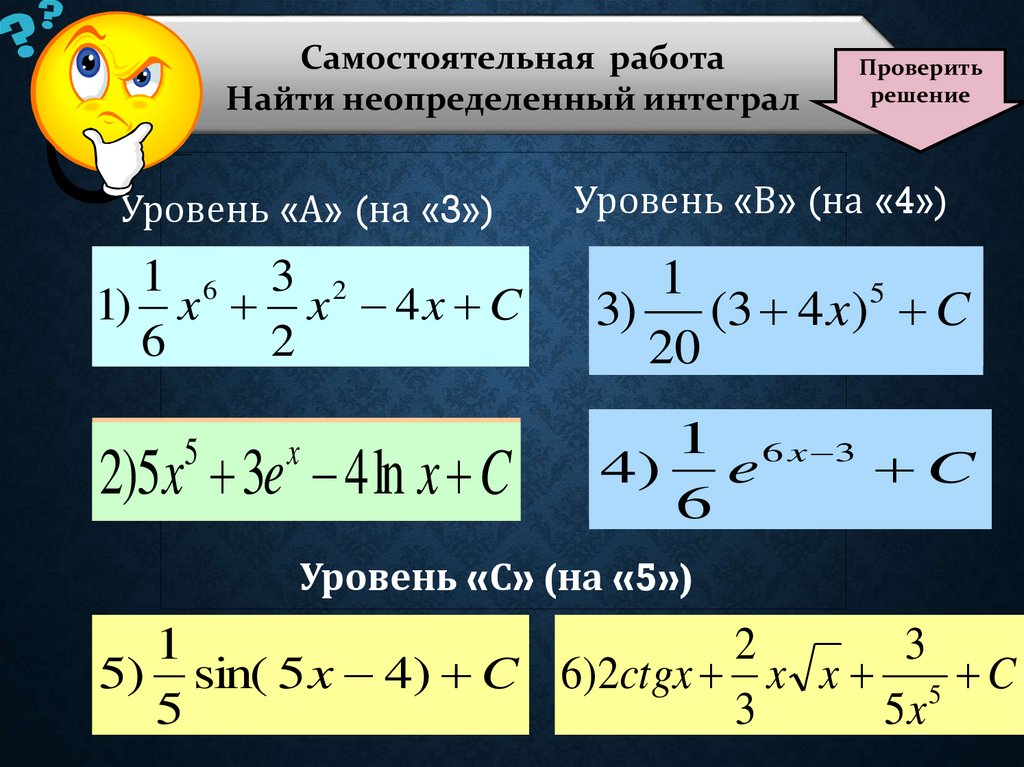
Cамостоятельная работаНайти неопределенный интеграл
Уровень «А» (на «3»)
Проверить
решение
Уровень «В» (на «4»)
1 65 3 2
1
1). (xх 3xх 44x) dxC
6
2
1
54
33). (3
(3 4
4 xõ)) dx
C
20
2)5x 3e 4 ln x C
3
1 66xx 3
4). e
dx
4
e
C
6
4
4
х
5
x
2. ( 25 х 3е ) dx
х
Уровень «С» (на «5»)
1
22
3 6
5
sin( 55xx 44
) ) dx
C 66).2 ctgx
( 2 x xõ 3õ5 )dx
C
5). cos(
5
sin 3x
5x
20.
ЗаданиеУстановить соответствие. Найти такой общий вид
первообразной, которая соответствует заданной
функции.
x
1. F x cos x C
2
3
1. f x x x
x2
x4
2. F ( x )
C
2
4
2. f x 2 cos x
5 x 2 10 x 3
3.F ( x ) 8 x
C
2
3
2
4. F ( x ) 2 sin x C
3. f x 8 5 x 10 x
4. f x 4 3x
9
10 x 2
5.F ( x ) 8 x sin x
C
3
1
10
6. F ( x )
4
3
x
C
30
1
10
7. F ( x ) 4 3 x C
3
















 Математика
Математика








