Похожие презентации:
Решение иррациональных уравнений
1.
2. Решение иррациональных уравнений
3.
• Определение. Уравнение, содержащеепеременные под знаком корня или
дробной степени, называют
иррациональными.
4. Основные свойства
a2 x , a 02
x x; a x
a 2 x , a 0
5. Формулы сложных радикалов
A BA A2 B
2
A A2 B
, B 0, A B
2
A B
A A2 B
2
A A2 B
, B 0, A B
2
6. Формулы сокращенного умножения
A B1. A B
A B
A B
2. A B
3. 3 A 3 B
4. 3 A 3 B
, A 0, B 0, A2 B 2 0;
, A 0, B 0, A B;
A B
A B
3
3
A2 3 AB 3 B 2
A B
A2 3 AB 3 B 2
, A2 B 2 0
, A2 B 2 0;
7. Равносильные переходы
f ( x) g 2 ( x)f ( x) g ( x)
g ( x) 0
f ( x) g ( x)
f ( x) g ( x)
f ( x) g ( x)
f ( x) 0
g ( x) 0
8. Методы решения
• 1.Возведение в степень• 2.Метод замены
• 3.Метод тригонометрической
подстановки
• 4.Умножение обеих частей уравнения
• 5.Специальные методы
9. Возведение в степень
1. x 5 x 1 2 x 12
2. x x 1 2 x 2
2
2
3. x 2 x 3 2
4. 5 x 7 2 x 3 3 x 4
5. 2 x 1 x 2 2 x 4 x 1
Выполнить № 1, 2, 4
№ 3, 5- домашнее задание
10. Метод замены
1. 3 x 5 x 2 12. x 3 8 4 x 3 8 6
3. 3 x 5 x 8 . 3 x 5 x 1 1
2
2
4. 2 x 3 x 1 3 x 2 2 x 2 5 x 3 16
5.3 x 2 x 2 4 x x 2 0
6. x 5 4 x 1 x 2 2 x 1 1
7. x 3 x 2 1 x 3 x 2 2 3
Выполнить № 1, 3,4, 6
№ 2, 5, 7- домашнее задание
11. Тригонометрическая подстановка
1.x a sin t
Если в уравнение входит
a2 x2
x a cos t
2.
3.
x atgt
1
x
sin t
Если в уравнение входит
Если в уравнение входит
a2 x2
12.
Тригонометрическая подстановка1. x 1 x
2
2.x
5
2 x 1
x
35
2
x 1 12
2
Выполнить № 1
№ 2- домашнее задание
13.
Метод умножения.
Домножение на
3)
x2 9
x 4
x 4
2
4)
x 9
3
g x
1
x 4
x2 8x
x 9
;
3
x 9
.
Выполнить № 3
№ 4- домашнее задание
14.
Метод умноженияДомножение на «сопряженное»
1. x 3 x 6 x 3 x 3 3
2
2
2. 5 x 7 x 4 4 x 3
2 x 2 x
2
3.
2 x 2 x x
15. Метод умножения
Выполнить дома:5)
x 3 x 2 2
;
9
x 1 x 2
1
4
1
3
6)
.
2
2
x x x x x x x
16. Специальные методы
1. ОДЗ7)
8)
x 4 1
3 x 2 x 2 x 42;
x 2 4 x 3 x 2 3x 2 x 2 x .
Выполнить № 7
№ 8- домашнее задание
17.
Использование монотонности:1) 3 3 5 x 3 x 1 2;
2) 7 3x 5 4 x 1 2 x 2;
3) 2 x 1 1
2 x 1 7 x 1 x 2 7 0;
2
Выполнить
№ 1, 3, 4
№ 2, 5, 6домашнее
задание
4) 3x 2 x 2 3 3x 18 2 3 x 18 2 ;
3 2 x 2 3x 4
2x 5
5)
;
2
5 3 x 3x 4 3x 8
6)
x 2 2 x 1 3
x 6 4
x 6 2 x 1 3
x 2
18.
f f f x xУравнения
2вида: 2
2
1) x 4 x 2 4 x 4 x 2 2 x;
2) x 5 5 ... 5 x ;
Выполнить
№
1,
3,
3) x 4 x 2 6 8 3 8 x 7 x 3 7 0; № 2, 4, 5домашнее
4
задание
2 x
4)
2 2 x 1
x;
5) x 9 6 x 6 12 x 3 6 3 2 x .


















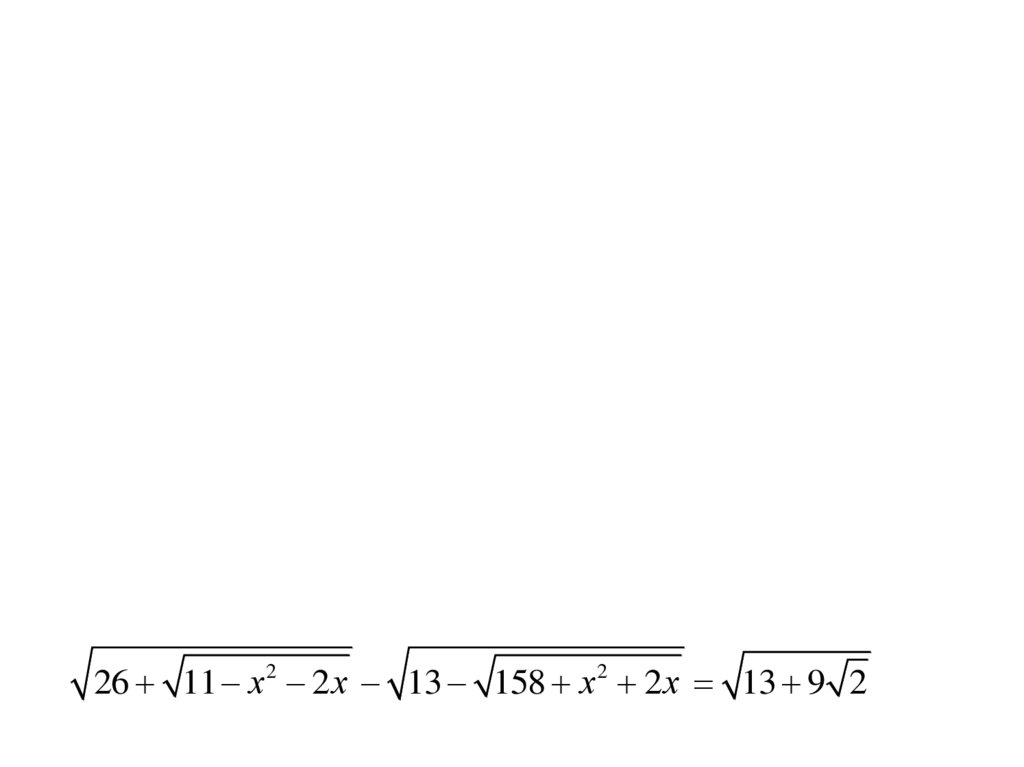
 Математика
Математика








