Похожие презентации:
Вычисление интегралов различными методами
1. Вычисление интегралов различными методами. Применение определенного интеграла к вычислению площади плоской фигуры
2.
Функция F(x) называетсяпервообразной для функции f(x) на
интервале X=(a,b) (конечном или
бесконечном), если в каждой точке этого
интервала f(x) является производной для
F(x), т.е.
3.
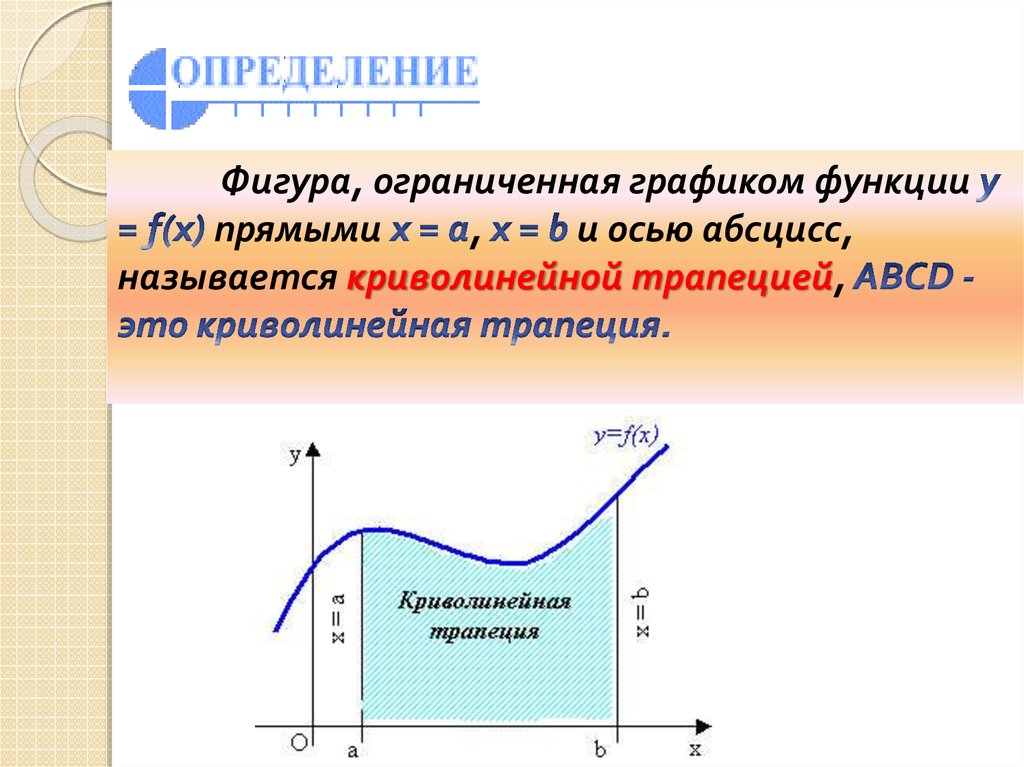
Фигура, ограниченная графиком функциипрямыми
,
и осью абсцисс,
называется криволинейной трапецией,
4.
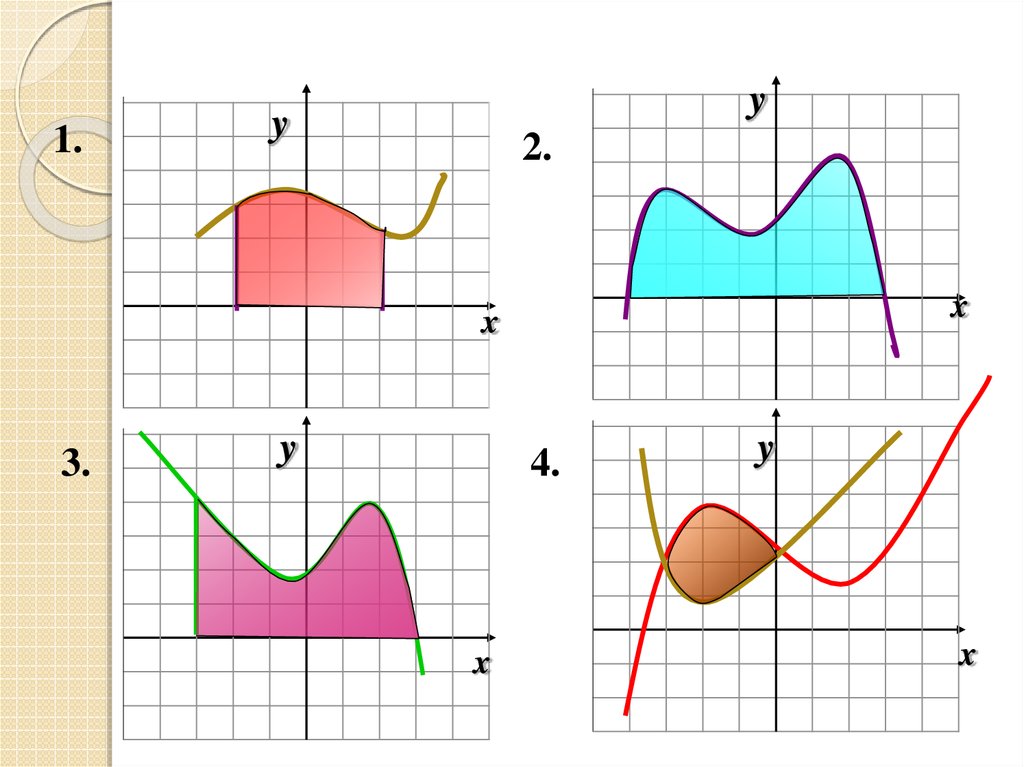
1.y
y
2.
x
x
3.
y
4.
x
y
x
5.
- это предел, ккоторому стремится интегральная сумма
при
Обозначают:
.
6. Геометрический смысл определенного интеграла
Еслина отрезке [a; b] неотрицательна, то
b
определенный интеграл
a
f ( x)dx
, ограниченной графиком
функции f (x), осью абсцисс и прямыми
,
,т.е.
b
S f ( x)dx
a
7. Формула Ньютона- Лейбница
Если f(х) – непрерывная и неотрицательная наотрезке [a; b] функция , а F(х) – ее
первообразная на этом отрезке , то площадь S
соответствующей криволинейной трапеции
равна приращению первообразной на отрезке
[a; b] , т.е.
8. Свойства определенного интеграла
a1. f x dx 0 ;
a
b
2. dx b a ;
a
b
a
3. f x dx f x dx ;
a
b
b
4. f1 x f 2 x dx f1 x dx f 2 x dx ;
a
b
b
a
a
9. Свойства определенного интеграла
bb
a
b
a
5. Kf x dx K f x dx ;
c
b
a
c
6. f x dx f x dx f x dx ;
a
b
7. f x dx 0 , если f x 0 .
a
10. Таблица интегралов
1. dx x C ;n 1
x
2. x n dx
C n 1 ;
n 1
dx
3.
ln x C ;
x
x
a
4. a x dx
C;
ln a
5. e dx e C ;
x
x
6. sin x dx cos x C ;
7. cos x dx sin x C ;
dx
8.
tg x C ;
2
cos x
dx
ctg x C ;
2
sin x
dx
1
x a
10. 2
ln
C;
2
x a
2a x a
9.
11.
12.
dx
x2 a2
dx
ln x x 2 a 2 C ;
arcsin
x
C;
a
a2 x2
dx
1
x
13. 2
arctg C.
2
x a
a
a
11. Примеры:
80
4/3
3
3x
x dx
4
8
0
3 3
x x
4
2
1 2x
1 e dx 2 e
2x
3
3
3
4
x
3
3
(
x
1
)
dx
x
1
1 dx 1 dx 4
2
1
8
0
3 3
(8 8 0) 12
4
1 4
1 2 2
2
(e e ) e (e 1)
2
2
4
4
x
3
1
1
3
3
3
3
x
(
x
)
(
3
)
(
1
)
(
20
3
)
24
1
1
1
4
4
4
4
4
12. Пример
3e
Вычислить
0
x
3
e 3 dx
1
3 x
e 3 dx
0
0
3 e
1
x
3 dx
.
1
x
3e 3
3
0
1
1 3
0
3 e 3 e 3
1 e
1
1 3 1 3
e
e
13. Интегрирование методом подстановки.
14.
Теорема (Замена переменной вопределенном интеграле).
Пусть f x непрерывна на a, b , а
функция x t непрерывна вместе
со своей производной t на
отрезке , , причем a ,
b . Тогда
b
a
f x dx f t t dt .
15. Пример
x 1 tx 1 t 2
2
t
1
2
x t 1, dx 2tdt
2tdt
t
1
x 1
x 0, t 1
3
2
xdx
0
x 3, t 2
2
t
8 1
2 t 1 dt 2 t 1 dt 2
t 2 2 1
3
1
1
3 3
1
2
2
2
2
3
1
4 8
8
7
2 2 1 2 1 2
3
3 3
3
3
16. Интегрирование по частям
17.
Теорема (Интегрирование по частям вопределенном интеграле).
Если функции u u x , v v x и их
производные u x и
v x непрерывны на отрезке a, b , то
b
b
a
a
b
udv u v vdu .
a
18.
Примерdx
u ln x, du
e e dx
x x ln x 1 x
ln xdx
x
1
1
dv dx, v x
e
x ln
e
x1
e
e
dx e ln e ln 1 x 1
1
e e 1 1
19. Применение определенного интеграла для вычисления площадей плоских фигур
20.
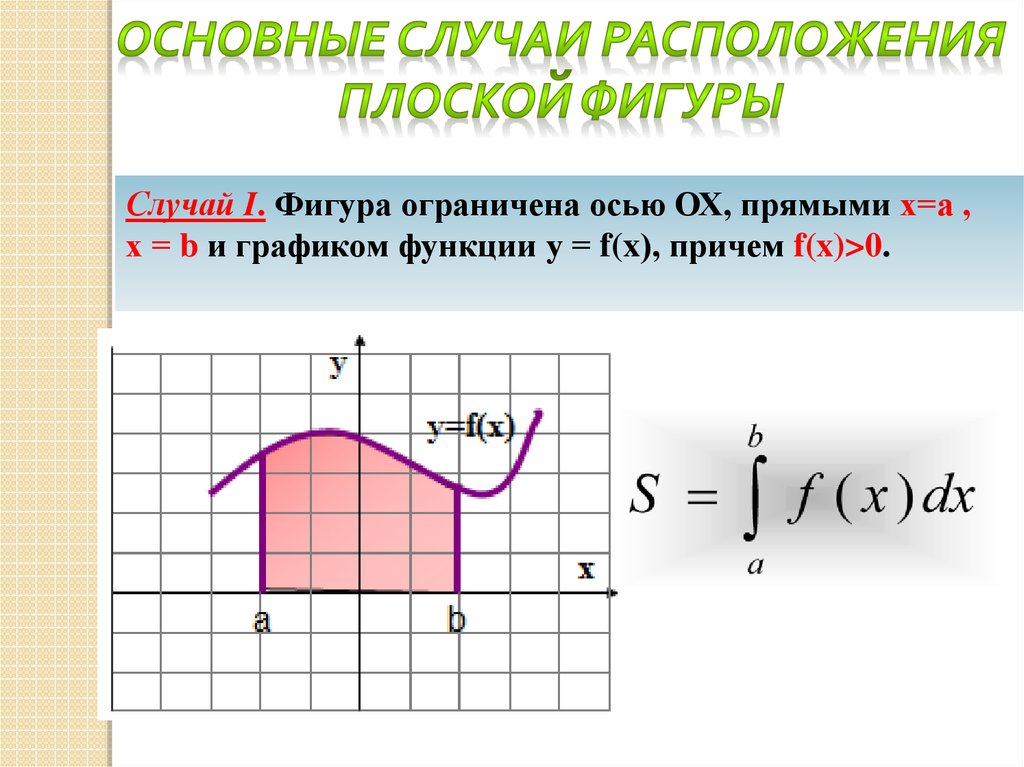
Случай I. Фигура ограничена осью ОХ, прямыми х=а ,х = b и графиком функции у = f(x), причем f(x)>0.
21.
Случай II. Фигура ограничена осью ОХ, прямыми х=а,х = b и графиком функции у = f(x), причем f(x)<0.
b
S
f ( x)dx , f ( x) 0
a
22.
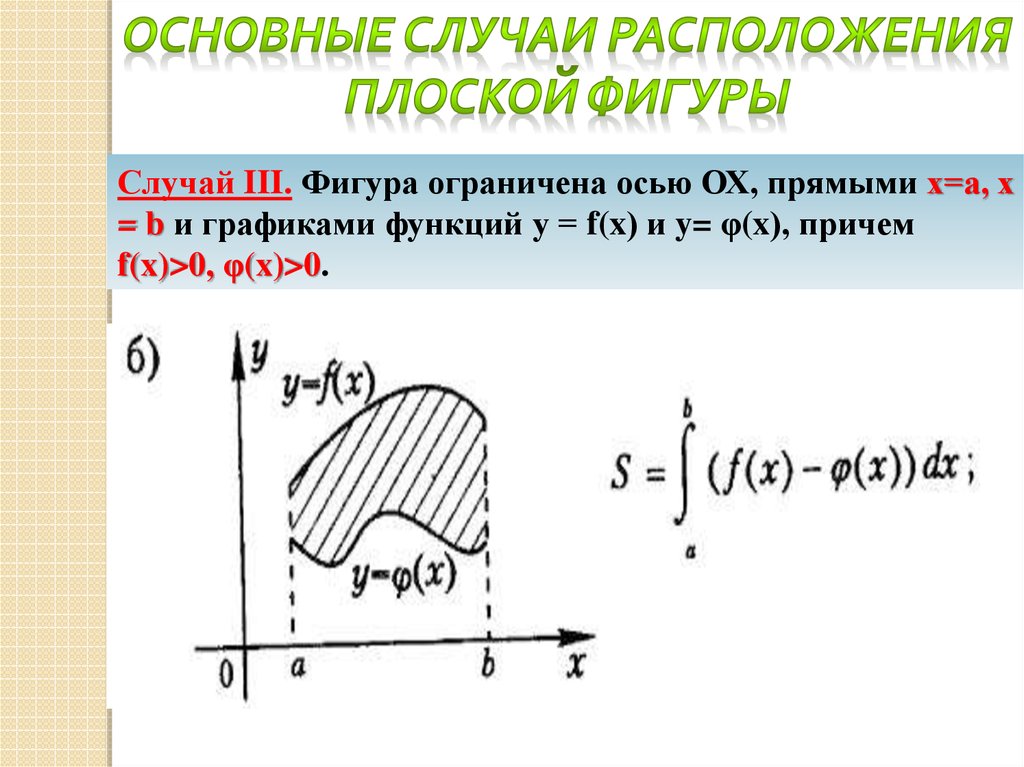
Случай III. Фигура ограничена осью ОХ, прямыми х=а, х= b и графиками функций у = f(x) и y= φ(x), причем
f(x)>0, φ(x)>0.
23.
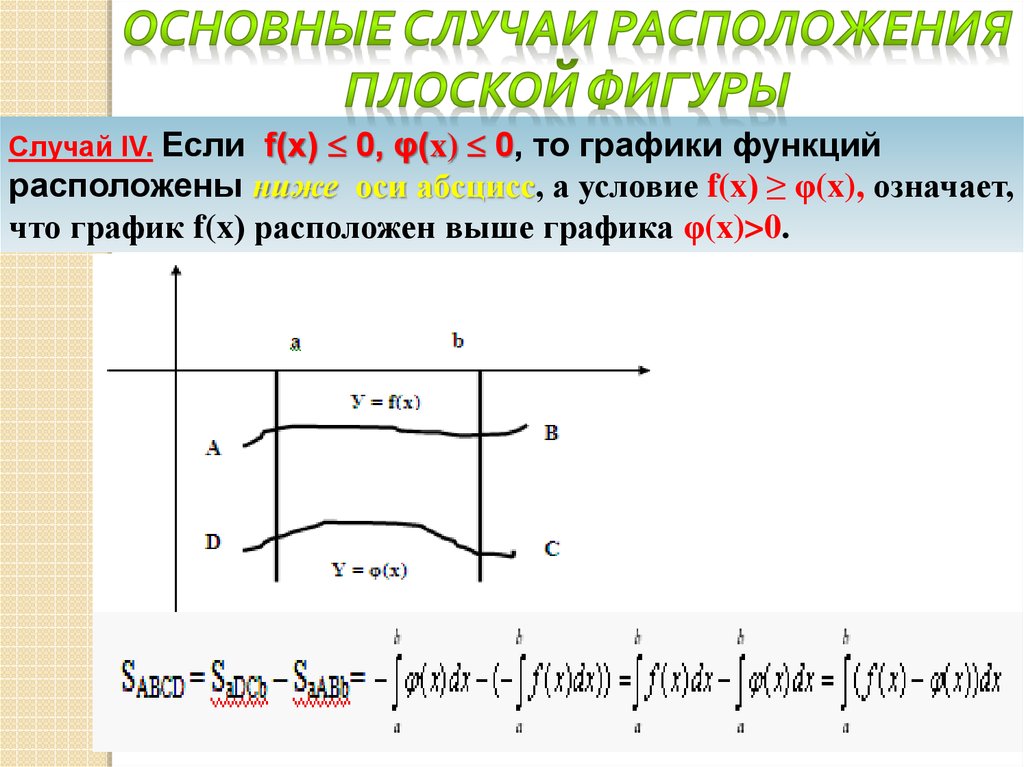
Случай IV. Если f(x) 0, φ(x) 0, то графики функцийрасположены ниже оси абсцисс, а условие f(x) ≥ φ(x), означает,
что график f(x) расположен выше графика φ(x)>0.
24.
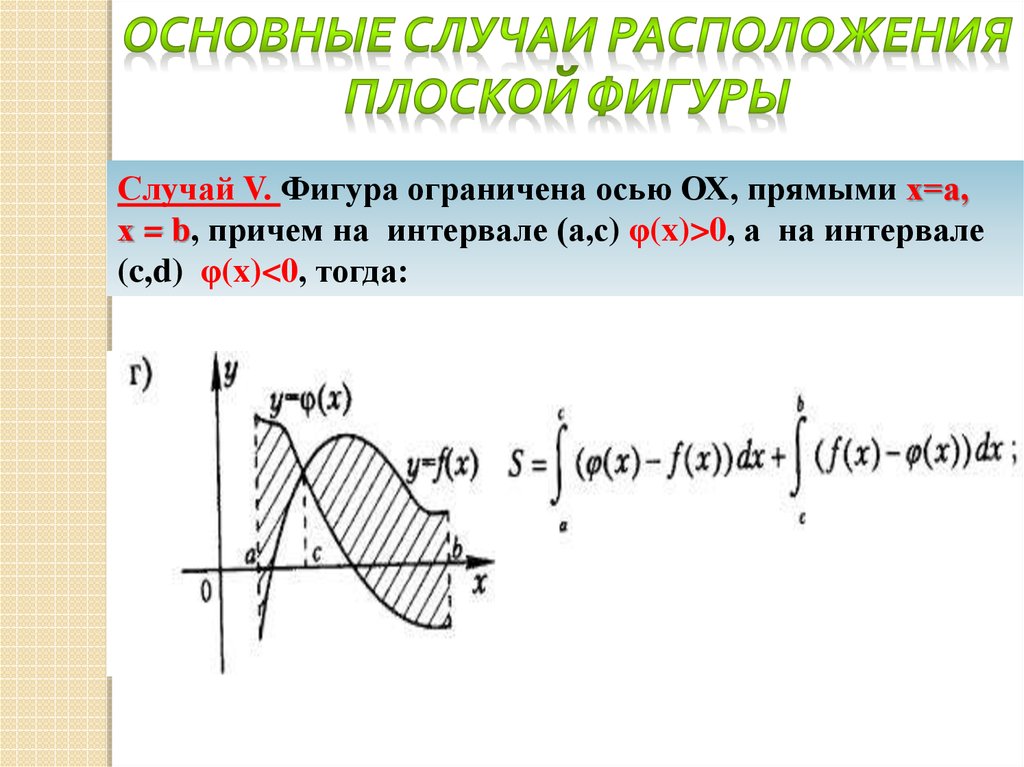
Случай V. Фигура ограничена осью ОХ, прямыми х=а,х = b, причем на интервале (а,с) φ(x)>0, а на интервале
(c,d) φ(x)<0, тогда:
25.
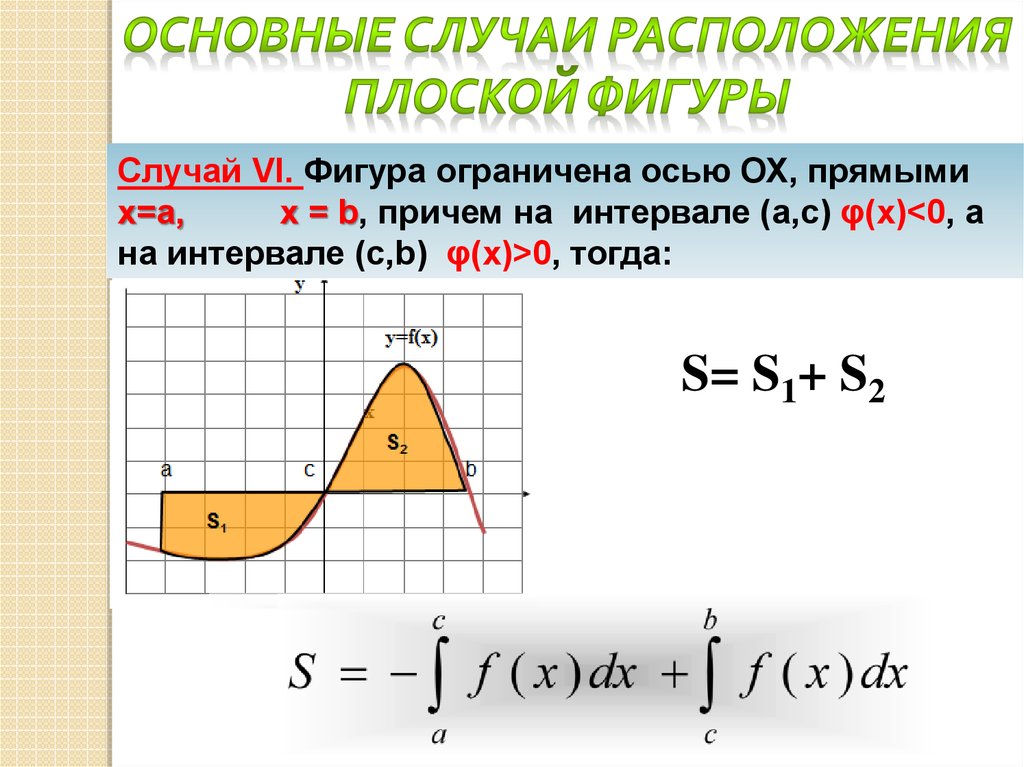
Случай VI. Фигура ограничена осью ОХ, прямымих=а,
х = b, причем на интервале (а,с) φ(x)<0, а
на интервале (c,b) φ(x)>0, тогда:
S= S1+ S2
26.
1.Сделать чертеж графиков заданныхфункций, ограничивающих площадь
плоских фигур.
2.Найти пределы интегрирования.
3.Выяснить какой формулой площади
плоской фигуры удобно пользоваться в
данном случае.
4.Вычислить площадь заданной фигуры.
27.
Пример. Найдите площадь фигуры,ограниченной линиями у = х - 3, у = х2 -3
у
х
-2
5
S 11
6
3
у = х2 - 3
28.
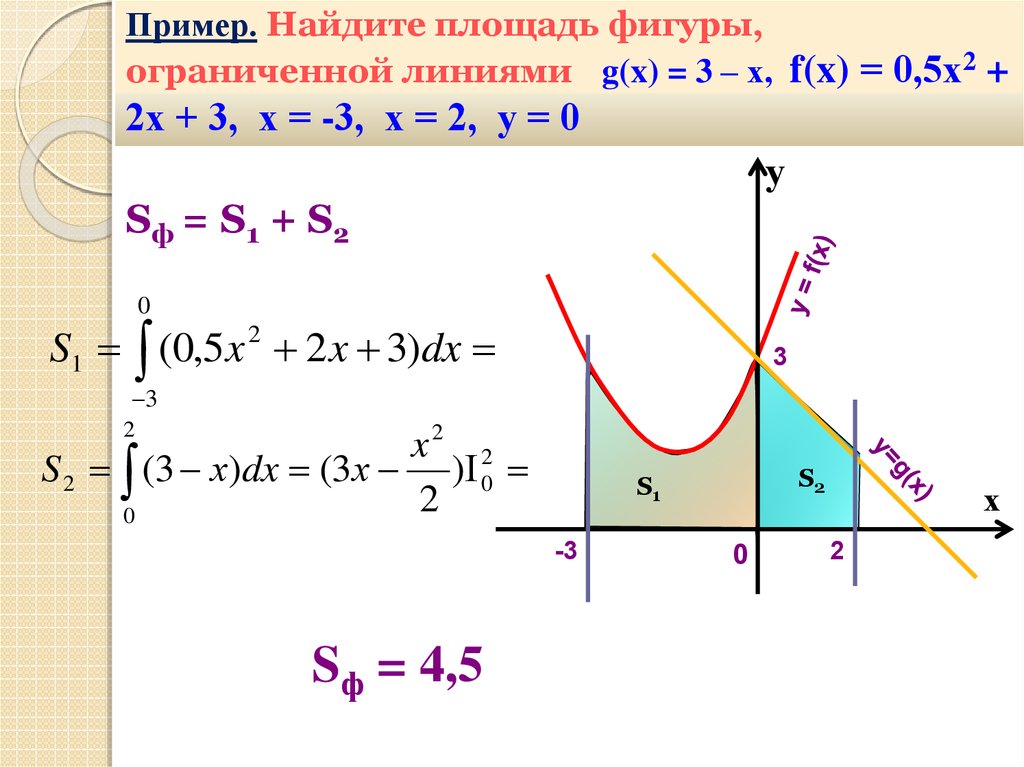
Пример. Найдите площадь фигуры,ограниченной линиями g(x) = 3 – х, f(x) = 0,5х2 +
2х + 3, х = -3, х = 2, у = 0
у
Sф = S1 + S2
0
S1 (0,5x 2 2 x 3)dx
3
3
2
x2 2
S 2 (3 х)dx (3х ) 0
2
0
-3
Sф = 4,5
S2
S1
0
х
2
29.
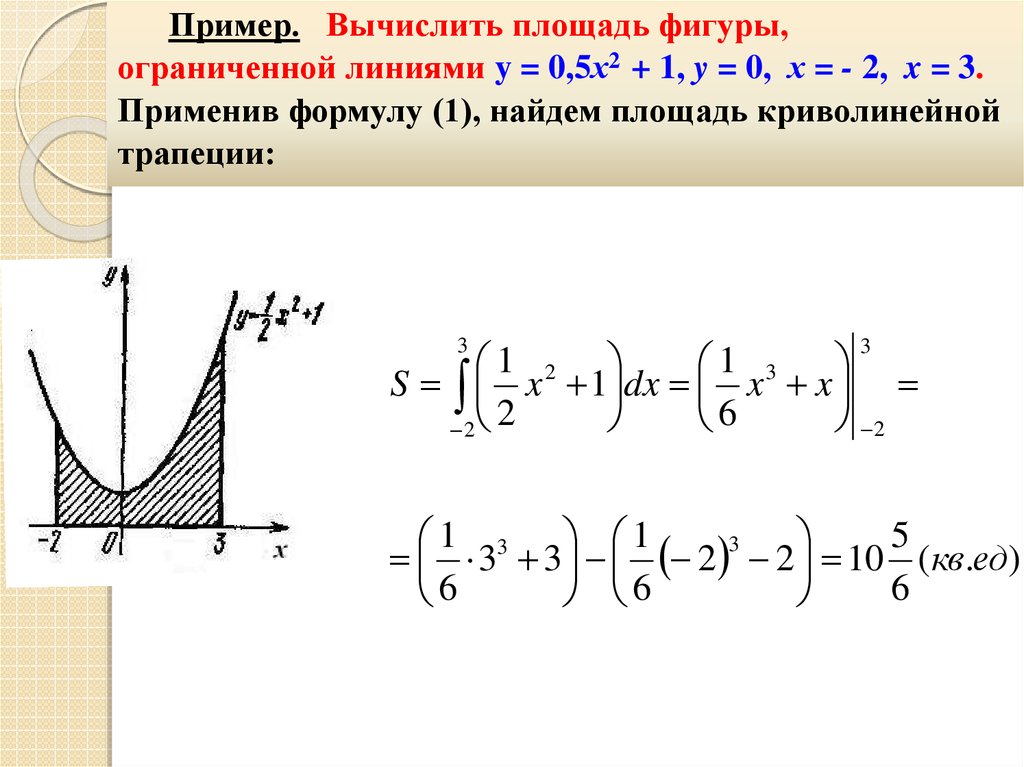
Пример. Вычислить площадь фигуры,ограниченной линиями y = 0,5х2 + 1, y = 0, х = - 2, x = 3.
Применив формулу (1), найдем площадь криволинейной
трапеции:
3
1 2
1 3
S x 1 dx x x
2
6
2
2
3
5
1 3
1
3
3 3 2 2 10 (кв.ед)
6
6
6
30.
Пример. Вычислить площадь фигуры,ограниченной линиями y = - х2 - 1, у = 0, х =-1, х = 2.
По формуле (2) находим
2
S x 2 1 dx
1
x
2
2
1 dx
1
2
1 3
1 3
1
3
x x 2 2 1 1 6(кв.ед)
3
1 3
3
31.
Пример . Вычислить площадь фигуры,ограниченной линиями у = sin х, y = 0, х = -π/2, х = π .
Очевидно, что sin х ≤ 0 для
всех х ∈ [- π /2; 0] и sin х ≥ 0
для всех х ∈ [0; π].
Поэтому
0
S sin xdx sin xdx cos x
2
0
0
2
cos x
0
cos 0 cos cos cos 0 1 0 1 1 3(кв.ед)
2
32.
Пример . Вычислить площадь фигуры,ограниченной1
1
линиями y x 2 и y x 2 .
3
9
Пределы интегрирования а и b находим из системы уравнений:
1
y
x 2,
3
y 1 x2.
9
1
1
Отсюда 3 x 2 9 x , т. е. x2 - Зх - 18 = 0, откуда х =
- 3 и х = 6. Следовательно, а = - 3 и b = 6 . Так как на
отрезке [- 3; 6] для f ( x) 1 x 2, g ( x) 1 x 2 .
3
9
2
имеем f(x) ≥ g(x), то по формуле (3) находим
6
1
1
1
1
S x 2 x 2 dx x 2 2 x x 3
3
27 3
9
6
3
6
1 3 1
1
1 2
2
3
6 2 6 6 3 2 3 3 13,5(кв.ед)
27 6
27
6
33.
ОТВЕТ34.
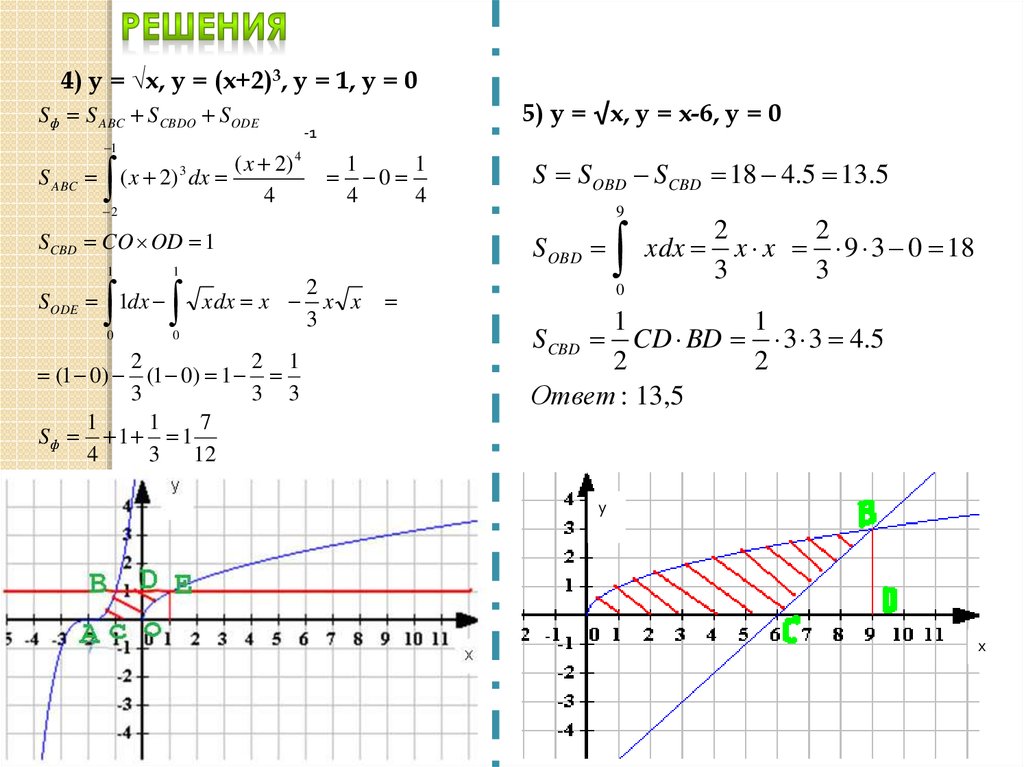
4) у = √х, у = (х+2)3, у = 1, у = 0S ф S ABC S CBDO S ODE
1
S ABC
( x 2) 4
( x 2) dx
4
3
2
S CBD CO OD 1
1
S ODE 1dx
0
5) у = √х, у = х-6, у = 0
-1
1
1
1
0
4
4
-2
S S OBD S CBD 18 4.5 13.5
S OBD
1
1
0
2
x dx x x x
3
0
2
2 1
(1 0) (1 0) 1
3
3 3
1
1
7
Sф 1 1
4
3 12
0
9
9
0
xdx
2
2
x x 9 3 0 18
3
3
0
1
1
S CBD CD BD 3 3 4.5
2
2
Ответ : 13,5
у
х
35.
Вычислить площади фигур, ограниченныхлиниями.
1) у = 5 - х2, у = 3 - х
а) 3
б) 4,5 в) 6
г) 6,5
2) у = 4х – х2, у = 0
а) 3 2/3 б) 11
в) 9 ½
г) 10 2/3
3) у = х3, у = х
а) 1 ¼
б) ½
г) 1 ½
в) ¼
4) у = 1/(х – 1)2, у = 0, х = -1, х = 0
а) 0,75
б) 1
в) 0,5 г) 1,25
ОТВЕТ
36. Ответы
1–б2–г
3–в
4–в
Назад к заданиям
37.
38.
СПАСИБО ЗАВНИМАНИЕ!




























 Математика
Математика








