Площадь фигур. Определение первообразной

1. Первообразная

Задание №7
Площадь фигур

2. Определение первообразной

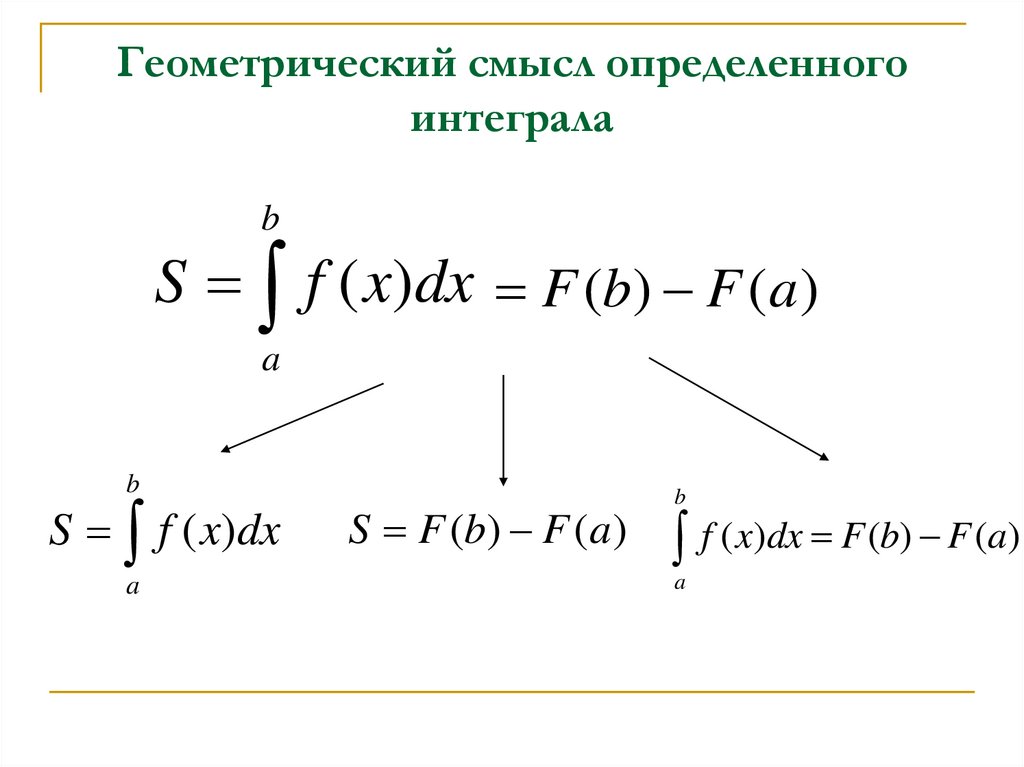
F ( x) f ( x)

3. Геометрический смысл определенного интеграла

b
S f ( x)dx F (b) F (a )
a
b
S f ( x)dx
a
S F (b) F (a )
b
f ( x)dx F (b) F (a)
a

4.

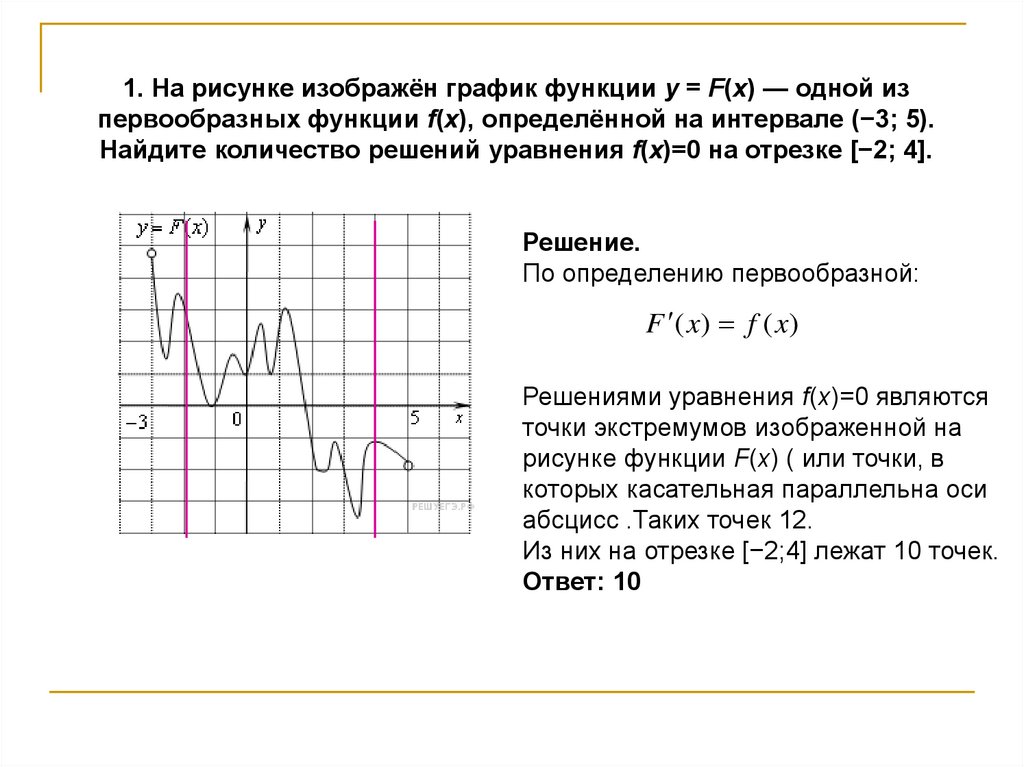
1. На рисунке изображён график функции y = F(x) — одной из
первообразных функции f(x), определённой на интервале (−3; 5).
Найдите количество решений уравнения f(x)=0 на отрезке [−2; 4].
Решение.
По определению первообразной:
F ( x) f ( x)
Решениями уравнения f(x)=0 являются
точки экстремумов изображенной на
рисунке функции F(x) ( или точки, в
которых касательная параллельна оси
абсцисс .Таких точек 12.
Из них на отрезке [−2;4] лежат 10 точек.
Ответ: 10

5.

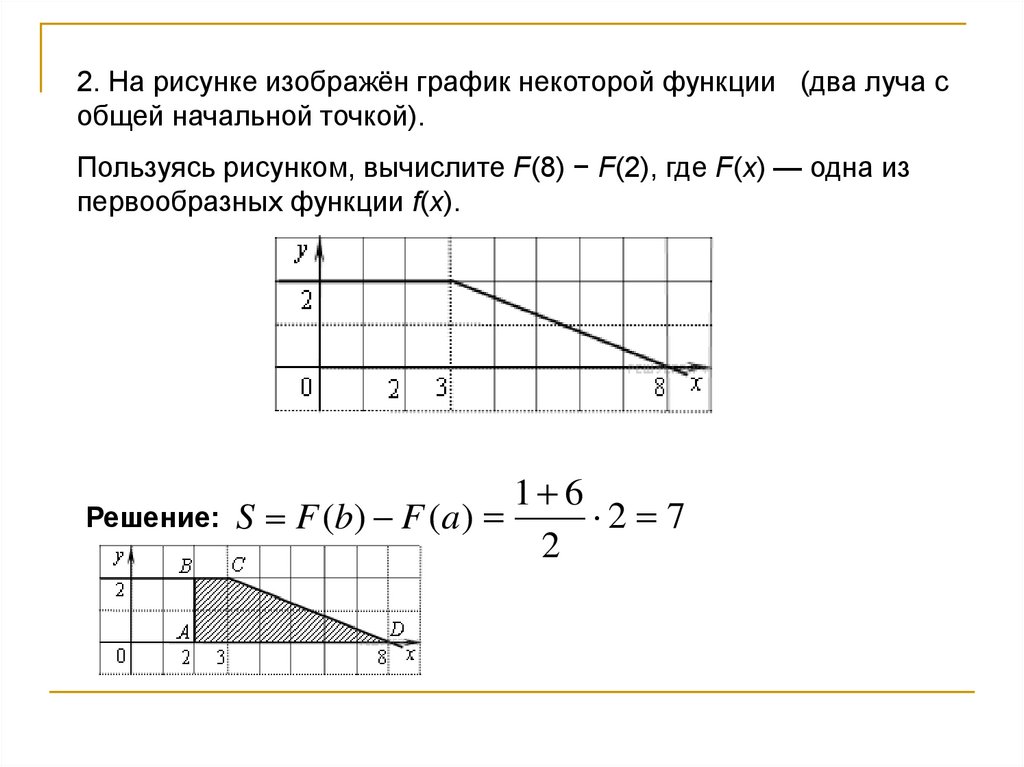
2. На рисунке изображён график некоторой функции (два луча с
общей начальной точкой).
Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из
первообразных функции f(x).
Решение:
1 6
2 7
S F (b) F (a )
2

6. 3. На рисунке изображён график функции y = f(x). Функция    одна из первообразных функции y = f(x). Найдите площадь закрашенной

3. На рисунке изображён график функции y = f(x).
3
2
Функция F ( x) x 30 x 302 x
15
8
одна из первообразных функции y = f(x). Найдите площадь закрашенной
фигуры
Решение:
S F (b) F (a )
S F ( 9) F ( 11)
Ответ: 6

7.

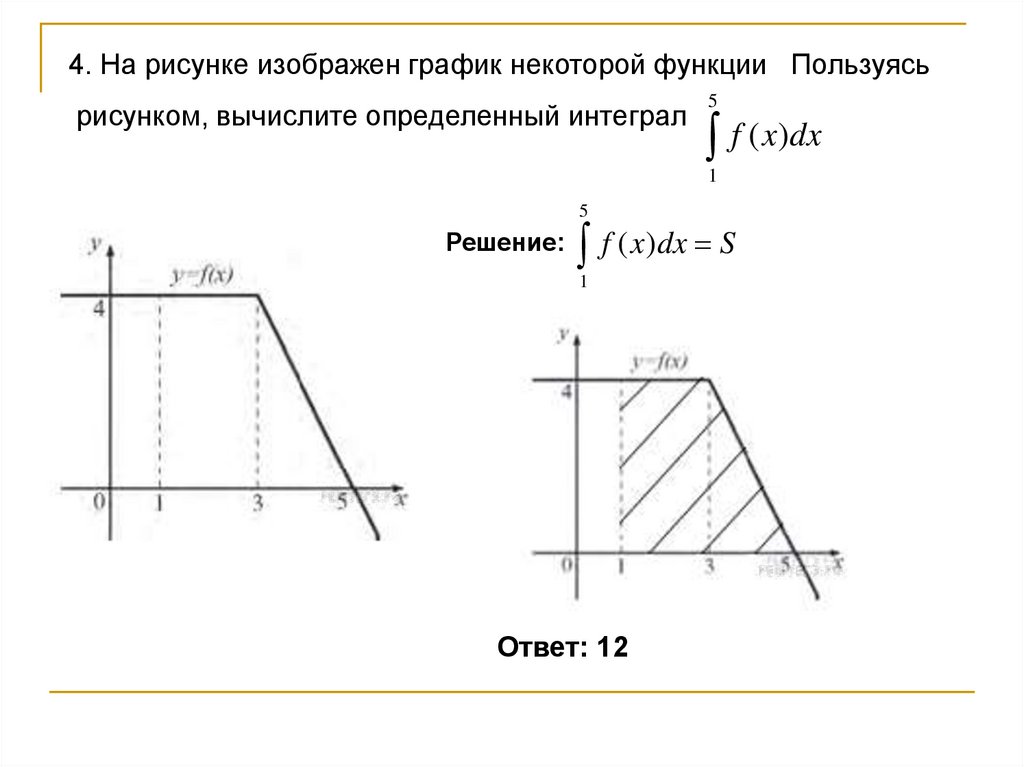
4. На рисунке изображен график некоторой функции Пользуясь
рисунком, вычислите определенный интеграл
5
f ( x)dx
1
5
Решение:
f ( x)dx S
1
Ответ: 12

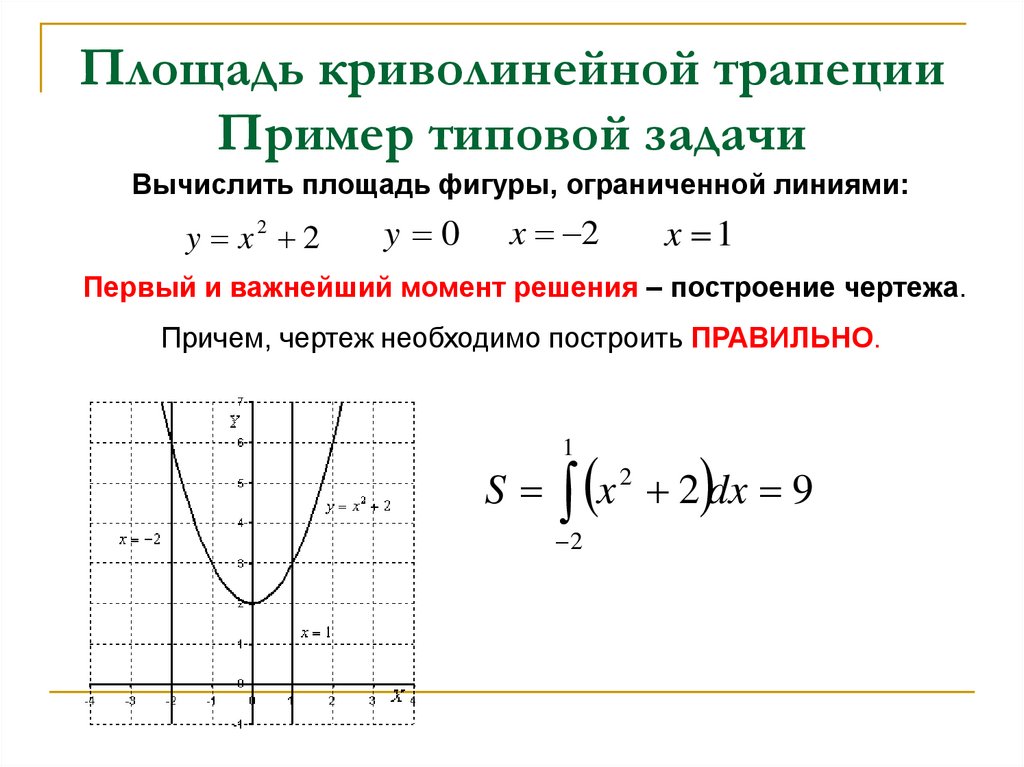
8. Площадь криволинейной трапеции Пример типовой задачи

Вычислить площадь фигуры, ограниченной линиями:
y x2 2
y 0
x 1
x 2
Первый и важнейший момент решения – построение чертежа.
Причем, чертеж необходимо построить ПРАВИЛЬНО.
x
1
S
2
2
2 dx 9

9. Нетипичное расположение фигуры

Если криволинейная трапеция
расположена под осью Ох
Если фигура расположена и в верхней и в
нижней полуплоскости
Если фигура не является криволинейной
трапецией

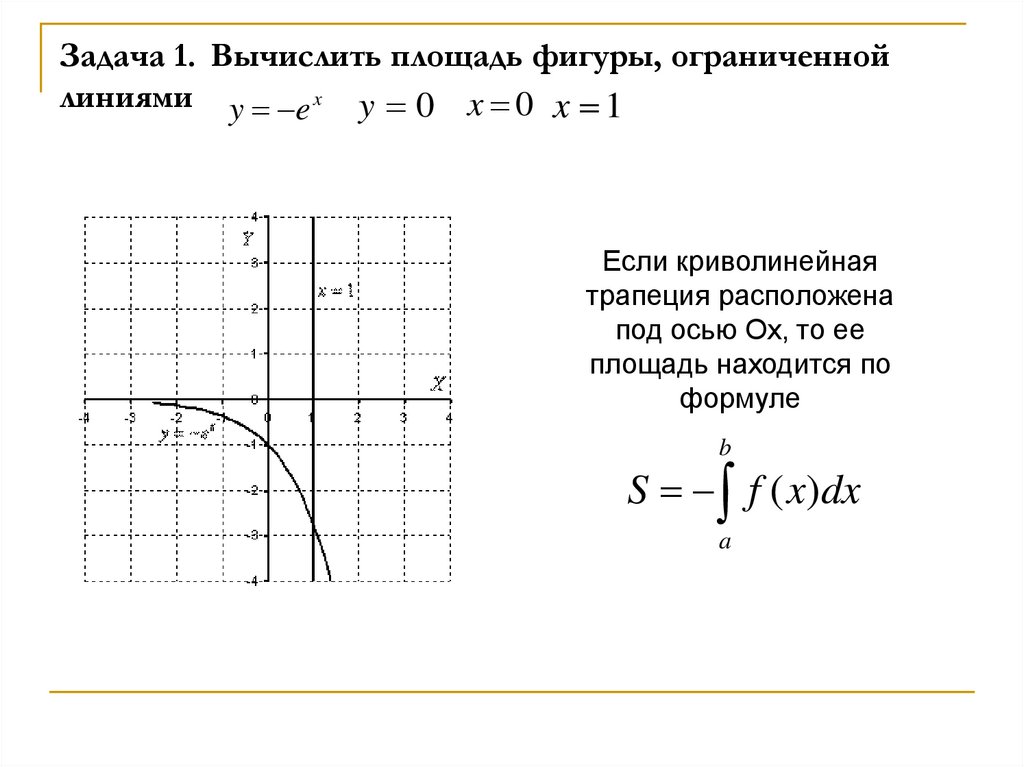
10. Задача 1. Вычислить площадь фигуры, ограниченной линиями

y e x y 0 x 0 x 1
Если криволинейная
трапеция расположена
под осью Ох, то ее
площадь находится по
формуле
b
S f ( x)dx
a

11. Внимание! Не следует путать два типа задач

Если нужно решить просто определенный
интеграл без всякого геометрического
смысла, то он может быть отрицательным.
Если предложено найти площадь фигуры
с помощью определенного интеграла, то
площадь всегда положительна! Именно
поэтому в только что рассмотренной
формуле фигурирует минус.

12.

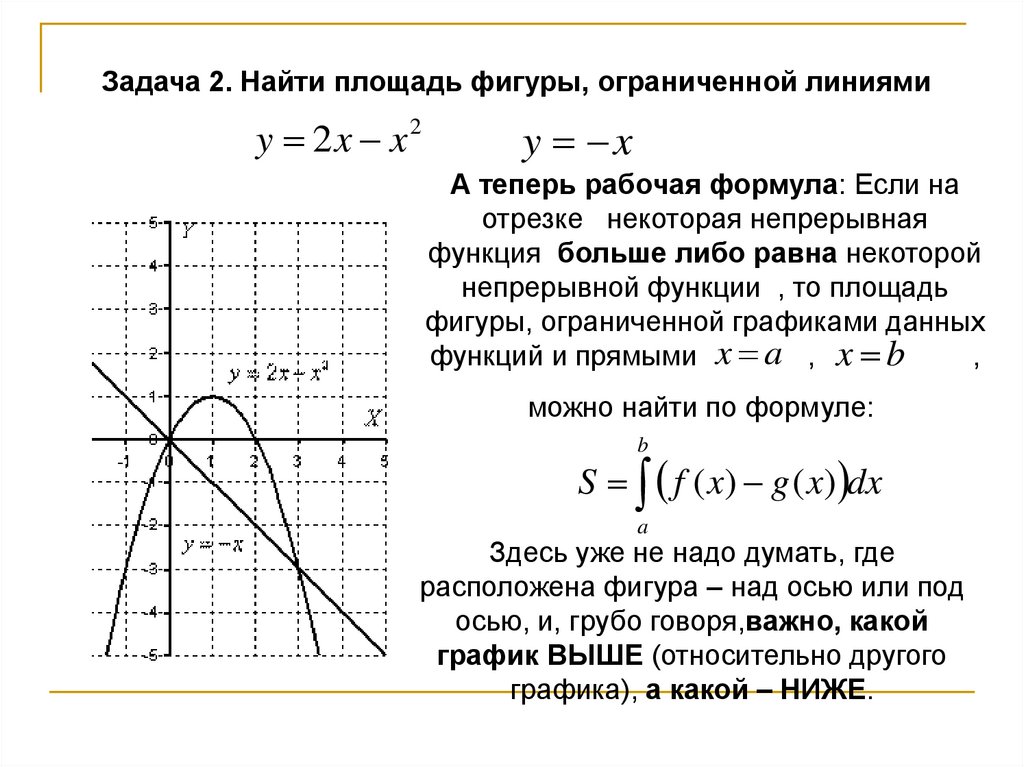
Найти площадь фигуры, ограниченной линиями
y 2x x2
y x
ВАЖНО!!!
при построении чертежа в задачах на площадь нас больше всего
интересуют точки пересечения линий. Это можно сделать двумя
способами. Первый способ – аналитический. Решаем уравнение:
2x x x
2
Этим способом лучше, по возможности, не пользоваться.
Гораздо выгоднее и быстрее построить линии поточечно, при этом
пределы интегрирования выясняются как бы «сами собой».

13.

Задача 2. Найти площадь фигуры, ограниченной линиями
y 2x x2
y x
А теперь рабочая формула: Если на
отрезке некоторая непрерывная
функция больше либо равна некоторой
непрерывной функции , то площадь
фигуры, ограниченной графиками данных
функций и прямыми x a , x b
,
можно найти по формуле:
b
S f ( x) g ( x) dx
a
Здесь уже не надо думать, где
расположена фигура – над осью или под
осью, и, грубо говоря,важно, какой
график ВЫШЕ (относительно другого
графика), а какой – НИЖЕ.

14.

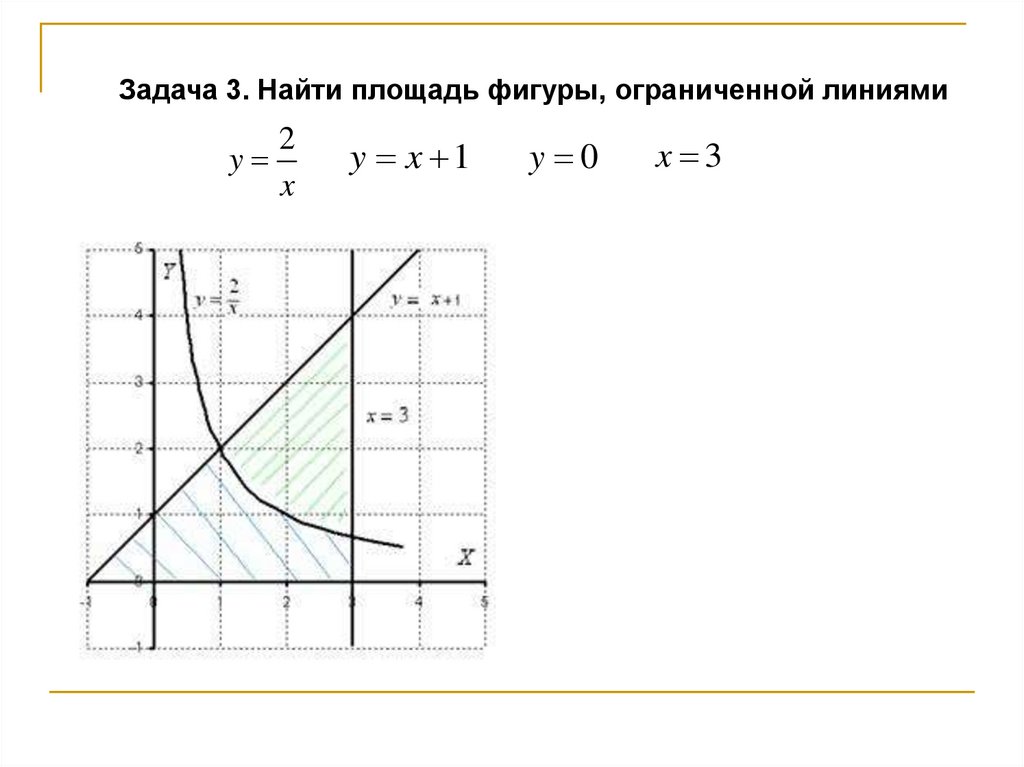
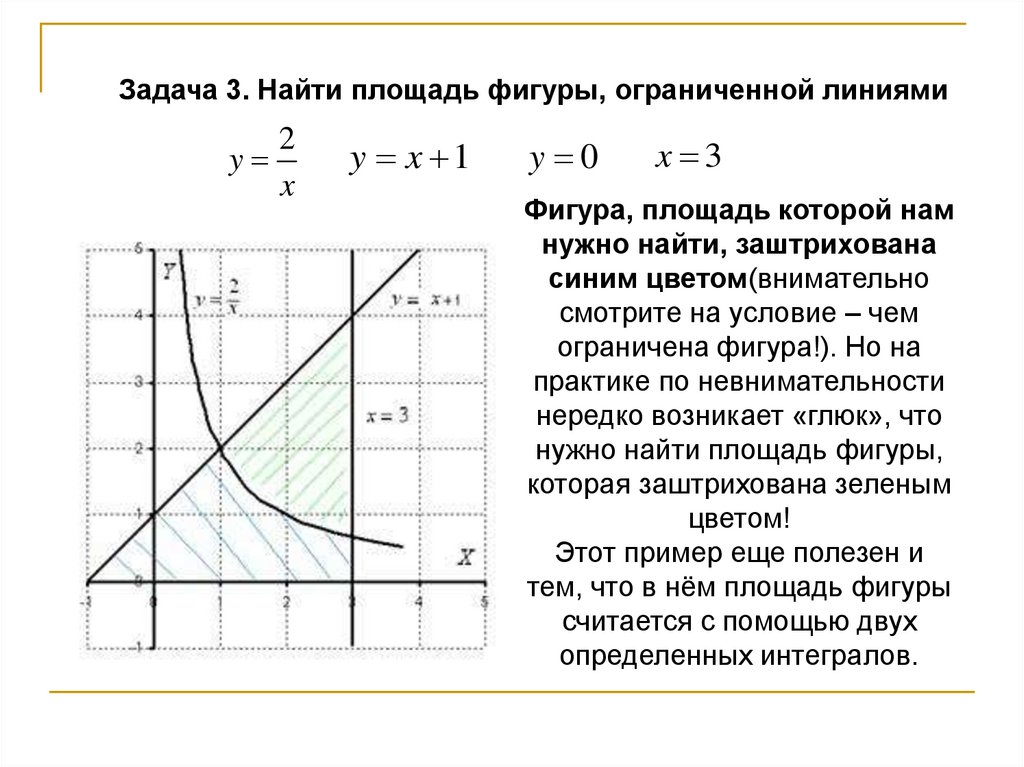
Задача 3. Найти площадь фигуры, ограниченной линиями
2
y
x
y x 1
y 0
x 3

15.

Задача 3. Найти площадь фигуры, ограниченной линиями
2
y
x
y x 1
y 0
x 3
Фигура, площадь которой нам
нужно найти, заштрихована
синим цветом(внимательно
смотрите на условие – чем
ограничена фигура!). Но на
практике по невнимательности
нередко возникает «глюк», что
нужно найти площадь фигуры,
которая заштрихована зеленым
цветом!
Этот пример еще полезен и
тем, что в нём площадь фигуры
считается с помощью двух
определенных интегралов.

16.

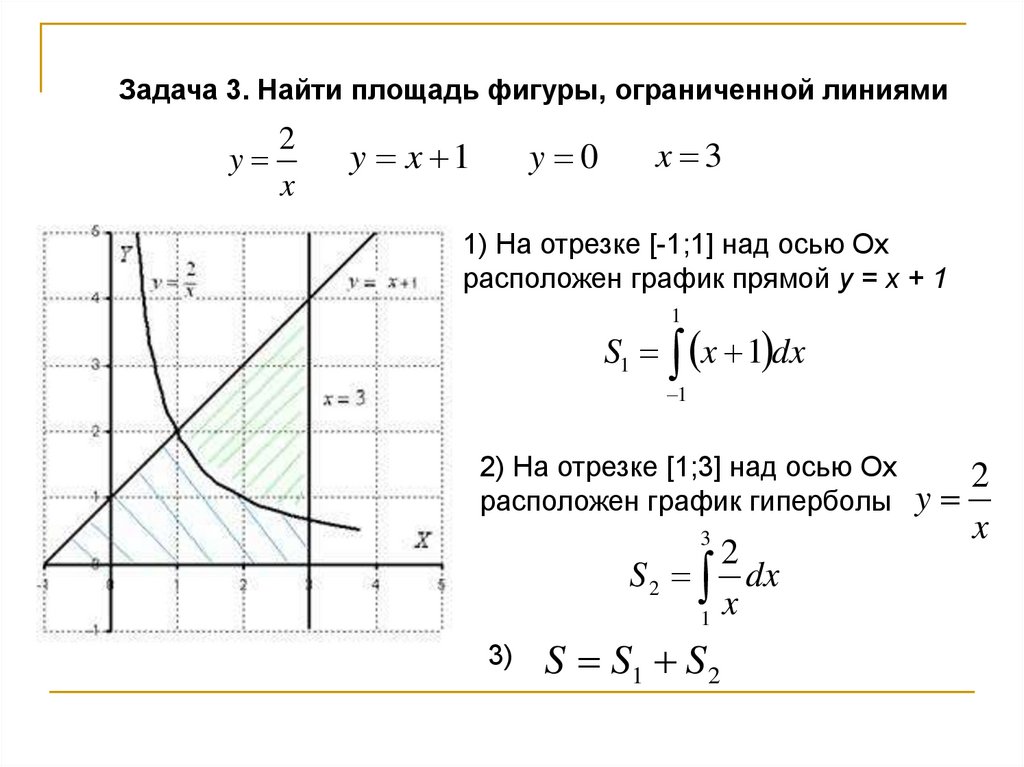
Задача 3. Найти площадь фигуры, ограниченной линиями
2
y
x
y x 1
y 0
x 3
1) На отрезке [-1;1] над осью Ох
расположен график прямой у = х + 1
1
S1 x 1 dx
1
2) На отрезке [1;3] над осью Ох
расположен график гиперболы
3
2
S 2 dx
x
1
3)
S S1 S 2
2
y
x