Похожие презентации:
Парабола c проколотой точкой. Часть II
1.
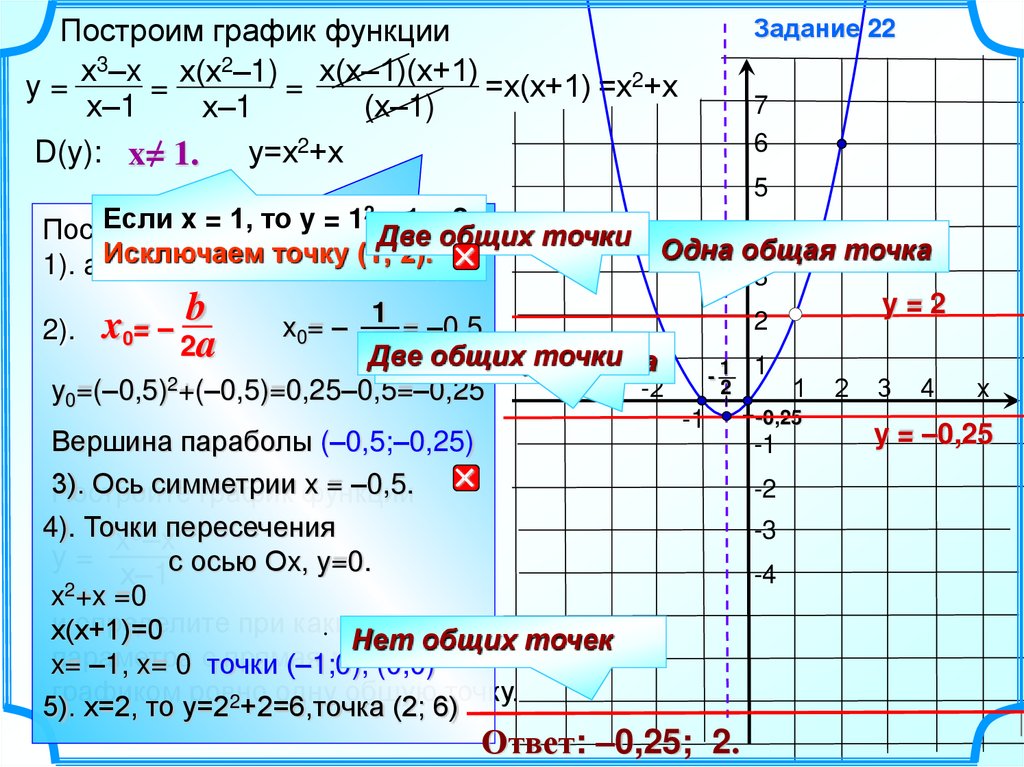
Построим график функциих3–x х(х2–1) х(х–1)(х+1)
y=
=
=х(х+1) =х2+х
=
х–1
(х–1)
х–1
D(y): x= 1.
у=х2+х
Задание 22
7
6
5
2+ 1 = 2
Если
x
=
1,
то
y
=
1
2
Построим график y= x +x
Две общих точки
Исключаем
точку
(1;
2).
1). a=1 > 0, ветви направ. вверх
4
Одна общая точка
3
x0= – 2ba
x0= – 1 = –0,5
2).
Одна
2Две
1 общих
точки
общая
точка
2
-3 -2
y0=(–0,5) +(–0,5)=0,25–0,5=–0,25
Вершина параболы (–0,5;–0,25)
3).
Ось симметрии
x = –0,5.
Постройте
график функции
4). Точки
x3–xпересечения
y=
с осью Оx, y=0.
х–1
x2+x =0
и определите при каких
значениях
х(х+1)=0
Нет
общих точек
параметра
с
прямая
y
=
с
имеет
с
x= –1, x= 0 точки (–1;0), (0;0)
графиком ровно одну общую точку.
5). х=2, то у=22+2=6,точка (2; 6)
y=2
2
-1
2
-1
Ответ: –0,25; 2.
1
1
-0,25
-1
-2
-3
-4
2
3
4
х
y = –0,25
2.
Задание 222
3
x 4 3x 3
x x 3
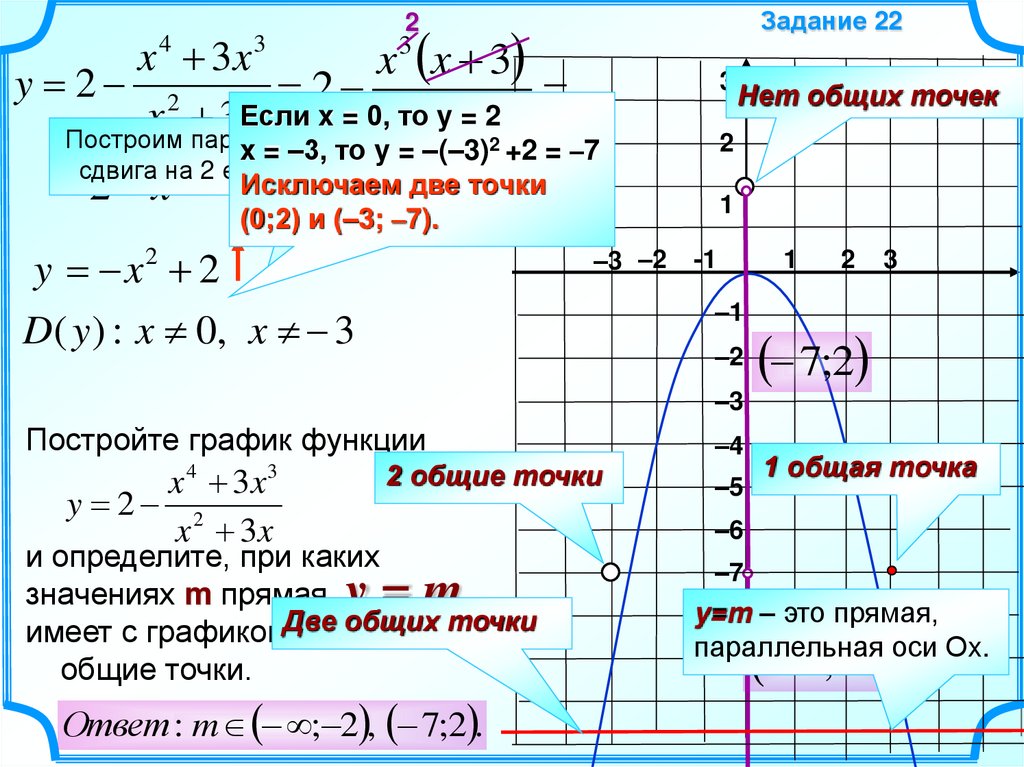
y 2 2
2
Если
x = 0,xто
y
=3
2
x
3
x
x
Построим параболу с помощью
3
2
2 +2 = –7
x = –3, то yx=0,
= –(–3)
x=
-3
сдвига на
2 2 ед. отрезка вверх
Исключаем две точки
2 x
(0;2) и (–3; –7).
y x2 2
D( y ) : x 0, x 3
–3 –2
Нет общих точек
1
-1
–1
–2
–3
Постройте график функции
x 4 3x 3
y 2 2
x 3x
2 общие точки
и определите, при каких
значениях m прямая
общих
имеет с графикомДве
ровно
дветочки
общие точки.
y=m
Ответ : m ; 2 , 7;2 .
–4
–5
1
2
3
7;2
1 общая точка
–6
–7
y=m
–8 – это прямая,
параллельная оси Оx.
; 2
3.
Задание 22x 1 x
y
3x 2 x 1
x 2
x 2
2
При m = 3 прямая проходит
через
проколотую
точкус и
имеет
Построим
параболу
помощью
Используем
формулу для разложения
с параболой
точку.
сдвига наодну
1 ед.общую
отрезок
вниз
квадратного трехчлена на множители
x2 1
2+bx+c=a(x-x )(x-x )
ax
1
2
y x2 1
x 3x 2 0
D( y ) : x 2
x1 x2 3
x = –2, то y = (–2)2 – 1 = 3
Если
общие точки
x1 x2 2 точку (–2;213)!!!
Исключаем
–2
общая точка
x1
1
Постройте
график
функции
3
2
x 1 x 3x 2
y x2 2
2
x 2
y=3
2
1
-1
1
–1
Нет общих точек
и определите,
при
каких
2
x
3xm прямая
2 ( x 1 )( x 2 )
значениях
имеет с графиком ровно одну
( x 1)( x 2)
общую точку.
y = m
2
y= -1
y=m – это прямая,
параллельная
оси Оx.
–2
–3
Ответ: m= –1, m=3.
4.
xy
2
x 6 x x 2
2 Одна общая точка
x 4
2
Используем формулу для разложения
2
квадратного трехчлена на множители
x 2x 3
2+b+c=a(x-x )(x-x )
ax
1
2
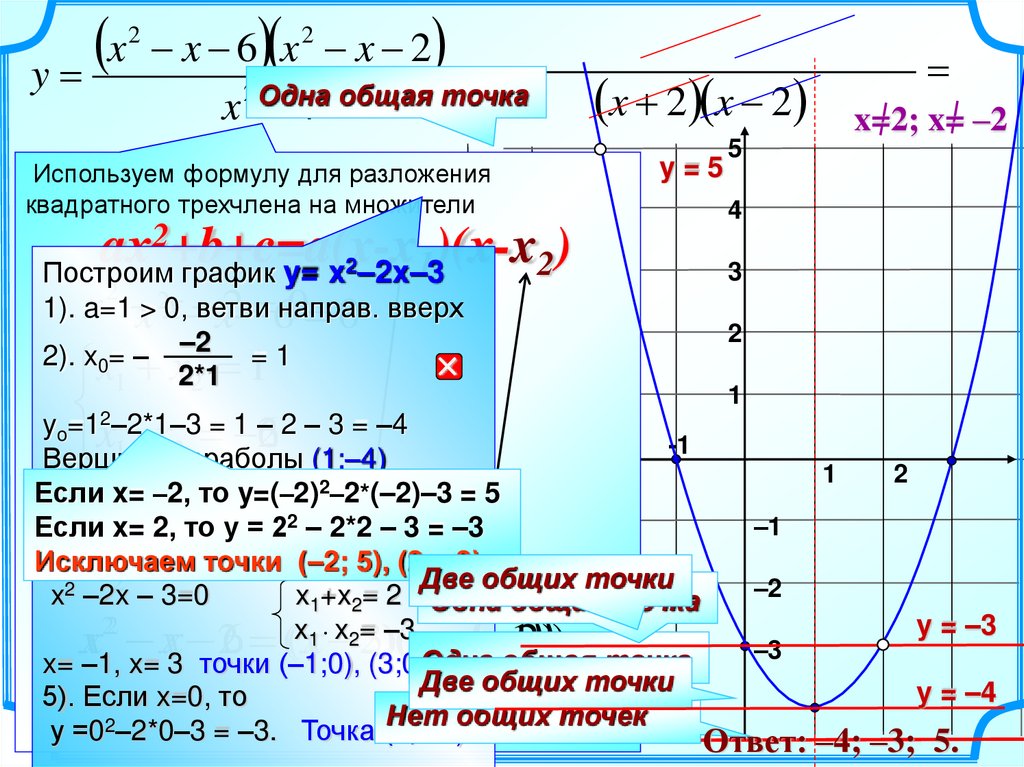
Построим график y= x2–2x–3
1). a=1
x 2 x>2x0, ветви
0 0 вверх
x2 6направ.
y2). x =x – –2
2 x =31
x0 1 x2*1
2 1
2
D( y2) : x 2, x 2.
x 2 x 2
y=5
x=2; x= –2
5
4
3
2
1
yo=1x–2*1–3
=1
–
2 – 3 = –4
x
6
2
-1
–2
2
1 параболы
Вершина
(1;–4)
1
2
Постройте
график
функции
2
Если
3). Ось
x=симметрии
–2,
то y=(
–2)
x =–1.
2*(–2)–3 = 5
2
x
21 3
2
x x=
x2,пересечения
то
6 уx= 22x– 2*2
2с осью
–1
4). Точки
Если
– 3 = –3
y
2точки (–2; 5), (2; –3)
Оx, x
y=0. x2
Исключаем
4
1
Две общих точки
2
2
–2
–2x – 3=0 приxкаких
+x
=
2
и xопределите,
Одна общая точка
1
2
22
y = –3
x1 x2= –3
значениях
m
прямая
x
x
x
x
2
6
(
(
x
x
2
3
)(
x
1
2
)
)
–3
Одна
общая
точка
x=
–1,
x=
3
точки
(–1;0),
(3;0)
имеет с графиком ровно одну
Две общих точки
y = –4
5).общую
Если x=0,
то
(
x
3
)(
x
2
)
точку.
2
1
)
Нет общих точек
у =02–2*0–3 = –3. Точка (0; –3)
Ответ: –4; –3; 5.
y = m
5.
x4 – 13x2 + 36Задание 22 Постройте график функции y =
(x–3)(x+2)
и определите при каких значениях параметра m прямая y = m имеет с
графиком ровно одну общую точку.
x4 – 13x2 + 36 (x–3)(x+3)(x–2)(x+2)
Это приведённое квадратное 2
y=
=
=(x+3)(x–2) = x + x –6
(x–3)(x+2)
(x–3)(x+2)
уравнение (старший
x= коэффициент
3
x= –2 равен 1).
Пусть x2 = t
Найдем корни по теореме Виета.
t2 – 13t + 36 = 0
t1 + t2 = 13
t1 = 9
t1 t2 = 36
t2 = 4
Разложим трёхчлен на множители
по формуле
a(x – x1)(x –y x2)
5
t2 – 13t + 36 = (t – 9)(t – 4) = (x2 – 9)(x2 – 4) = (x–3)(x+3)(x–2)(x+2)
Вернёмся
двучлены
Построим график функции
y = x2 к+замене,
x –6 разложим
ГОТОВИМСЯ
2 – b2 = (a – b)(a+b)
по
формуле
a
D(y): x= 3,
x= –2
x
К
ОГЭ
6.
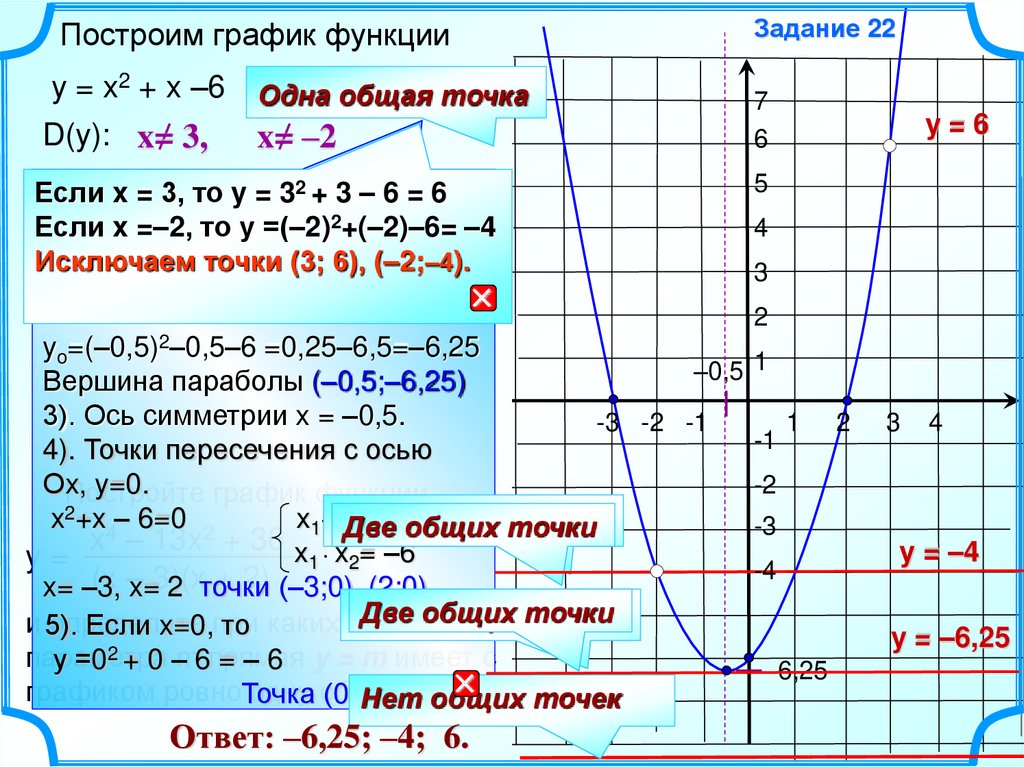
Построим график функцииy = x2 + x –6
Одна общая точка
D(y): x= 3,
x= –2
2 + 32 – 6 = 6
Если
x = 3,график
то y = 3y=
Построим
x +x–6
2+(–2)–6= –4
Если
x =–2,
то у =(–2)
1). a=1
> 0, ветви
направ.
вверх
Исключаем1точки (3; 6), (–2;–4).
2). x0= –
= –0,5
2*1
yo=(–0,5)2–0,5–6 =0,25–6,5=–6,25
–0,5
Вершина параболы (–0,5;–6,25)
3). Ось симметрии x = –0,5.
-3 -2 -1
4). Точки пересечения с осью
Оx,
y=0.
Постройте
график функции
2
x +x4– 6=0 2
x1+x
Одна
общая точка
2= –1
Две
x – 13x + 36 x x = –6общих точки
y=
1
2
(x
–
3)(x
+
2)
x= –3, x= 2 точки (–3;0), (2;0)
Две общих
Одна
общаяточки
точка
и 5).
определите
Если x=0,при
то каких значениях
параметра
у =02 + 0 –m6прямая
= – 6 y = m имеет с
графиком ровноТочка
одну общую
(0; Нет
–6) точку.
общих точек
Ответ: –6,25; –4; 6.
Задание 22
7
6
y=6
5
4
3
2
1
-1
1
2
3
4
-2
-3
-4
y = –4
y = –6,25
–6,25
7.
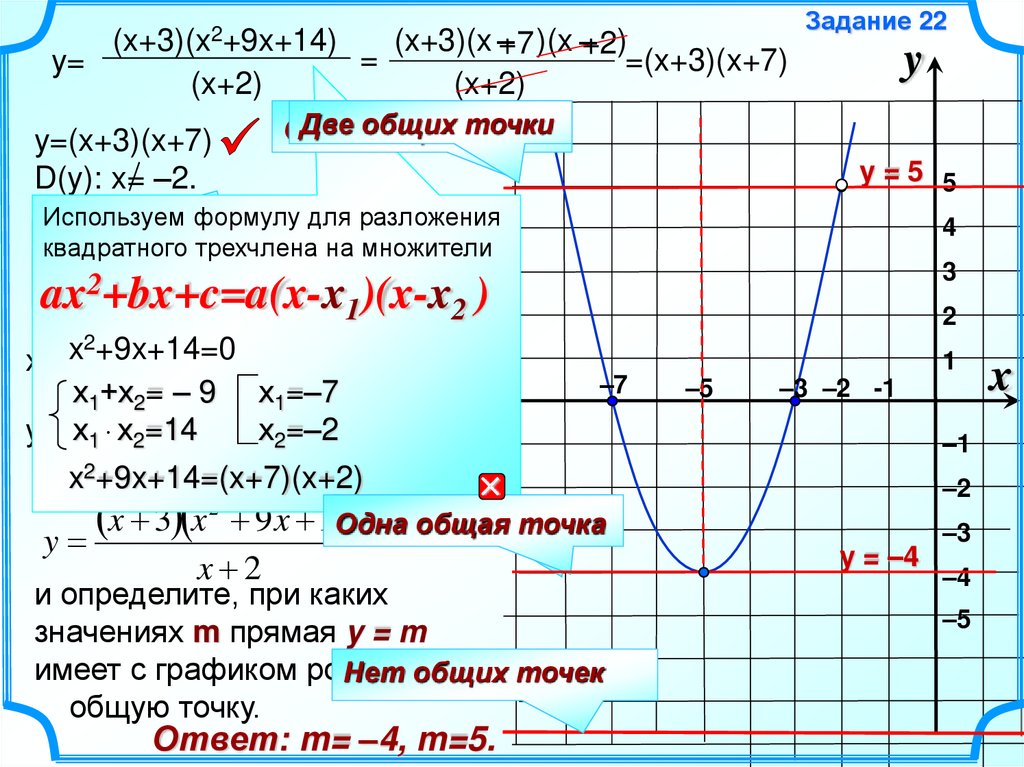
y=(x+3)(x2+9x+14)
(x+2)
y=(x+3)(x+7)
D(y): x= –2.
=
(x+3)(x –+7 )(x –+2)
=(x+3)(x+7)
(x+2)
x 3 x
y
y
Две общих
Одна
общая точки
точка
y=5 5
Используем формулу для разложения
Найдем
нули
функции –2+7)=5
Если
x=–2, трехчлена
то y=(–2+3)(
квадратного
на множители
(x+3)(x+7)=0
Исключаем точку (–2; 5)
2
ax–3,+bx+c=a(x-x
x=
x= –7.
1)(x-x2 )
2+9x+14=0
–7+(–3)
x
Вершина
x0=
= –5
(–5;–4)
х1+х22=
-2 – 9 2 х1=–7
х1 х2=14
х2=–2
y(–5)=(-5+3)(-5+7)
=–4
Постройте
x2+9x+14=(x+7)(x+2)
график функции
4
3
2
–7
Две общих
9 x 14
Одна
общаяточки
точка
x 2
2
Задание 22
и определите, при каких
значениях m прямая y = m
имеет с графиком ровно
Нетодну
общих точек
общую точку.
Ответ: m= –4, m=5.
–5
–3 –2 -1
1
–1
–2
y = –4
–3
–4
–5
x
8.
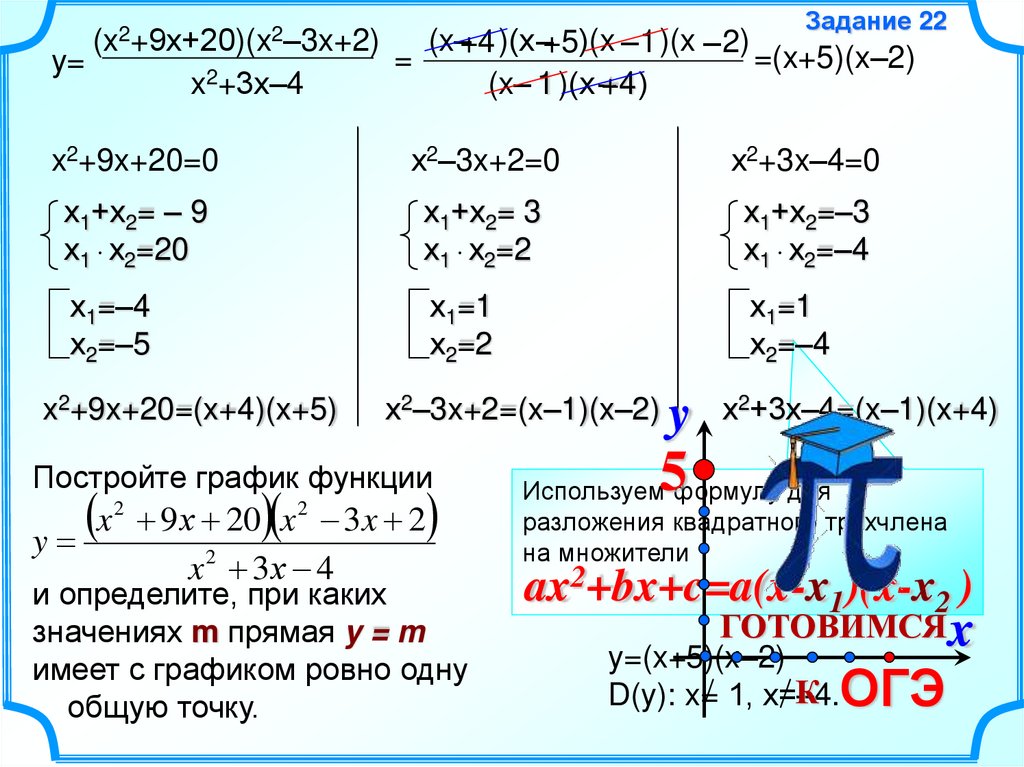
y=(x2+9х+20)(x2–3x+2)
x2+3х–4
Задание 22
(x–+4 )(х –+5)(x – 1 )(x – 2)
=(x+5)(x–2)
(x– 1 )(х –+4 )
=
x2+9x+20=0
х2–3x+2=0
х2+3x–4=0
х1+х2= – 9
х1 х2=20
х1+х2= 3
х1 х2=2
х1+х2=–3
х1 х2=–4
х1=–4
х2=–5
х1=1
х2=2
х1=1
х2=–4
x2+9x+20=(x+4)(x+5)
х2–3x+2=(x–1)(x–2)
Постройте график функции
x
y
2
9 х 20 x 2 3x 2
x 2 3х 4
и определите, при каких
значениях m прямая y = m
имеет с графиком ровно одну
общую точку.
y
х2+3х–4=(x–1)(x+4)
5
Используем формулу для
разложения квадратного трехчлена
на множители
ax2+bx+c=a(x-x1)(x-x2 )
ГОТОВИМСЯ x
y=(x+5)(x–2)
К
D(y): x= 1, х=–4.
ОГЭ
9.
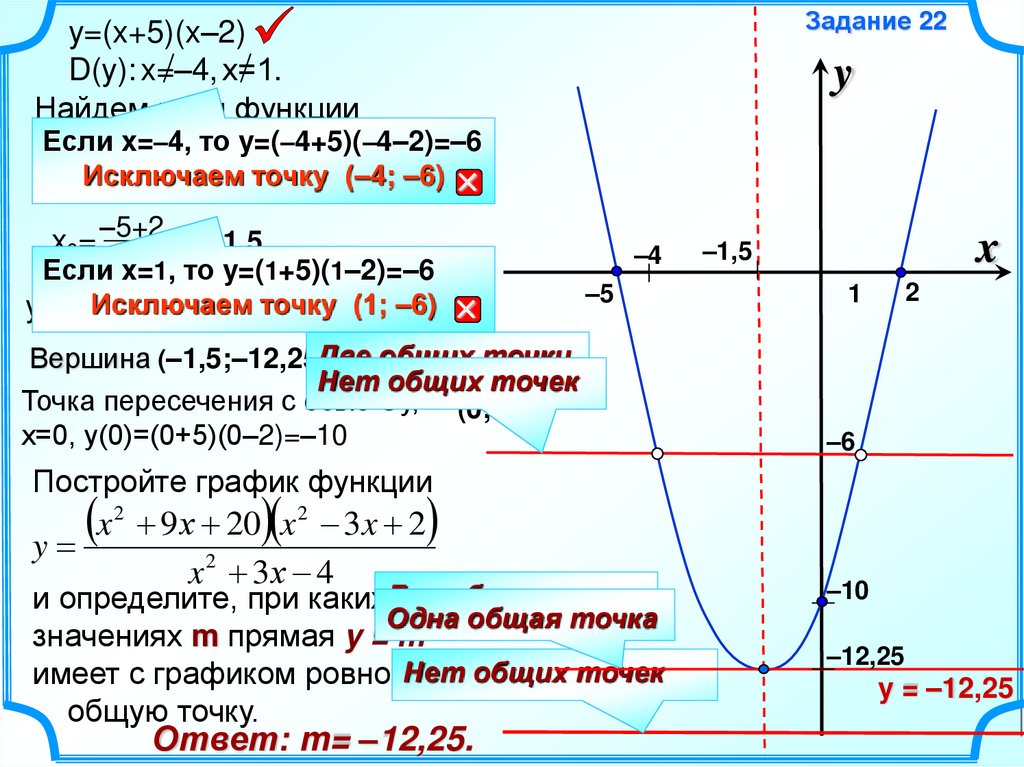
Задание 22y=(x+5)(x–2)
D(y): x=–4, х=1.
Найдем нули функции
Если
x=–4, то y=(–4+5)(–4–2)=–6
(x+5)(x–2)=0
Исключаем
точку (–4; –6)
x= –5,
x= 2.
y
x0= –5+2 = –1,5
2 1, то y=(1+5)(1–2)=–6
Если x=
3,5
-3,5
Исключаем точку (1;
–6)
y(–1,5)=(-1,5+5)(-1,5-2)
=–12,25
–4
–5
Вершина (–1,5;–12,25)Две общих точки
Нет общих точек
Точка пересечения с осью Оу, (0;–10)
х=0, у(0)=(0+5)(0–2)=–10
x
–1,5
2
1
–6
Постройте график функции
x
y
2
9 х 20 x 2 3x 2
x 2 3х 4
и определите, при какихДве общих точки
Одна общая точка
значениях m прямая y = m
Нет общих точек
имеет с графиком ровно одну
общую точку.
Ответ: m= –12,25.
–10
–12,25
y = –12,25


 Математика
Математика








