Прямая. Часть II

1.

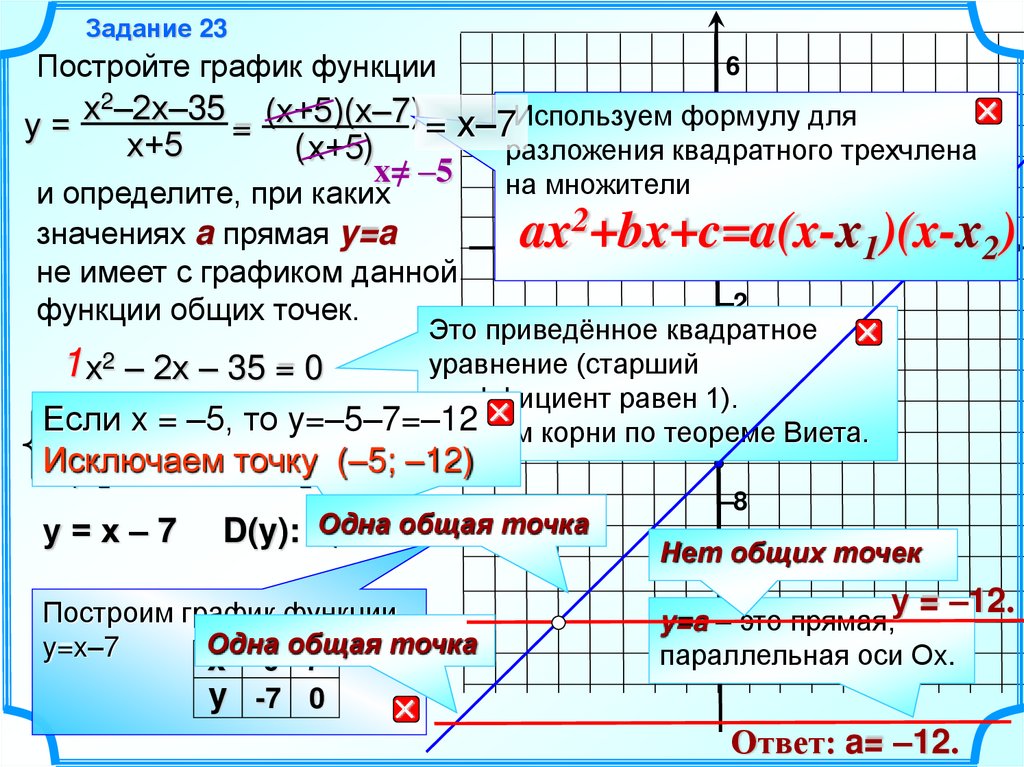
Задание 23
Постройте график функции
6
не имеет с графиком данной
функции общих точек.
–2
2–2х–35
х
(х+5)(х–7) = х–7Используем формулу
для
4
у=
=
х+5
( х+5)
разложения квадратного трехчлена
x= –5
на множители 2
и определите, при каких
значениях a прямая y=a
ax2+bx+c=a(x-x1)(x-x2)
-5
-3 -1
1
3
5
7
Это приведённое квадратное
уравнение (старший –4
1 х2 – 2х – 35 = 0
коэффициент
равен 1).
Если
x1+х2x==2–5, то xy=–5–7=–12
–6 Виета.
1= –5
Найдем корни по теореме
Исключаем
x1х2 =– 35 точку
х2 =(–5;
7 –12)
у=х–7
Одна
D(y): x=
–5 общая точка
Построим график функции
Одна общая точка
y=x–7
x 0 7
y -7 0
–8
Нет–10
общих точек
у = –12.
y=a ––12
это прямая,
параллельная оси Оx.
Ответ: a= –12.

2.

Постройте график функции
2
( x2–4 )
y=
x–2
y
5
x
ОГЭ
a
2
( a
= –a
2
)
=a
и определите, при
каких значениях a
прямая y=a не имеет с
графиком данной
функции общих точек.

3.

x 4 x 4 ( x 2)( x 2) = x + 2
y
2
2
2
x 2
Задание 23
x 2
x 2
D(y): x2 – 4 > 0, x = 2;
(x–2)(x+2) > 0,
–
+
Одна общая точка
+
–2
2
8
8
;–2], ( 2; + Нет
) общих точек
D(y): (–
1
y = x+ 2
Постройте график функции
y
у=4
4
4 x
x 2
-2 -1
у=0
1 2 3 4
–2
2
Одна общая точка
Найдите значения a, при
которых прямая y=a не имеет
с графиком данной функции
общих точек.
Ответ: (0; 4].
–4