Гипербола с проколотой точкой. Часть II

1.

4x 8
4
4( x 2)
y 2
x 2x
x
x( x 2)
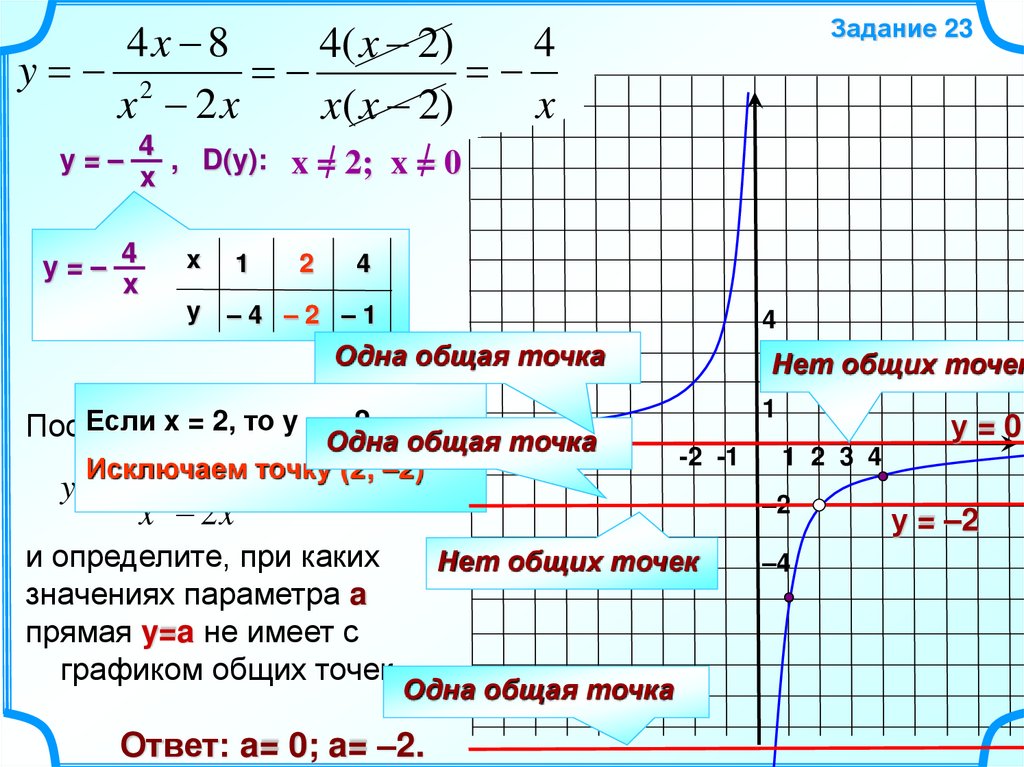
Задание 23
y = – 4 , D(y): x = 2; x = 0
x
y=– 4
x
x
1
2
4
y –4 –2 –1
4
Одна общая точка
Если x =
2, то y функции
=–2
Постройте
график
Одна общая точка
4 x 8 точку (2; –2)
Исключаем
y
Нет общих точек
1
-2 -1
x2 2x
у=0
1 2 3 4
–2
и определите, при каких
значениях параметра a
прямая y=a не имеет с
графиком общих точек.
Нет общих точек
Одна общая точка
Ответ: a= 0; a= –2.
–4
у = –2

2.

4x 2
2
2 2 x 1
y 2
2x x
x
x 2 x 1
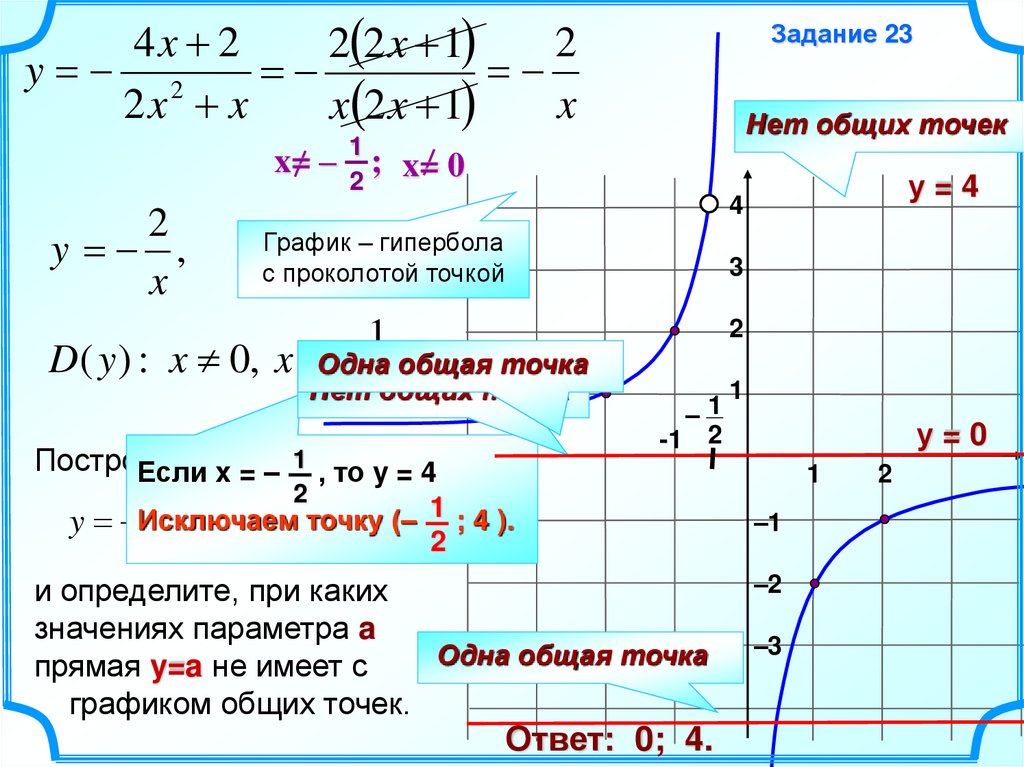
Задание 23
Нет общих точек
x= – 1 ; x= 0
2
2
y ,
x
у=4
4
График – гипербола
с проколотой точкой
3
1
D ( y ) : x 0, x Одна
общая точка
Нет2общих точек
Постройте
Еслиграфик
x = – 1 функции
, то y = 4
2
–1
-1 2
2
4x 2
1 ; 4 ).
точку
(–
y Исключаем
2
2x2 x
и определите, при каких
значениях параметра a
Одна общая точка
прямая y=a не имеет с
графиком общих точек.
Ответ: 0; 4.
1
у=0
1
–1
–2
–3
2

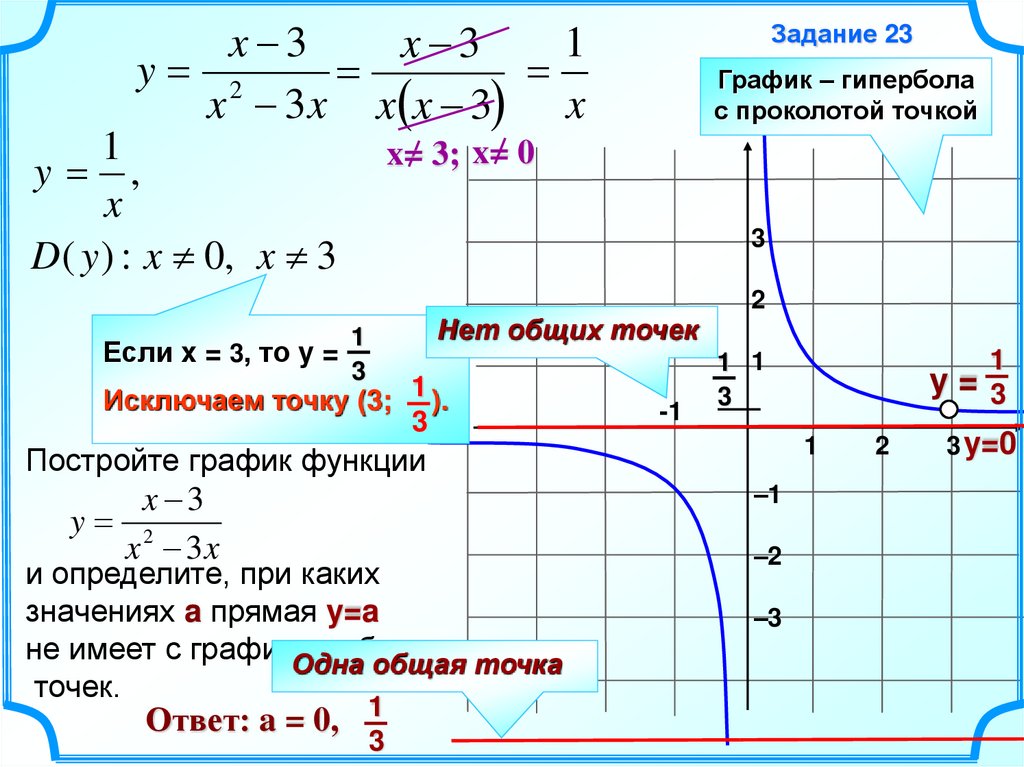
3.

x 3
1
x 3
y 2
x 3 x x x 3 x
1
y ,
x
D ( y ) : x 0, x 3
Задание 23
График – гипербола
с проколотой точкой
x= 3; x= 0
3
Нет общих точек
1
Если x = 3, то y =
3
Исключаем точку (3; 1 ).
3
-1
2
–1
и определите, при каких
значениях a прямая y=a
не имеет с графиком
общих
Одна общая точка
точек.
Ответ: a = 0, 1
3
y=3
1
Постройте график функции
x 3
y 2
x 3x
1
1 1
3
–2
–3
2
3 y=0

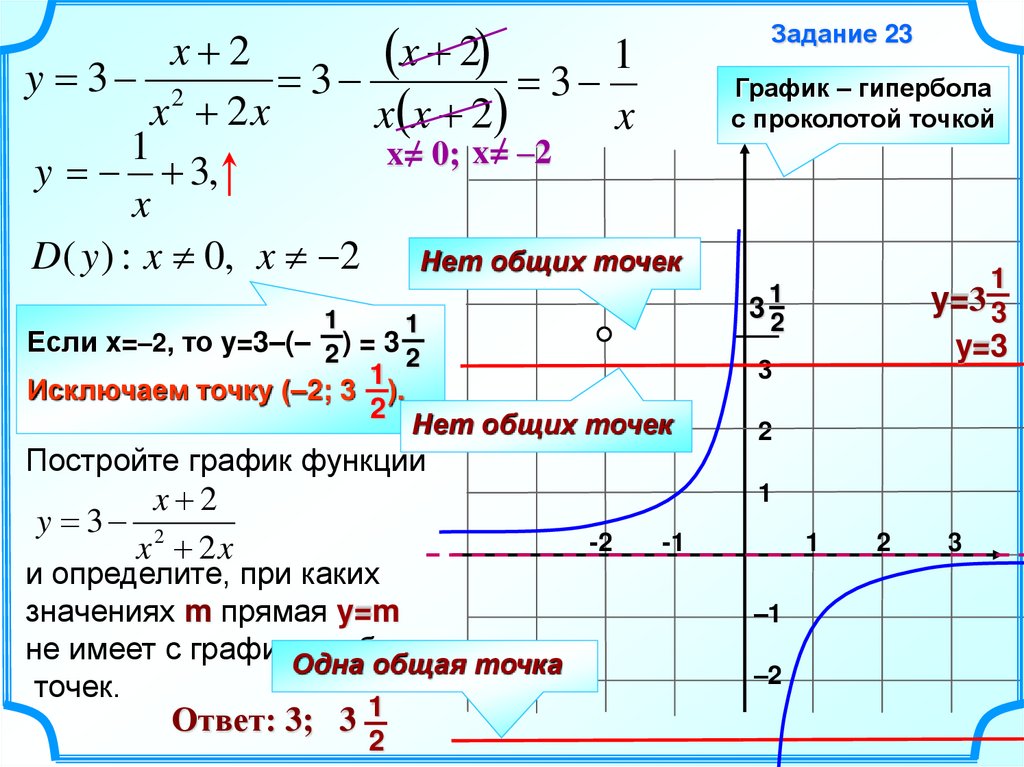
4.

x 2
x 2
1
y 3 2
3
3
x 2x
x x 2
x
1
x= 0; x= –2
y 3,
x
D ( y ) : x 0, x 2 Нет общих точек
1
y=3 3
y=3
3
Нет общих точек
Постройте график функции
x 2
y 3 2
x 2x
График – гипербола
с проколотой точкой
1
32
1
1
Если x=–2, то y=3–(– 2 ) = 3
2
1
Исключаем точку (–2; 3 ).
2
Задание 23
2
1
и определите, при каких
значениях m прямая y=m
не имеет с графиком
общих
Одна общая точка
точек.
Ответ: 3; 3 1
2
-2
-1
1
–1
–2
2
3

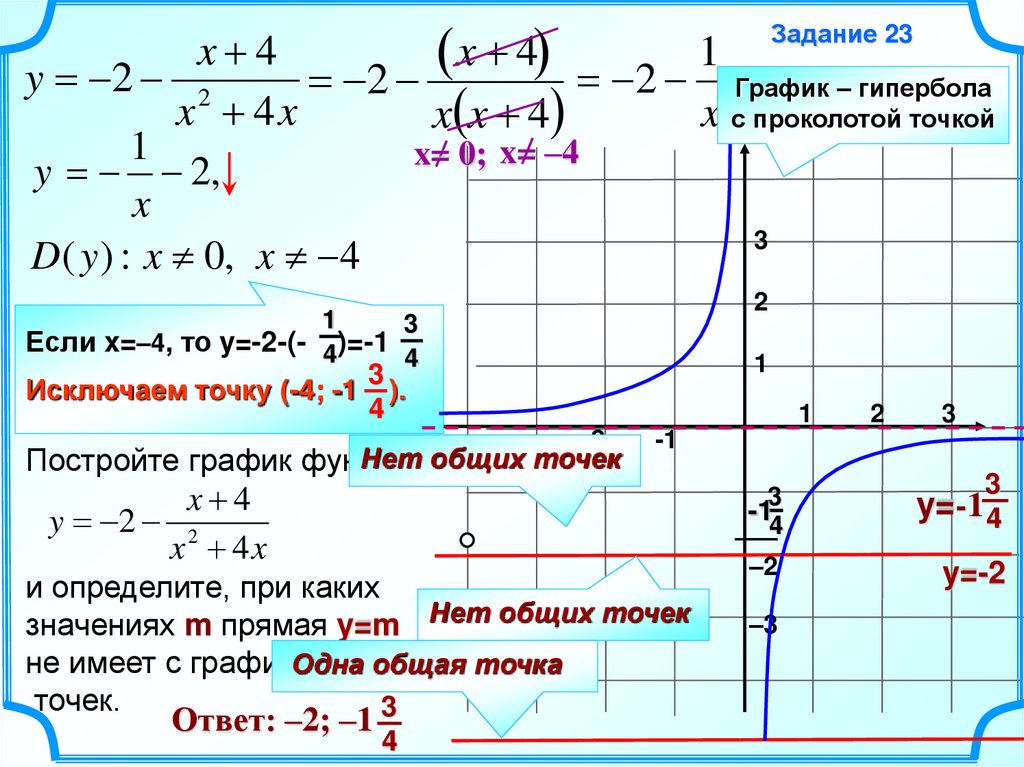
5.

x 4
1
x 4
y 2 2
2 График – гипербола
2
x 4x
x с проколотой точкой
x x 4
1
x= 0; x= –4
y 2,
x
3
D ( y ) : x 0, x 4
Задание 23
2
1
3
Если x=–4, то y=-2-(- 4)=-1
4
1
3
Исключаем точку (-4; -1 ).
4
1
-2
Нет общих точек
Постройте график функции
и определите, при каких
значениях m прямая y=m Нет общих точек
не имеет с графиком
общих
Одна
общая точка
точек.
3
4
3
-1
x 4
y 2 2
x 4x
Ответ: –2; –1
2
3
-14
3
y=-1 4
–2
y=-2
–3

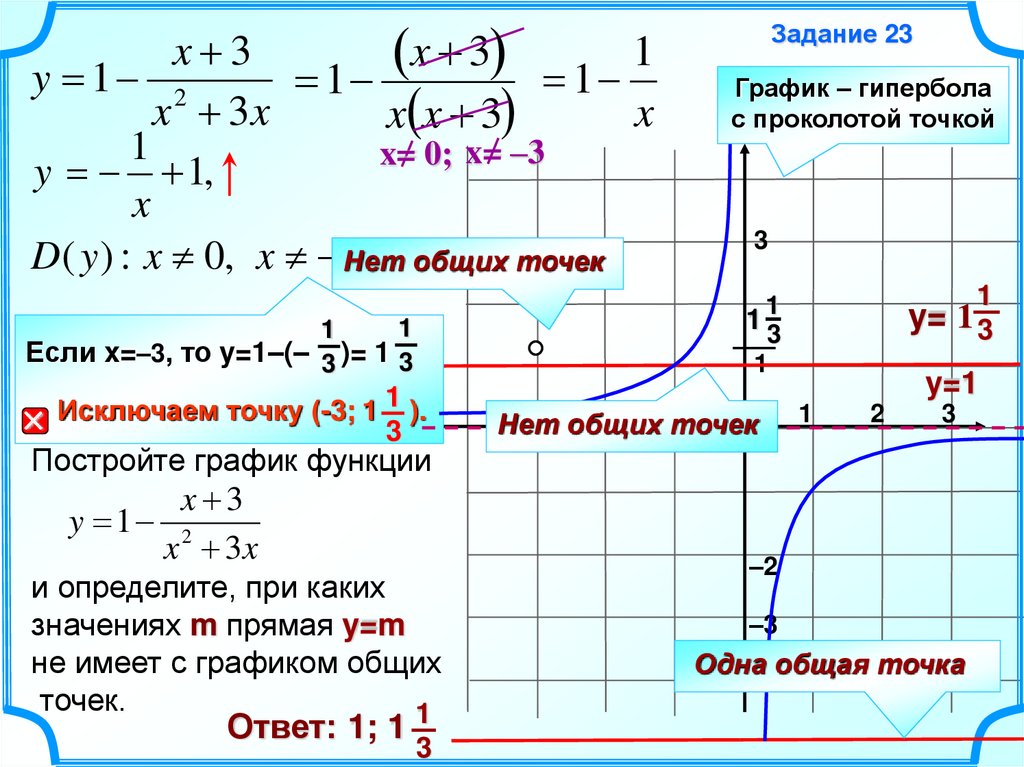
6.

x 3
1
x 3
y 1 2
1
1
x 3x
x
x x 3
1
x= 0; x= –3
y 1,
x
D ( y ) : x 0, x 3Нет общих точек
Задание 23
График – гипербола
с проколотой точкой
3
1
1
Если x=–3, то y=1–(– 3 )= 1 3
Исключаем точку (-3; 1 1 ).
3
Постройте график функции
x 3
y 1 2
x 3x
и определите, при каких
значениях m прямая y=m
не имеет с графиком общих
точек.
1
Ответ: 1; 1
1
y= 1 3
1
13
1
3
Нет общих точек
-2
y=1
1
2
3
-1
–2
–3
Одна общая точка

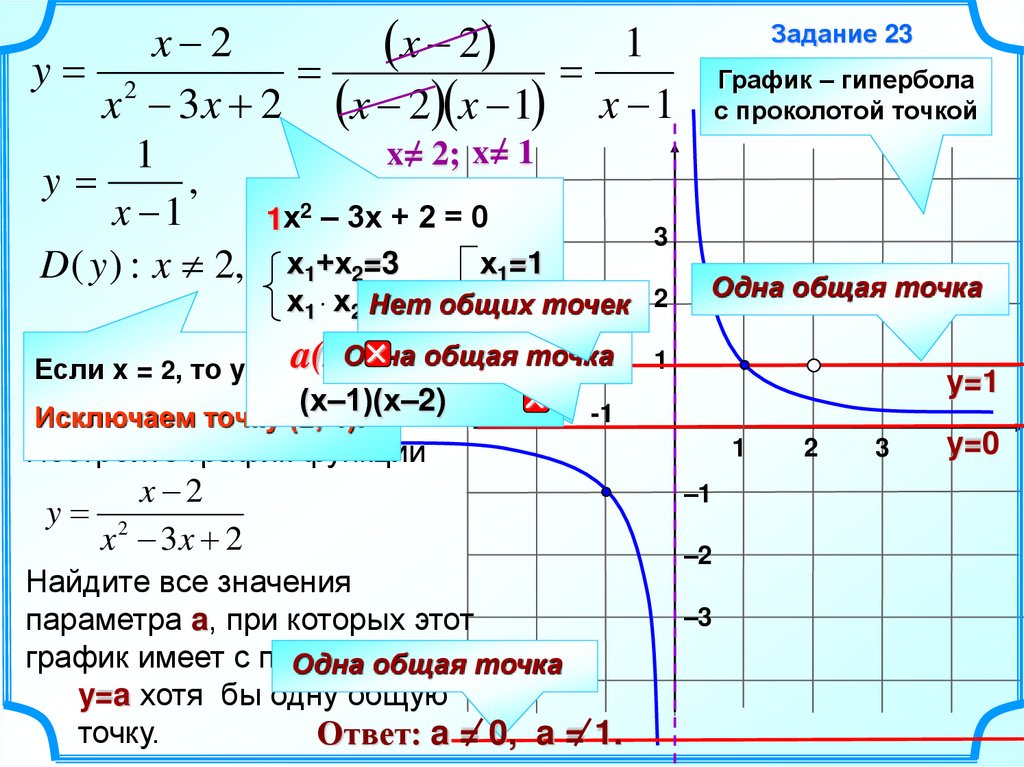
7.

x 2
1
x 2
y 2
x 3x 2 x 2 x 1 x 1
x= 2; x= 1
1
y
,
x 1
1х2 – 3х + 2 = 0
х1=1
D ( y ) : x 2, x х 1+х
1 2=3
1)(x–x
1
Одна
Нет
общих
общая
точка
a(x–x
1) точек
=1
2-1
(х–1)(х–2)
-1
Исключаем точку (2; 1).
График – гипербола
с проколотой точкой
3
х1 х2=2
х2=2точек 2
Нет общих
Если x = 2, то y =
Задание 23
Одна общая точка
1
y=1
Постройте график функции
y
x 2
x 2 3x 2
Найдите все значения
параметра a, при которых этот
график имеет с прямой
Одна общая точка
y=a хотя бы одну общую
точку.
Ответ: a = 0, a = 1.
1
–1
–2
–3
2
3
y=0

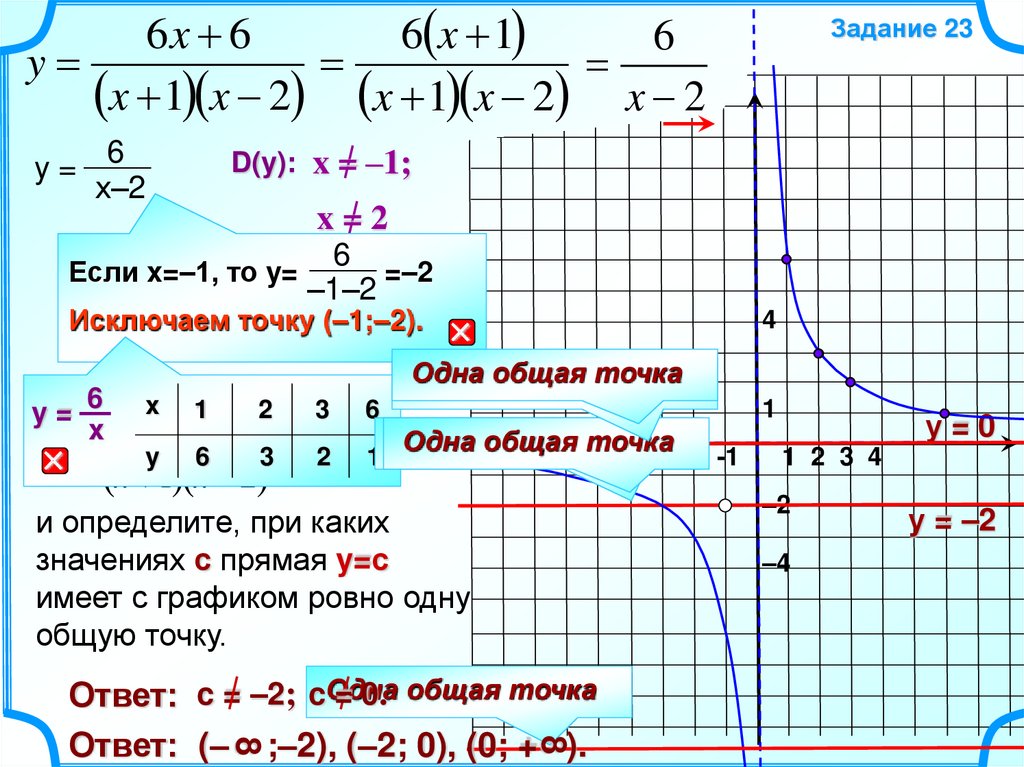
8.

6x 6
6 x 1
6
y
x 1 x 2 x 1 x 2 x 2
y=
6
х–2
Задание 23
D(y): x = –1;
x=2
Если x=–1, то y=
6
=–2
–1–2
Исключаем точку (–1;–2).
4
Одна общая точка
Нет общих точек
Постройте
6 x график функции
y=
1
2
6x 6
y x y1 x6 2 3
x
3
2
1
6
1
Нет
Одна
общих
общая
точек
точка
-2 -1
у=0
1 2 3 4
–2
и определите, при каких
значениях с прямая y=с
имеет с графиком ровно одну
общую точку.
–4
8
8
= 0. общая точка
Ответ: c = –2; cОдна
Ответ: (– ;–2), (–2; 0), (0; + ).
у = –2

9.

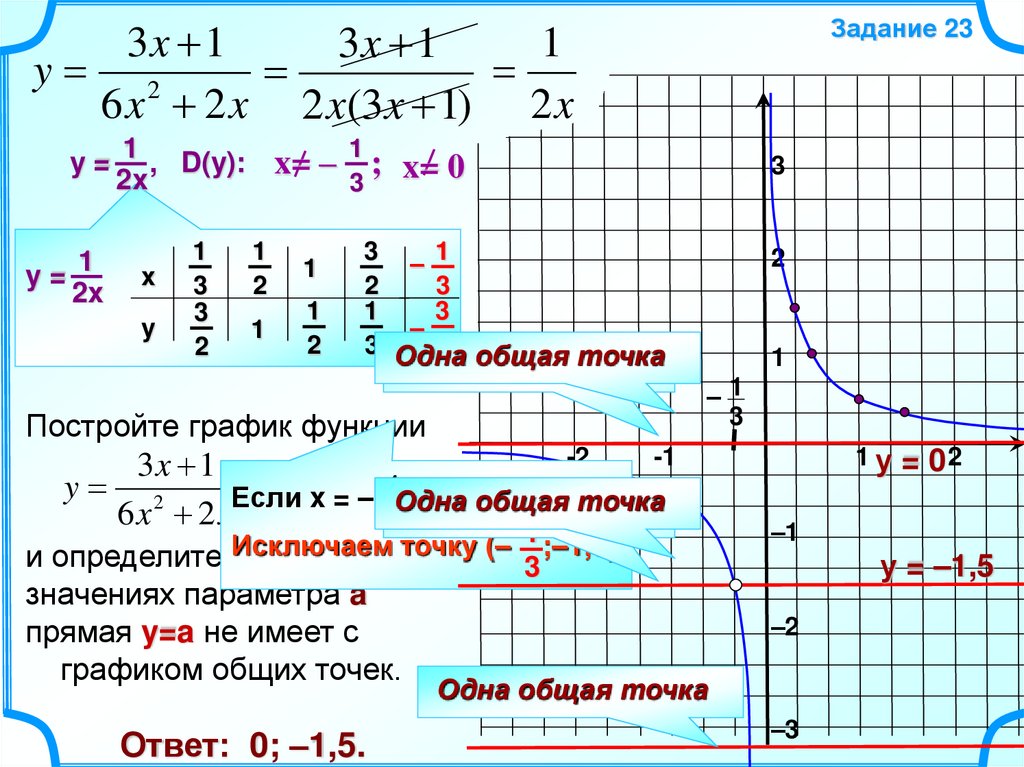
3x 1
1
3x 1
y 2
6 x 2 x 2 x(3x 1) 2 x
Задание 23
1
y = 1 , D(y): x= – ; x= 0
2x
3
y= 1
2x
x
y
1
3
3
2
1
2
1
1
1
2
3 – 1
3
2
3
1
–
2 общая точка
3 Одна
Нет общих
точек
Постройте график функции
3
2
1
–1
3
-2
-1
3x 1
y 2
Если x = – 1Одна
, то yобщая
=– 1,5 точка
6x 2x
3Нет общих точек
1 ;–1,5)
Исключаем
точку
(–
и определите, при каких
3
значениях параметра a
прямая y=a не имеет с
графиком общих точек.
Ответ: 0; –1,5.
1у
= 02
–1
у = –1,5
–2
Одна общая точка
–3

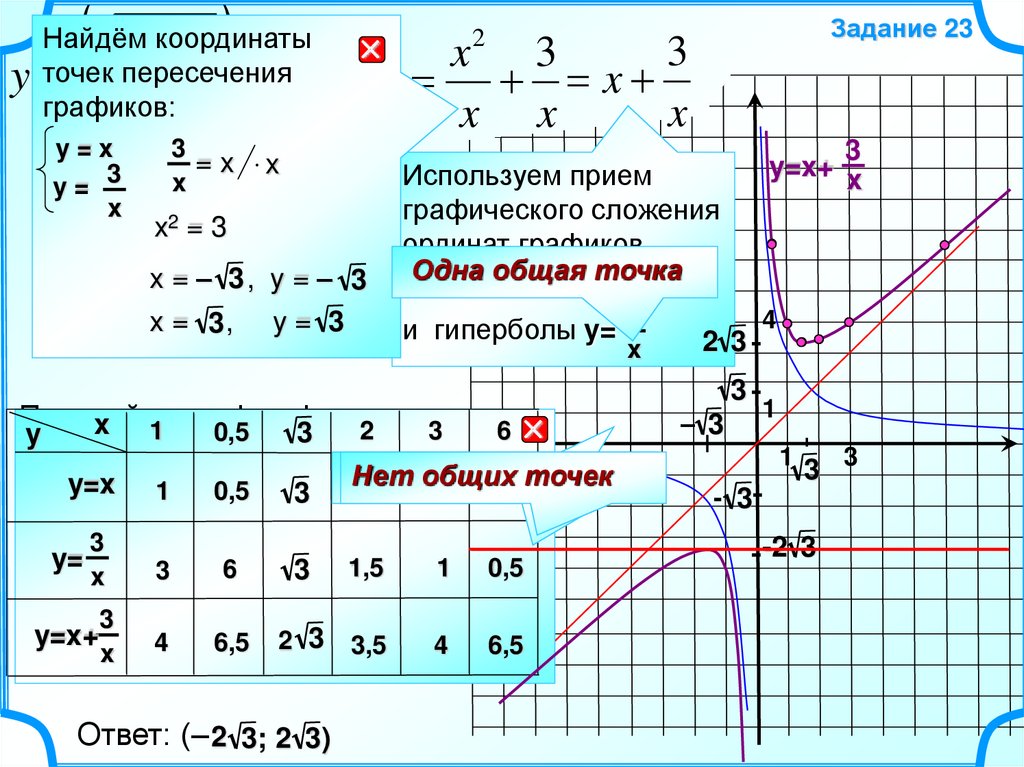
10.

y
y=x
D(y):
x32 +
= 3x > 0,
x
2 координаты
2
2
Найдём
x
3
x 3
точек пересечения
графиков:
x
x
y = 3Верноxпри любом x
x
2
x = 0;
x =3
x = – 3, y = – 3
x = 3, y = 3
3
x 3
x
x
x x
x 3
y=x
y
1
x
2
0,5
3
и гиперболы y=
3
3
Найдите
значения a, при
y=
1
6
3 1,5
3
x
которых
прямая y=a не имеет
3
сy=x+
графиком
данной 3функции
4
6,5 2
3,5
4
x точек.
общих
Ответ: (– 2 3; 2 3)
6
Одна
Нет общих
общаяточек
точка
2
3
y=x+ x
Используем прием
графического сложения
ординат графиков
Однапрямой
общая y=x
точка
Постройте
функции
x 1 график
2
3
0,5
3
y
2
Задание 23
2
6
0,5
6,5
3
x
2 3
3
– 3
4
1
1
3 3
- 3
-2 3